A Poisson Process AutoDecoder for X-ray Sources

X-ray observing facilities, such as the Chandra X-ray Observatory and the eROSITA, have detected millions of astronomical sources associated with high-energy phenomena. The arrival of photons as a function of time follows a Poisson process and can vary by orders-of-magnitude, presenting obstacles for common tasks such as source classification, physical property derivation, and anomaly detection. Previous work has either failed to directly capture the Poisson nature of the data or only focuses on Poisson rate function reconstruction. In this work, we present Poisson Process AutoDecoder (PPAD). PPAD is a neural field decoder that maps fixed-length latent features to continuous Poisson rate functions across energy band and time via unsupervised learning. PPAD reconstructs the rate function and yields a representation at the same time. We demonstrate the efficacy of PPAD via reconstruction, regression, classification and anomaly detection experiments using the Chandra Source Catalog.

Multi-student Diffusion Distillation for Better One-step Generators

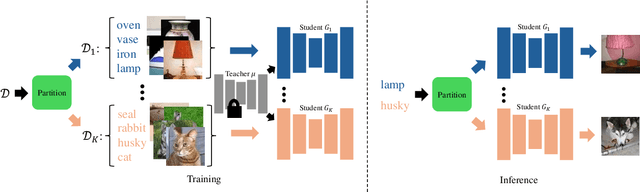
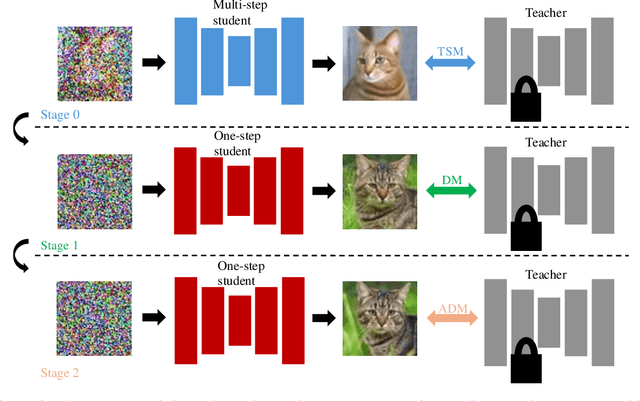
Diffusion models achieve high-quality sample generation at the cost of a lengthy multistep inference procedure. To overcome this, diffusion distillation techniques produce student generators capable of matching or surpassing the teacher in a single step. However, the student model's inference speed is limited by the size of the teacher architecture, preventing real-time generation for computationally heavy applications. In this work, we introduce Multi-Student Distillation (MSD), a framework to distill a conditional teacher diffusion model into multiple single-step generators. Each student generator is responsible for a subset of the conditioning data, thereby obtaining higher generation quality for the same capacity. MSD trains multiple distilled students, allowing smaller sizes and, therefore, faster inference. Also, MSD offers a lightweight quality boost over single-student distillation with the same architecture. We demonstrate MSD is effective by training multiple same-sized or smaller students on single-step distillation using distribution matching and adversarial distillation techniques. With smaller students, MSD gets competitive results with faster inference for single-step generation. Using 4 same-sized students, MSD sets a new state-of-the-art for one-step image generation: FID 1.20 on ImageNet-64x64 and 8.20 on zero-shot COCO2014.

Generalization error of min-norm interpolators in transfer learning

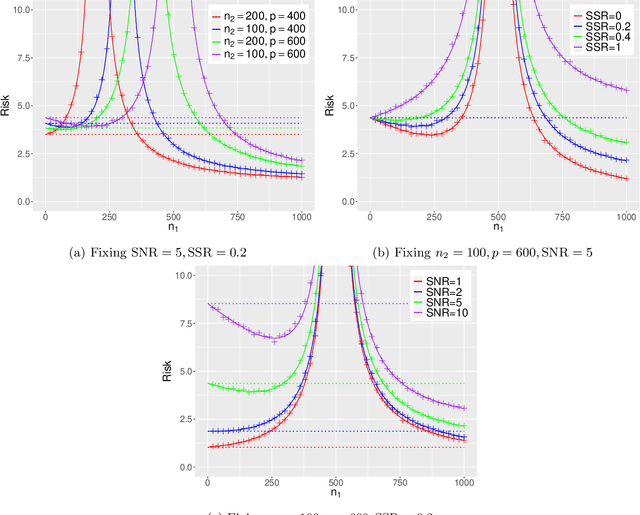
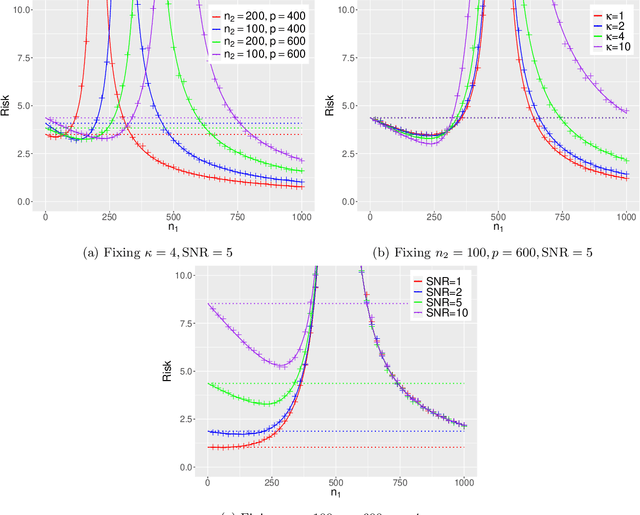
This paper establishes the generalization error of pooled min-$\ell_2$-norm interpolation in transfer learning where data from diverse distributions are available. Min-norm interpolators emerge naturally as implicit regularized limits of modern machine learning algorithms. Previous work characterized their out-of-distribution risk when samples from the test distribution are unavailable during training. However, in many applications, a limited amount of test data may be available during training, yet properties of min-norm interpolation in this setting are not well-understood. We address this gap by characterizing the bias and variance of pooled min-$\ell_2$-norm interpolation under covariate and model shifts. The pooled interpolator captures both early fusion and a form of intermediate fusion. Our results have several implications: under model shift, for low signal-to-noise ratio (SNR), adding data always hurts. For higher SNR, transfer learning helps as long as the shift-to-signal (SSR) ratio lies below a threshold that we characterize explicitly. By consistently estimating these ratios, we provide a data-driven method to determine: (i) when the pooled interpolator outperforms the target-based interpolator, and (ii) the optimal number of target samples that minimizes the generalization error. Under covariate shift, if the source sample size is small relative to the dimension, heterogeneity between between domains improves the risk, and vice versa. We establish a novel anisotropic local law to achieve these characterizations, which may be of independent interest in random matrix theory. We supplement our theoretical characterizations with comprehensive simulations that demonstrate the finite-sample efficacy of our results.