Pragya Sur
Preventing Model Collapse Under Overparametrization: Optimal Mixing Ratios for Interpolation Learning and Ridge Regression
Sep 26, 2025Abstract:Model collapse occurs when generative models degrade after repeatedly training on their own synthetic outputs. We study this effect in overparameterized linear regression in a setting where each iteration mixes fresh real labels with synthetic labels drawn from the model fitted in the previous iteration. We derive precise generalization error formulae for minimum-$\ell_2$-norm interpolation and ridge regression under this iterative scheme. Our analysis reveals intriguing properties of the optimal mixing weight that minimizes long-term prediction error and provably prevents model collapse. For instance, in the case of min-$\ell_2$-norm interpolation, we establish that the optimal real-data proportion converges to the reciprocal of the golden ratio for fairly general classes of covariate distributions. Previously, this property was known only for ordinary least squares, and additionally in low dimensions. For ridge regression, we further analyze two popular model classes -- the random-effects model and the spiked covariance model -- demonstrating how spectral geometry governs optimal weighting. In both cases, as well as for isotropic features, we uncover that the optimal mixing ratio should be at least one-half, reflecting the necessity of favoring real-data over synthetic. We validate our theoretical results with extensive simulations.
GLAMP: An Approximate Message Passing Framework for Transfer Learning with Applications to Lasso-based Estimators
May 28, 2025Abstract:Approximate Message Passing (AMP) algorithms enable precise characterization of certain classes of random objects in the high-dimensional limit, and have found widespread applications in fields such as statistics, deep learning, genetics, and communications. However, existing AMP frameworks cannot simultaneously handle matrix-valued iterates and non-separable denoising functions. This limitation prevents them from precisely characterizing estimators that draw information from multiple data sources with distribution shifts. In this work, we introduce Generalized Long Approximate Message Passing (GLAMP), a novel extension of AMP that addresses this limitation. We rigorously prove state evolution for GLAMP. GLAMP significantly broadens the scope of AMP, enabling the analysis of transfer learning estimators that were previously out of reach. We demonstrate the utility of GLAMP by precisely characterizing the risk of three Lasso-based transfer learning estimators: the Stacked Lasso, the Model Averaging Estimator, and the Second Step Estimator. We also demonstrate the remarkable finite sample accuracy of our theory via extensive simulations.
Optimal and Provable Calibration in High-Dimensional Binary Classification: Angular Calibration and Platt Scaling
Feb 21, 2025Abstract:We study the fundamental problem of calibrating a linear binary classifier of the form $\sigma(\hat{w}^\top x)$, where the feature vector $x$ is Gaussian, $\sigma$ is a link function, and $\hat{w}$ is an estimator of the true linear weight $w^\star$. By interpolating with a noninformative $\textit{chance classifier}$, we construct a well-calibrated predictor whose interpolation weight depends on the angle $\angle(\hat{w}, w_\star)$ between the estimator $\hat{w}$ and the true linear weight $w_\star$. We establish that this angular calibration approach is provably well-calibrated in a high-dimensional regime where the number of samples and features both diverge, at a comparable rate. The angle $\angle(\hat{w}, w_\star)$ can be consistently estimated. Furthermore, the resulting predictor is uniquely $\textit{Bregman-optimal}$, minimizing the Bregman divergence to the true label distribution within a suitable class of calibrated predictors. Our work is the first to provide a calibration strategy that satisfies both calibration and optimality properties provably in high dimensions. Additionally, we identify conditions under which a classical Platt-scaling predictor converges to our Bregman-optimal calibrated solution. Thus, Platt-scaling also inherits these desirable properties provably in high dimensions.
Generalization error of min-norm interpolators in transfer learning
Jun 20, 2024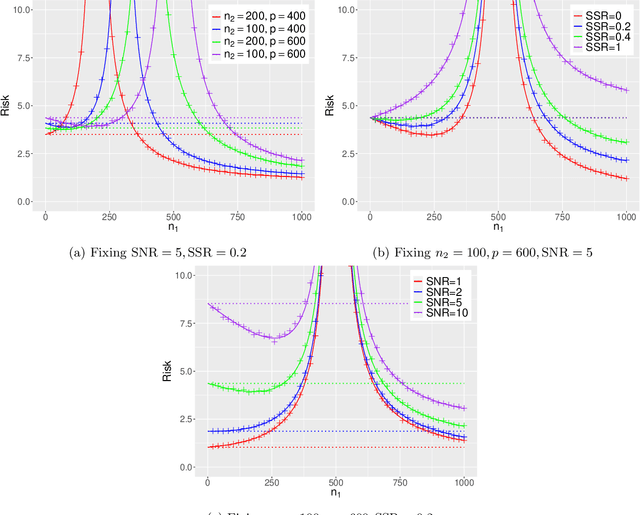
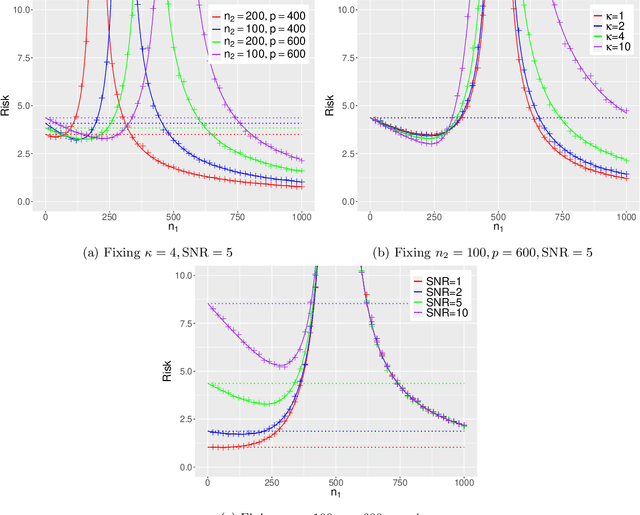
Abstract:This paper establishes the generalization error of pooled min-$\ell_2$-norm interpolation in transfer learning where data from diverse distributions are available. Min-norm interpolators emerge naturally as implicit regularized limits of modern machine learning algorithms. Previous work characterized their out-of-distribution risk when samples from the test distribution are unavailable during training. However, in many applications, a limited amount of test data may be available during training, yet properties of min-norm interpolation in this setting are not well-understood. We address this gap by characterizing the bias and variance of pooled min-$\ell_2$-norm interpolation under covariate and model shifts. The pooled interpolator captures both early fusion and a form of intermediate fusion. Our results have several implications: under model shift, for low signal-to-noise ratio (SNR), adding data always hurts. For higher SNR, transfer learning helps as long as the shift-to-signal (SSR) ratio lies below a threshold that we characterize explicitly. By consistently estimating these ratios, we provide a data-driven method to determine: (i) when the pooled interpolator outperforms the target-based interpolator, and (ii) the optimal number of target samples that minimizes the generalization error. Under covariate shift, if the source sample size is small relative to the dimension, heterogeneity between between domains improves the risk, and vice versa. We establish a novel anisotropic local law to achieve these characterizations, which may be of independent interest in random matrix theory. We supplement our theoretical characterizations with comprehensive simulations that demonstrate the finite-sample efficacy of our results.
ROTI-GCV: Generalized Cross-Validation for right-ROTationally Invariant Data
Jun 17, 2024Abstract:Two key tasks in high-dimensional regularized regression are tuning the regularization strength for good predictions and estimating the out-of-sample risk. It is known that the standard approach -- $k$-fold cross-validation -- is inconsistent in modern high-dimensional settings. While leave-one-out and generalized cross-validation remain consistent in some high-dimensional cases, they become inconsistent when samples are dependent or contain heavy-tailed covariates. To model structured sample dependence and heavy tails, we use right-rotationally invariant covariate distributions - a crucial concept from compressed sensing. In the common modern proportional asymptotics regime where the number of features and samples grow comparably, we introduce a new framework, ROTI-GCV, for reliably performing cross-validation. Along the way, we propose new estimators for the signal-to-noise ratio and noise variance under these challenging conditions. We conduct extensive experiments that demonstrate the power of our approach and its superiority over existing methods.
Predictive Inference in Multi-environment Scenarios
Mar 25, 2024Abstract:We address the challenge of constructing valid confidence intervals and sets in problems of prediction across multiple environments. We investigate two types of coverage suitable for these problems, extending the jackknife and split-conformal methods to show how to obtain distribution-free coverage in such non-traditional, hierarchical data-generating scenarios. Our contributions also include extensions for settings with non-real-valued responses and a theory of consistency for predictive inference in these general problems. We demonstrate a novel resizing method to adapt to problem difficulty, which applies both to existing approaches for predictive inference with hierarchical data and the methods we develop; this reduces prediction set sizes using limited information from the test environment, a key to the methods' practical performance, which we evaluate through neurochemical sensing and species classification datasets.
Spectrum-Aware Adjustment: A New Debiasing Framework with Applications to Principal Components Regression
Sep 14, 2023



Abstract:We introduce a new debiasing framework for high-dimensional linear regression that bypasses the restrictions on covariate distributions imposed by modern debiasing technology. We study the prevalent setting where the number of features and samples are both large and comparable. In this context, state-of-the-art debiasing technology uses a degrees-of-freedom correction to remove shrinkage bias of regularized estimators and conduct inference. However, this method requires that the observed samples are i.i.d., the covariates follow a mean zero Gaussian distribution, and reliable covariance matrix estimates for observed features are available. This approach struggles when (i) covariates are non-Gaussian with heavy tails or asymmetric distributions, (ii) rows of the design exhibit heterogeneity or dependencies, and (iii) reliable feature covariance estimates are lacking. To address these, we develop a new strategy where the debiasing correction is a rescaled gradient descent step (suitably initialized) with step size determined by the spectrum of the sample covariance matrix. Unlike prior work, we assume that eigenvectors of this matrix are uniform draws from the orthogonal group. We show this assumption remains valid in diverse situations where traditional debiasing fails, including designs with complex row-column dependencies, heavy tails, asymmetric properties, and latent low-rank structures. We establish asymptotic normality of our proposed estimator (centered and scaled) under various convergence notions. Moreover, we develop a consistent estimator for its asymptotic variance. Lastly, we introduce a debiased Principal Component Regression (PCR) technique using our Spectrum-Aware approach. In varied simulations and real data experiments, we observe that our method outperforms degrees-of-freedom debiasing by a margin.
Multi-Study Boosting: Theoretical Considerations for Merging vs. Ensembling
Jul 13, 2022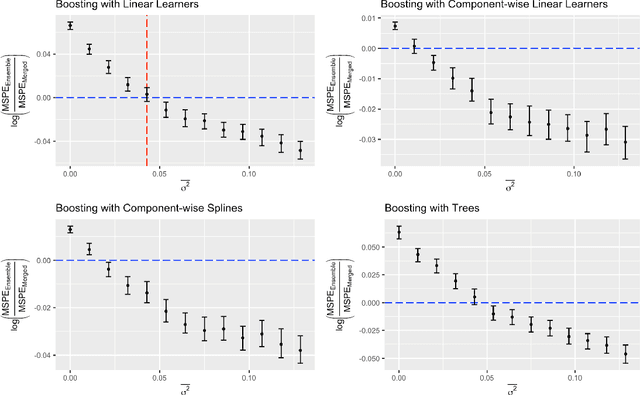
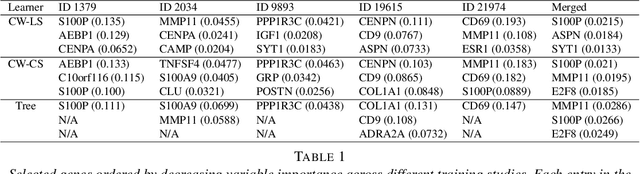
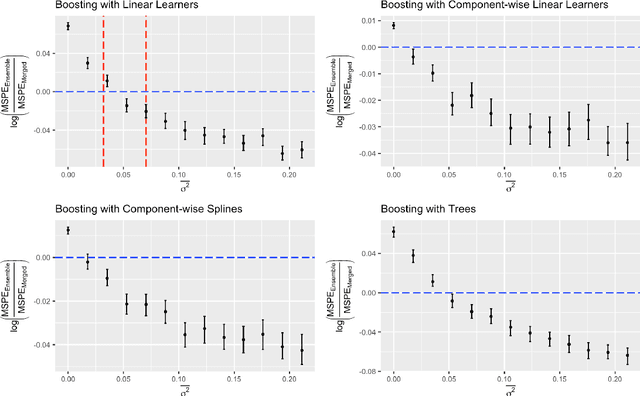
Abstract:Cross-study replicability is a powerful model evaluation criterion that emphasizes generalizability of predictions. When training cross-study replicable prediction models, it is critical to decide between merging and treating the studies separately. We study boosting algorithms in the presence of potential heterogeneity in predictor-outcome relationships across studies and compare two multi-study learning strategies: 1) merging all the studies and training a single model, and 2) multi-study ensembling, which involves training a separate model on each study and ensembling the resulting predictions. In the regression setting, we provide theoretical guidelines based on an analytical transition point to determine whether it is more beneficial to merge or to ensemble for boosting with linear learners. In addition, we characterize a bias-variance decomposition of estimation error for boosting with component-wise linear learners. We verify the theoretical transition point result in simulation and illustrate how it can guide the decision on merging vs. ensembling in an application to breast cancer gene expression data.
A New Central Limit Theorem for the Augmented IPW Estimator: Variance Inflation, Cross-Fit Covariance and Beyond
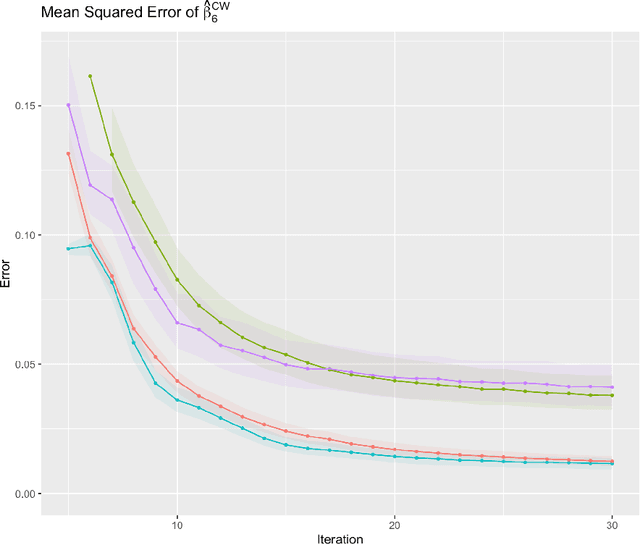
May 20, 2022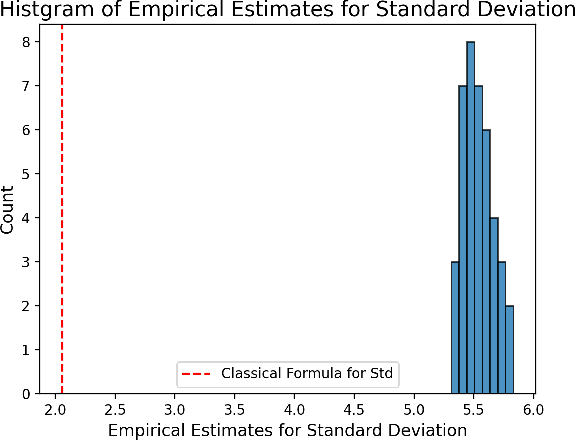
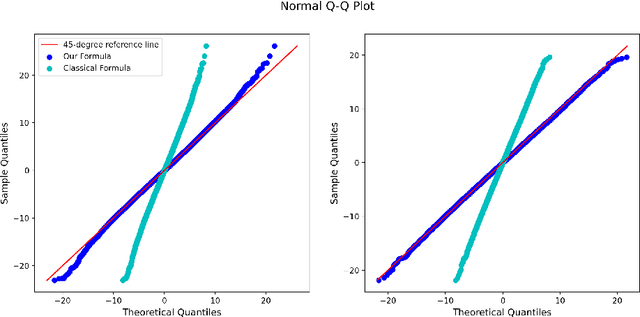
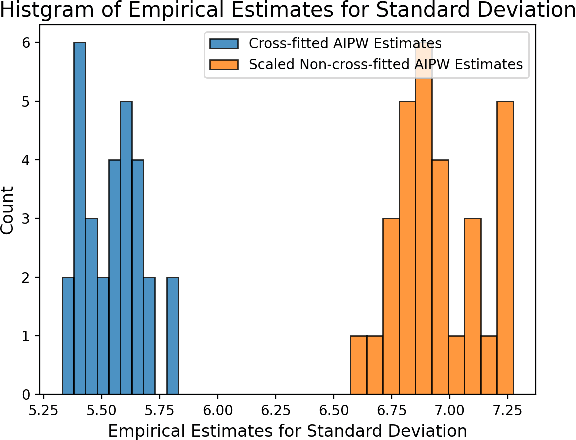
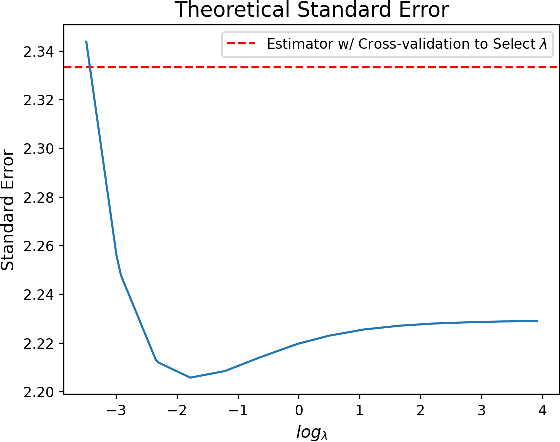
Abstract:Estimation of the average treatment effect (ATE) is a central problem in causal inference. In recent times, inference for the ATE in the presence of high-dimensional covariates has been extensively studied. Among the diverse approaches that have been proposed, augmented inverse probability weighting (AIPW) with cross-fitting has emerged as a popular choice in practice. In this work, we study this cross-fit AIPW estimator under well-specified outcome regression and propensity score models in a high-dimensional regime where the number of features and samples are both large and comparable. Under assumptions on the covariate distribution, we establish a new CLT for the suitably scaled cross-fit AIPW that applies without any sparsity assumptions on the underlying high-dimensional parameters. Our CLT uncovers two crucial phenomena among others: (i) the AIPW exhibits a substantial variance inflation that can be precisely quantified in terms of the signal-to-noise ratio and other problem parameters, (ii) the asymptotic covariance between the pre-cross-fit estimates is non-negligible even on the root-n scale. In fact, these cross-covariances turn out to be negative in our setting. These findings are strikingly different from their classical counterparts. On the technical front, our work utilizes a novel interplay between three distinct tools--approximate message passing theory, the theory of deterministic equivalents, and the leave-one-out approach. We believe our proof techniques should be useful for analyzing other two-stage estimators in this high-dimensional regime. Finally, we complement our theoretical results with simulations that demonstrate both the finite sample efficacy of our CLT and its robustness to our assumptions.
High-dimensional Asymptotics of Langevin Dynamics in Spiked Matrix Models
Apr 09, 2022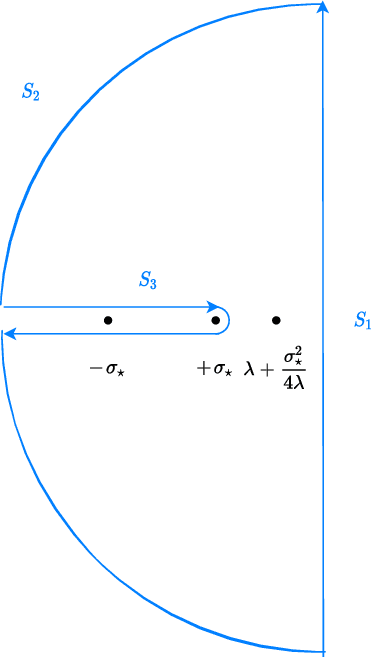
Abstract:We study Langevin dynamics for recovering the planted signal in the spiked matrix model. We provide a "path-wise" characterization of the overlap between the output of the Langevin algorithm and the planted signal. This overlap is characterized in terms of a self-consistent system of integro-differential equations, usually referred to as the Crisanti-Horner-Sommers-Cugliandolo-Kurchan (CHSCK) equations in the spin glass literature. As a second contribution, we derive an explicit formula for the limiting overlap in terms of the signal-to-noise ratio and the injected noise in the diffusion. This uncovers a sharp phase transition -- in one regime, the limiting overlap is strictly positive, while in the other, the injected noise overcomes the signal, and the limiting overlap is zero.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge