Understanding Optimal Feature Transfer via a Fine-Grained Bias-Variance Analysis

In the transfer learning paradigm models learn useful representations (or features) during a data-rich pretraining stage, and then use the pretrained representation to improve model performance on data-scarce downstream tasks. In this work, we explore transfer learning with the goal of optimizing downstream performance. We introduce a simple linear model that takes as input an arbitrary pretrained feature transform. We derive exact asymptotics of the downstream risk and its fine-grained bias-variance decomposition. Our finding suggests that using the ground-truth featurization can result in "double-divergence" of the asymptotic risk, indicating that it is not necessarily optimal for downstream performance. We then identify the optimal pretrained representation by minimizing the asymptotic downstream risk averaged over an ensemble of downstream tasks. Our analysis reveals the relative importance of learning the task-relevant features and structures in the data covariates and characterizes how each contributes to controlling the downstream risk from a bias-variance perspective. Moreover, we uncover a phase transition phenomenon where the optimal pretrained representation transitions from hard to soft selection of relevant features and discuss its connection to principal component regression.

Fundamental limits of community detection from multi-view data: multi-layer, dynamic and partially labeled block models

Multi-view data arises frequently in modern network analysis e.g. relations of multiple types among individuals in social network analysis, longitudinal measurements of interactions among observational units, annotated networks with noisy partial labeling of vertices etc. We study community detection in these disparate settings via a unified theoretical framework, and investigate the fundamental thresholds for community recovery. We characterize the mutual information between the data and the latent parameters, provided the degrees are sufficiently large. Based on this general result, (i) we derive a sharp threshold for community detection in an inhomogeneous multilayer block model \citep{chen2022global}, (ii) characterize a sharp threshold for weak recovery in a dynamic stochastic block model \citep{matias2017statistical}, and (iii) identify the limiting mutual information in an unbalanced partially labeled block model. Our first two results are derived modulo coordinate-wise convexity assumptions on specific functions -- we provide extensive numerical evidence for their correctness. Finally, we introduce iterative algorithms based on Approximate Message Passing for community detection in these problems.

A Mean Field Approach to Empirical Bayes Estimation in High-dimensional Linear Regression

We study empirical Bayes estimation in high-dimensional linear regression. To facilitate computationally efficient estimation of the underlying prior, we adopt a variational empirical Bayes approach, introduced originally in Carbonetto and Stephens (2012) and Kim et al. (2022). We establish asymptotic consistency of the nonparametric maximum likelihood estimator (NPMLE) and its (computable) naive mean field variational surrogate under mild assumptions on the design and the prior. Assuming, in addition, that the naive mean field approximation has a dominant optimizer, we develop a computationally efficient approximation to the oracle posterior distribution, and establish its accuracy under the 1-Wasserstein metric. This enables computationally feasible Bayesian inference; e.g., construction of posterior credible intervals with an average coverage guarantee, Bayes optimal estimation for the regression coefficients, estimation of the proportion of non-nulls, etc. Our analysis covers both deterministic and random designs, and accommodates correlations among the features. To the best of our knowledge, this provides the first rigorous nonparametric empirical Bayes method in a high-dimensional regression setting without sparsity.

Bayes optimal learning in high-dimensional linear regression with network side information

Supervised learning problems with side information in the form of a network arise frequently in applications in genomics, proteomics and neuroscience. For example, in genetic applications, the network side information can accurately capture background biological information on the intricate relations among the relevant genes. In this paper, we initiate a study of Bayes optimal learning in high-dimensional linear regression with network side information. To this end, we first introduce a simple generative model (called the Reg-Graph model) which posits a joint distribution for the supervised data and the observed network through a common set of latent parameters. Next, we introduce an iterative algorithm based on Approximate Message Passing (AMP) which is provably Bayes optimal under very general conditions. In addition, we characterize the limiting mutual information between the latent signal and the data observed, and thus precisely quantify the statistical impact of the network side information. Finally, supporting numerical experiments suggest that the introduced algorithm has excellent performance in finite samples.

Sparse Signal Detection in Heteroscedastic Gaussian Sequence Models: Sharp Minimax Rates

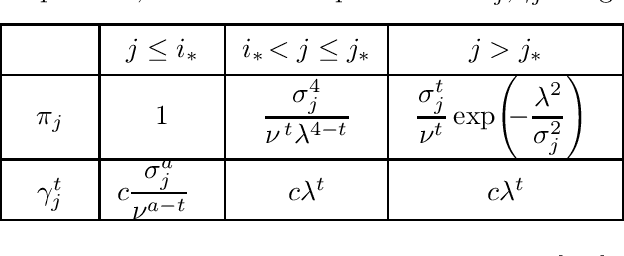
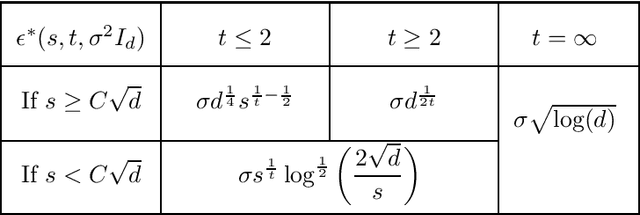
Given a heterogeneous Gaussian sequence model with unknown mean $\theta \in \mathbb R^d$ and known covariance matrix $\Sigma = \operatorname{diag}(\sigma_1^2,\dots, \sigma_d^2)$, we study the signal detection problem against sparse alternatives, for known sparsity $s$. Namely, we characterize how large $\epsilon^*>0$ should be, in order to distinguish with high probability the null hypothesis $\theta=0$ from the alternative composed of $s$-sparse vectors in $\mathbb R^d$, separated from $0$ in $L^t$ norm ($t \geq 1$) by at least $\epsilon^*$. We find minimax upper and lower bounds over the minimax separation radius $\epsilon^*$ and prove that they are always matching. We also derive the corresponding minimax tests achieving these bounds. Our results reveal new phase transitions regarding the behavior of $\epsilon^*$ with respect to the level of sparsity, to the $L^t$ metric, and to the heteroscedasticity profile of $\Sigma$. In the case of the Euclidean (i.e. $L^2$) separation, we bridge the remaining gaps in the literature.

A New Central Limit Theorem for the Augmented IPW Estimator: Variance Inflation, Cross-Fit Covariance and Beyond

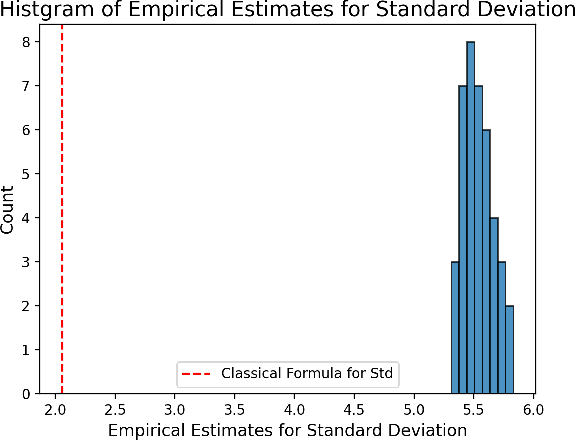
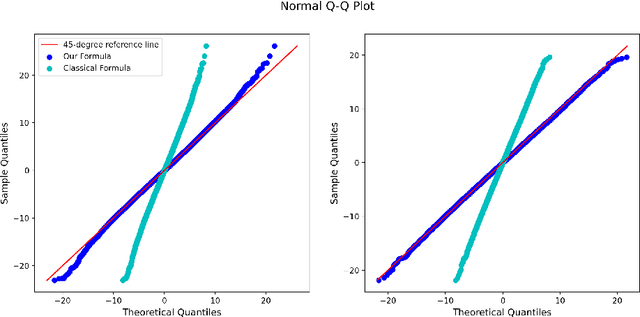
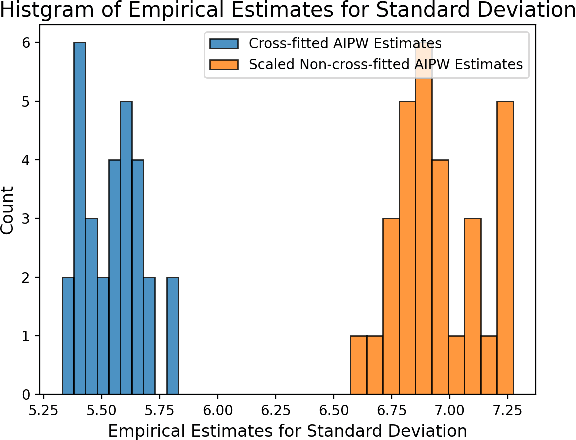
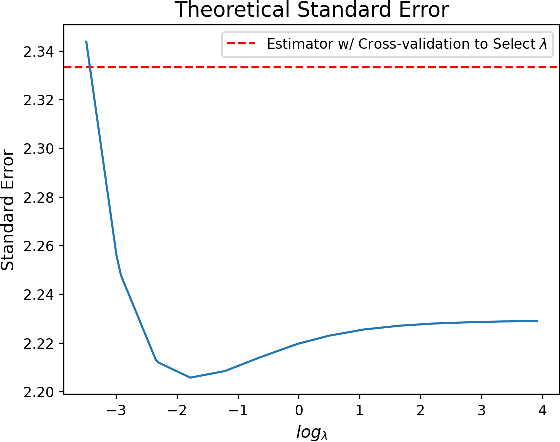
Estimation of the average treatment effect (ATE) is a central problem in causal inference. In recent times, inference for the ATE in the presence of high-dimensional covariates has been extensively studied. Among the diverse approaches that have been proposed, augmented inverse probability weighting (AIPW) with cross-fitting has emerged as a popular choice in practice. In this work, we study this cross-fit AIPW estimator under well-specified outcome regression and propensity score models in a high-dimensional regime where the number of features and samples are both large and comparable. Under assumptions on the covariate distribution, we establish a new CLT for the suitably scaled cross-fit AIPW that applies without any sparsity assumptions on the underlying high-dimensional parameters. Our CLT uncovers two crucial phenomena among others: (i) the AIPW exhibits a substantial variance inflation that can be precisely quantified in terms of the signal-to-noise ratio and other problem parameters, (ii) the asymptotic covariance between the pre-cross-fit estimates is non-negligible even on the root-n scale. In fact, these cross-covariances turn out to be negative in our setting. These findings are strikingly different from their classical counterparts. On the technical front, our work utilizes a novel interplay between three distinct tools--approximate message passing theory, the theory of deterministic equivalents, and the leave-one-out approach. We believe our proof techniques should be useful for analyzing other two-stage estimators in this high-dimensional regime. Finally, we complement our theoretical results with simulations that demonstrate both the finite sample efficacy of our CLT and its robustness to our assumptions.

High-dimensional Asymptotics of Langevin Dynamics in Spiked Matrix Models

We study Langevin dynamics for recovering the planted signal in the spiked matrix model. We provide a "path-wise" characterization of the overlap between the output of the Langevin algorithm and the planted signal. This overlap is characterized in terms of a self-consistent system of integro-differential equations, usually referred to as the Crisanti-Horner-Sommers-Cugliandolo-Kurchan (CHSCK) equations in the spin glass literature. As a second contribution, we derive an explicit formula for the limiting overlap in terms of the signal-to-noise ratio and the injected noise in the diffusion. This uncovers a sharp phase transition -- in one regime, the limiting overlap is strictly positive, while in the other, the injected noise overcomes the signal, and the limiting overlap is zero.

The TAP free energy for high-dimensional linear regression

We derive a variational representation for the log-normalizing constant of the posterior distribution in Bayesian linear regression with a uniform spherical prior and an i.i.d. Gaussian design. We work under the "proportional" asymptotic regime, where the number of observations and the number of features grow at a proportional rate. This rigorously establishes the Thouless-Anderson-Palmer (TAP) approximation arising from spin glass theory, and proves a conjecture of Krzakala et. al. (2014) in the special case of the spherical prior.

Variational Inference in high-dimensional linear regression

We study high-dimensional Bayesian linear regression with product priors. Using the nascent theory of non-linear large deviations (Chatterjee and Dembo,2016), we derive sufficient conditions for the leading-order correctness of the naive mean-field approximation to the log-normalizing constant of the posterior distribution. Subsequently, assuming a true linear model for the observed data, we derive a limiting infinite dimensional variational formula for the log normalizing constant of the posterior. Furthermore, we establish that under an additional "separation" condition, the variational problem has a unique optimizer, and this optimizer governs the probabilistic properties of the posterior distribution. We provide intuitive sufficient conditions for the validity of this "separation" condition. Finally, we illustrate our results on concrete examples with specific design matrices.