Clustering by Denoising: Latent plug-and-play diffusion for single-cell data

Single-cell RNA sequencing (scRNA-seq) enables the study of cellular heterogeneity. Yet, clustering accuracy, and with it downstream analyses based on cell labels, remain challenging due to measurement noise and biological variability. In standard latent spaces (e.g., obtained through PCA), data from different cell types can be projected close together, making accurate clustering difficult. We introduce a latent plug-and-play diffusion framework that separates the observation and denoising space. This separation is operationalized through a novel Gibbs sampling procedure: the learned diffusion prior is applied in a low-dimensional latent space to perform denoising, while to steer this process, noise is reintroduced into the original high-dimensional observation space. This unique "input-space steering" ensures the denoising trajectory remains faithful to the original data structure. Our approach offers three key advantages: (1) adaptive noise handling via a tunable balance between prior and observed data; (2) uncertainty quantification through principled uncertainty estimates for downstream analysis; and (3) generalizable denoising by leveraging clean reference data to denoise noisier datasets, and via averaging, improve quality beyond the training set. We evaluate robustness on both synthetic and real single-cell genomics data. Our method improves clustering accuracy on synthetic data across varied noise levels and dataset shifts. On real-world single-cell data, our method demonstrates improved biological coherence in the resulting cell clusters, with cluster boundaries that better align with known cell type markers and developmental trajectories.

How Private is Your Attention? Bridging Privacy with In-Context Learning

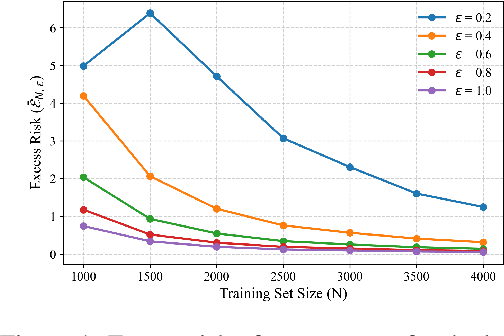
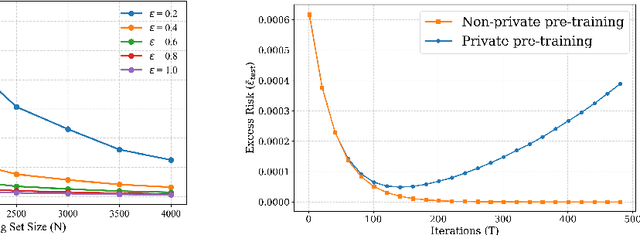
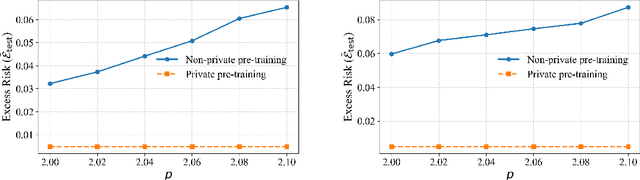
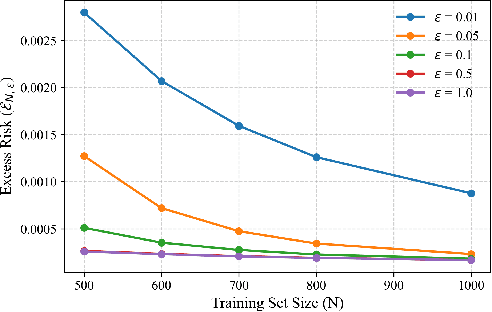
In-context learning (ICL)-the ability of transformer-based models to perform new tasks from examples provided at inference time-has emerged as a hallmark of modern language models. While recent works have investigated the mechanisms underlying ICL, its feasibility under formal privacy constraints remains largely unexplored. In this paper, we propose a differentially private pretraining algorithm for linear attention heads and present the first theoretical analysis of the privacy-accuracy trade-off for ICL in linear regression. Our results characterize the fundamental tension between optimization and privacy-induced noise, formally capturing behaviors observed in private training via iterative methods. Additionally, we show that our method is robust to adversarial perturbations of training prompts, unlike standard ridge regression. All theoretical findings are supported by extensive simulations across diverse settings.

Degree Heterogeneity in Higher-Order Networks: Inference in the Hypergraph $\boldsymbolβ$-Model

The $\boldsymbol{\beta}$-model for random graphs is commonly used for representing pairwise interactions in a network with degree heterogeneity. Going beyond pairwise interactions, Stasi et al. (2014) introduced the hypergraph $\boldsymbol{\beta}$-model for capturing degree heterogeneity in networks with higher-order (multi-way) interactions. In this paper we initiate the rigorous study of the hypergraph $\boldsymbol{\beta}$-model with multiple layers, which allows for hyperedges of different sizes across the layers. To begin with, we derive the rates of convergence of the maximum likelihood (ML) estimate and establish their minimax rate optimality. We also derive the limiting distribution of the ML estimate and construct asymptotically valid confidence intervals for the model parameters. Next, we consider the goodness-of-fit problem in the hypergraph $\boldsymbol{\beta}$-model. Specifically, we establish the asymptotic normality of the likelihood ratio (LR) test under the null hypothesis, derive its detection threshold, and also its limiting power at the threshold. Interestingly, the detection threshold of the LR test turns out to be minimax optimal, that is, all tests are asymptotically powerless below this threshold. The theoretical results are further validated in numerical experiments. In addition to developing the theoretical framework for estimation and inference for hypergraph $\boldsymbol{\beta}$-models, the above results fill a number of gaps in the graph $\boldsymbol{\beta}$-model literature, such as the minimax optimality of the ML estimates and the non-null properties of the LR test, which, to the best of our knowledge, have not been studied before.

Bayes optimal learning in high-dimensional linear regression with network side information

Supervised learning problems with side information in the form of a network arise frequently in applications in genomics, proteomics and neuroscience. For example, in genetic applications, the network side information can accurately capture background biological information on the intricate relations among the relevant genes. In this paper, we initiate a study of Bayes optimal learning in high-dimensional linear regression with network side information. To this end, we first introduce a simple generative model (called the Reg-Graph model) which posits a joint distribution for the supervised data and the observed network through a common set of latent parameters. Next, we introduce an iterative algorithm based on Approximate Message Passing (AMP) which is provably Bayes optimal under very general conditions. In addition, we characterize the limiting mutual information between the latent signal and the data observed, and thus precisely quantify the statistical impact of the network side information. Finally, supporting numerical experiments suggest that the introduced algorithm has excellent performance in finite samples.