How Private is Your Attention? Bridging Privacy with In-Context Learning

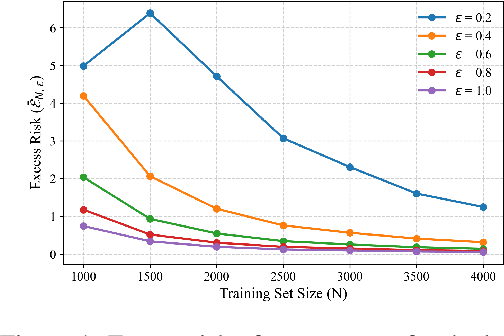
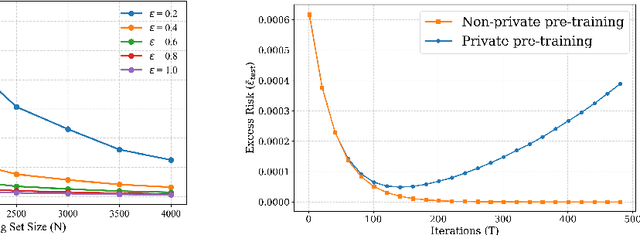
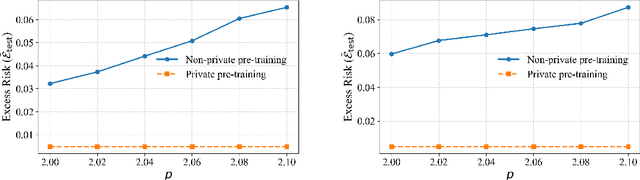
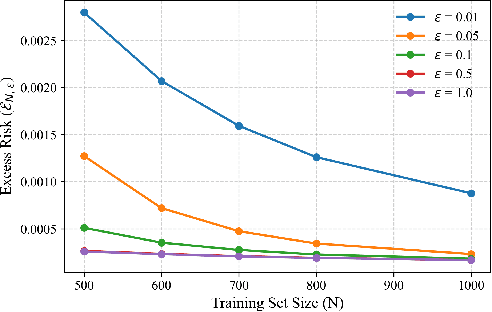
In-context learning (ICL)-the ability of transformer-based models to perform new tasks from examples provided at inference time-has emerged as a hallmark of modern language models. While recent works have investigated the mechanisms underlying ICL, its feasibility under formal privacy constraints remains largely unexplored. In this paper, we propose a differentially private pretraining algorithm for linear attention heads and present the first theoretical analysis of the privacy-accuracy trade-off for ICL in linear regression. Our results characterize the fundamental tension between optimization and privacy-induced noise, formally capturing behaviors observed in private training via iterative methods. Additionally, we show that our method is robust to adversarial perturbations of training prompts, unlike standard ridge regression. All theoretical findings are supported by extensive simulations across diverse settings.

Riemannian Residual Neural Networks

Recent methods in geometric deep learning have introduced various neural networks to operate over data that lie on Riemannian manifolds. Such networks are often necessary to learn well over graphs with a hierarchical structure or to learn over manifold-valued data encountered in the natural sciences. These networks are often inspired by and directly generalize standard Euclidean neural networks. However, extending Euclidean networks is difficult and has only been done for a select few manifolds. In this work, we examine the residual neural network (ResNet) and show how to extend this construction to general Riemannian manifolds in a geometrically principled manner. Originally introduced to help solve the vanishing gradient problem, ResNets have become ubiquitous in machine learning due to their beneficial learning properties, excellent empirical results, and easy-to-incorporate nature when building varied neural networks. We find that our Riemannian ResNets mirror these desirable properties: when compared to existing manifold neural networks designed to learn over hyperbolic space and the manifold of symmetric positive definite matrices, we outperform both kinds of networks in terms of relevant testing metrics and training dynamics.

Model-assisted deep learning of rare extreme events from partial observations

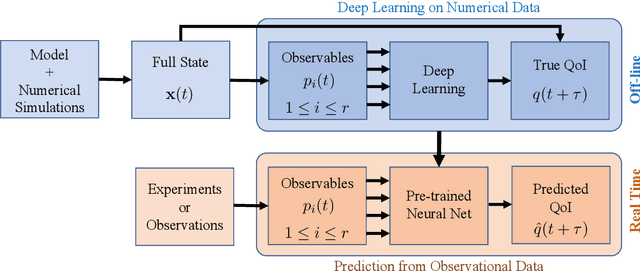
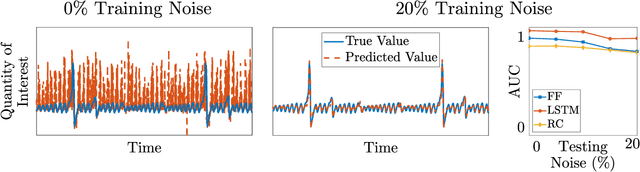
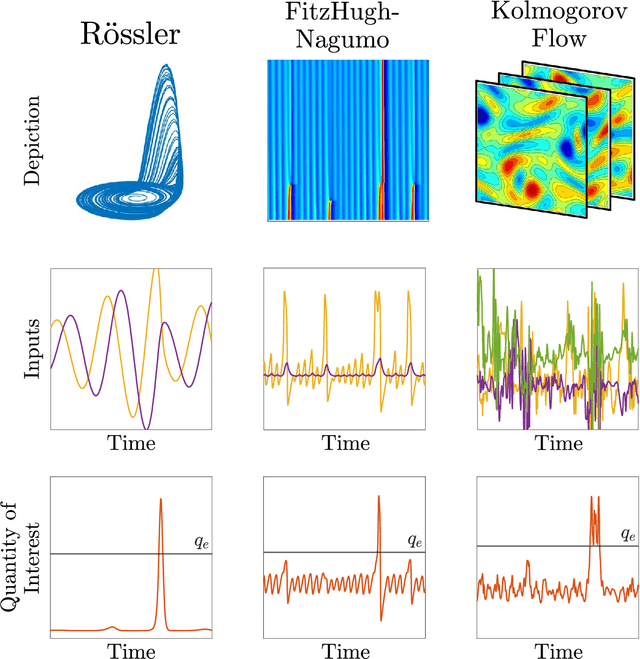
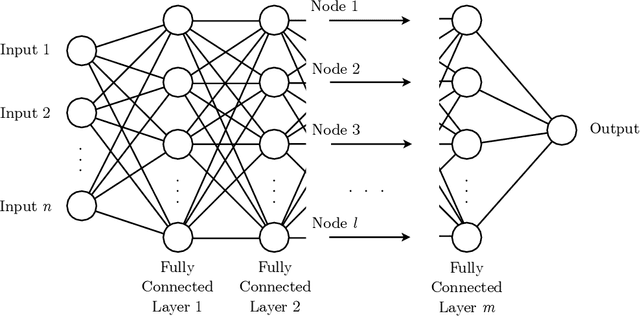
To predict rare extreme events using deep neural networks, one encounters the so-called small data problem because even long-term observations often contain few extreme events. Here, we investigate a model-assisted framework where the training data is obtained from numerical simulations, as opposed to observations, with adequate samples from extreme events. However, to ensure the trained networks are applicable in practice, the training is not performed on the full simulation data; instead we only use a small subset of observable quantities which can be measured in practice. We investigate the feasibility of this model-assisted framework on three different dynamical systems (Rossler attractor, FitzHugh--Nagumo model, and a turbulent fluid flow) and three different deep neural network architectures (feedforward, long short-term memory, and reservoir computing). In each case, we study the prediction accuracy, robustness to noise, reproducibility under repeated training, and sensitivity to the type of input data. In particular, we find long short-term memory networks to be most robust to noise and to yield relatively accurate predictions, while requiring minimal fine-tuning of the hyperparameters.