Geometric Trajectory Diffusion Models

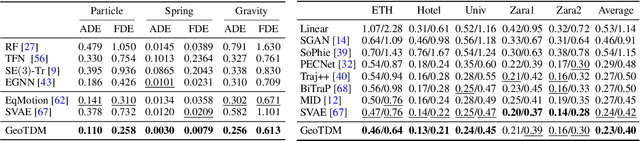
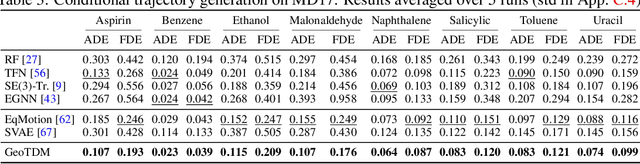
Generative models have shown great promise in generating 3D geometric systems, which is a fundamental problem in many natural science domains such as molecule and protein design. However, existing approaches only operate on static structures, neglecting the fact that physical systems are always dynamic in nature. In this work, we propose geometric trajectory diffusion models (GeoTDM), the first diffusion model for modeling the temporal distribution of 3D geometric trajectories. Modeling such distribution is challenging as it requires capturing both the complex spatial interactions with physical symmetries and temporal correspondence encapsulated in the dynamics. We theoretically justify that diffusion models with equivariant temporal kernels can lead to density with desired symmetry, and develop a novel transition kernel leveraging SE(3)-equivariant spatial convolution and temporal attention. Furthermore, to induce an expressive trajectory distribution for conditional generation, we introduce a generalized learnable geometric prior into the forward diffusion process to enhance temporal conditioning. We conduct extensive experiments on both unconditional and conditional generation in various scenarios, including physical simulation, molecular dynamics, and pedestrian motion. Empirical results on a wide suite of metrics demonstrate that GeoTDM can generate realistic geometric trajectories with significantly higher quality.

Equivariant Graph Neural Operator for Modeling 3D Dynamics

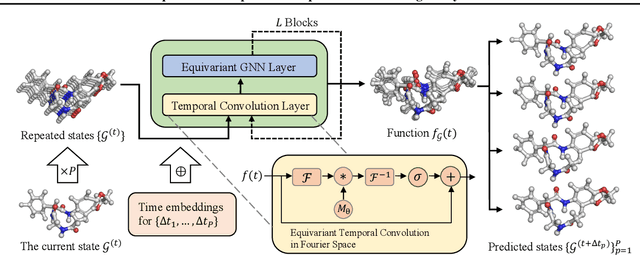
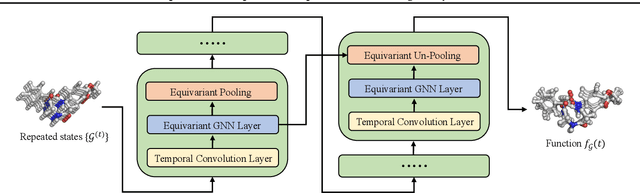
Modeling the complex three-dimensional (3D) dynamics of relational systems is an important problem in the natural sciences, with applications ranging from molecular simulations to particle mechanics. Machine learning methods have achieved good success by learning graph neural networks to model spatial interactions. However, these approaches do not faithfully capture temporal correlations since they only model next-step predictions. In this work, we propose Equivariant Graph Neural Operator (EGNO), a novel and principled method that directly models dynamics as trajectories instead of just next-step prediction. Different from existing methods, EGNO explicitly learns the temporal evolution of 3D dynamics where we formulate the dynamics as a function over time and learn neural operators to approximate it. To capture the temporal correlations while keeping the intrinsic SE(3)-equivariance, we develop equivariant temporal convolutions parameterized in the Fourier space and build EGNO by stacking the Fourier layers over equivariant networks. EGNO is the first operator learning framework that is capable of modeling solution dynamics functions over time while retaining 3D equivariance. Comprehensive experiments in multiple domains, including particle simulations, human motion capture, and molecular dynamics, demonstrate the significantly superior performance of EGNO against existing methods, thanks to the equivariant temporal modeling.

Diffusion Model Alignment Using Direct Preference Optimization

Large language models (LLMs) are fine-tuned using human comparison data with Reinforcement Learning from Human Feedback (RLHF) methods to make them better aligned with users' preferences. In contrast to LLMs, human preference learning has not been widely explored in text-to-image diffusion models; the best existing approach is to fine-tune a pretrained model using carefully curated high quality images and captions to improve visual appeal and text alignment. We propose Diffusion-DPO, a method to align diffusion models to human preferences by directly optimizing on human comparison data. Diffusion-DPO is adapted from the recently developed Direct Preference Optimization (DPO), a simpler alternative to RLHF which directly optimizes a policy that best satisfies human preferences under a classification objective. We re-formulate DPO to account for a diffusion model notion of likelihood, utilizing the evidence lower bound to derive a differentiable objective. Using the Pick-a-Pic dataset of 851K crowdsourced pairwise preferences, we fine-tune the base model of the state-of-the-art Stable Diffusion XL (SDXL)-1.0 model with Diffusion-DPO. Our fine-tuned base model significantly outperforms both base SDXL-1.0 and the larger SDXL-1.0 model consisting of an additional refinement model in human evaluation, improving visual appeal and prompt alignment. We also develop a variant that uses AI feedback and has comparable performance to training on human preferences, opening the door for scaling of diffusion model alignment methods.

Scaling Riemannian Diffusion Models

Riemannian diffusion models draw inspiration from standard Euclidean space diffusion models to learn distributions on general manifolds. Unfortunately, the additional geometric complexity renders the diffusion transition term inexpressible in closed form, so prior methods resort to imprecise approximations of the score matching training objective that degrade performance and preclude applications in high dimensions. In this work, we reexamine these approximations and propose several practical improvements. Our key observation is that most relevant manifolds are symmetric spaces, which are much more amenable to computation. By leveraging and combining various ans\"{a}tze, we can quickly compute relevant quantities to high precision. On low dimensional datasets, our correction produces a noticeable improvement, allowing diffusion to compete with other methods. Additionally, we show that our method enables us to scale to high dimensional tasks on nontrivial manifolds. In particular, we model QCD densities on $SU(n)$ lattices and contrastively learned embeddings on high dimensional hyperspheres.

Discrete Diffusion Language Modeling by Estimating the Ratios of the Data Distribution

Despite their groundbreaking performance for many generative modeling tasks, diffusion models have fallen short on discrete data domains such as natural language. Crucially, standard diffusion models rely on the well-established theory of score matching, but efforts to generalize this to discrete structures have not yielded the same empirical gains. In this work, we bridge this gap by proposing score entropy, a novel discrete score matching loss that is more stable than existing methods, forms an ELBO for maximum likelihood training, and can be efficiently optimized with a denoising variant. We scale our Score Entropy Discrete Diffusion models (SEDD) to the experimental setting of GPT-2, achieving highly competitive likelihoods while also introducing distinct algorithmic advantages. In particular, when comparing similarly sized SEDD and GPT-2 models, SEDD attains comparable perplexities (normally within $+10\%$ of and sometimes outperforming the baseline). Furthermore, SEDD models learn a more faithful sequence distribution (around $4\times$ better compared to GPT-2 models with ancestral sampling as measured by large models), can trade off compute for generation quality (needing only $16\times$ fewer network evaluations to match GPT-2), and enables arbitrary infilling beyond the standard left to right prompting.

Riemannian Residual Neural Networks

Recent methods in geometric deep learning have introduced various neural networks to operate over data that lie on Riemannian manifolds. Such networks are often necessary to learn well over graphs with a hierarchical structure or to learn over manifold-valued data encountered in the natural sciences. These networks are often inspired by and directly generalize standard Euclidean neural networks. However, extending Euclidean networks is difficult and has only been done for a select few manifolds. In this work, we examine the residual neural network (ResNet) and show how to extend this construction to general Riemannian manifolds in a geometrically principled manner. Originally introduced to help solve the vanishing gradient problem, ResNets have become ubiquitous in machine learning due to their beneficial learning properties, excellent empirical results, and easy-to-incorporate nature when building varied neural networks. We find that our Riemannian ResNets mirror these desirable properties: when compared to existing manifold neural networks designed to learn over hyperbolic space and the manifold of symmetric positive definite matrices, we outperform both kinds of networks in terms of relevant testing metrics and training dynamics.

Denoising Diffusion Bridge Models

Diffusion models are powerful generative models that map noise to data using stochastic processes. However, for many applications such as image editing, the model input comes from a distribution that is not random noise. As such, diffusion models must rely on cumbersome methods like guidance or projected sampling to incorporate this information in the generative process. In our work, we propose Denoising Diffusion Bridge Models (DDBMs), a natural alternative to this paradigm based on diffusion bridges, a family of processes that interpolate between two paired distributions given as endpoints. Our method learns the score of the diffusion bridge from data and maps from one endpoint distribution to the other by solving a (stochastic) differential equation based on the learned score. Our method naturally unifies several classes of generative models, such as score-based diffusion models and OT-Flow-Matching, allowing us to adapt existing design and architectural choices to our more general problem. Empirically, we apply DDBMs to challenging image datasets in both pixel and latent space. On standard image translation problems, DDBMs achieve significant improvement over baseline methods, and, when we reduce the problem to image generation by setting the source distribution to random noise, DDBMs achieve comparable FID scores to state-of-the-art methods despite being built for a more general task.

Reflected Diffusion Models

Score-based diffusion models learn to reverse a stochastic differential equation that maps data to noise. However, for complex tasks, numerical error can compound and result in highly unnatural samples. Previous work mitigates this drift with thresholding, which projects to the natural data domain (such as pixel space for images) after each diffusion step, but this leads to a mismatch between the training and generative processes. To incorporate data constraints in a principled manner, we present Reflected Diffusion Models, which instead reverse a reflected stochastic differential equation evolving on the support of the data. Our approach learns the perturbed score function through a generalized score matching loss and extends key components of standard diffusion models including diffusion guidance, likelihood-based training, and ODE sampling. We also bridge the theoretical gap with thresholding: such schemes are just discretizations of reflected SDEs. On standard image benchmarks, our method is competitive with or surpasses the state of the art and, for classifier-free guidance, our approach enables fast exact sampling with ODEs and produces more faithful samples under high guidance weight.

Intrinsic Dimension, Persistent Homology and Generalization in Neural Networks

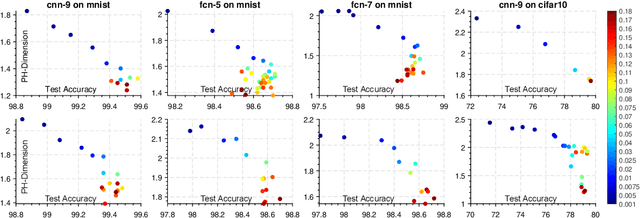
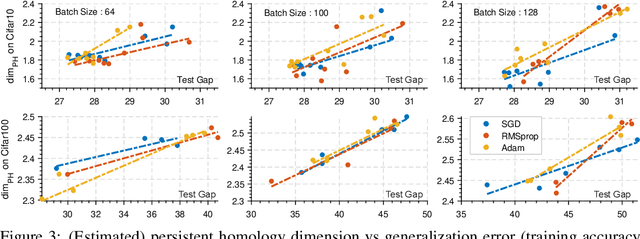
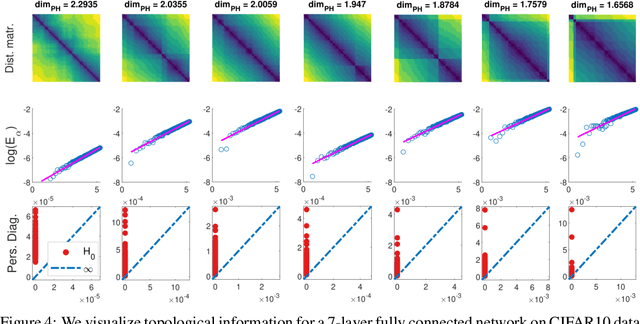
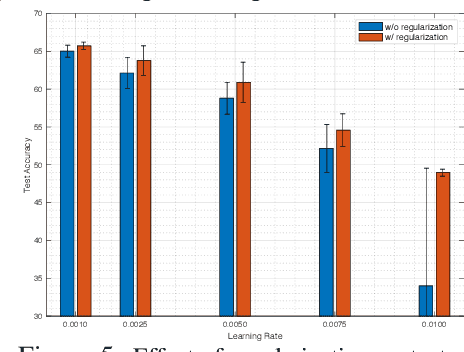
Disobeying the classical wisdom of statistical learning theory, modern deep neural networks generalize well even though they typically contain millions of parameters. Recently, it has been shown that the trajectories of iterative optimization algorithms can possess fractal structures, and their generalization error can be formally linked to the complexity of such fractals. This complexity is measured by the fractal's intrinsic dimension, a quantity usually much smaller than the number of parameters in the network. Even though this perspective provides an explanation for why overparametrized networks would not overfit, computing the intrinsic dimension (e.g., for monitoring generalization during training) is a notoriously difficult task, where existing methods typically fail even in moderate ambient dimensions. In this study, we consider this problem from the lens of topological data analysis (TDA) and develop a generic computational tool that is built on rigorous mathematical foundations. By making a novel connection between learning theory and TDA, we first illustrate that the generalization error can be equivalently bounded in terms of a notion called the 'persistent homology dimension' (PHD), where, compared with prior work, our approach does not require any additional geometrical or statistical assumptions on the training dynamics. Then, by utilizing recently established theoretical results and TDA tools, we develop an efficient algorithm to estimate PHD in the scale of modern deep neural networks and further provide visualization tools to help understand generalization in deep learning. Our experiments show that the proposed approach can efficiently compute a network's intrinsic dimension in a variety of settings, which is predictive of the generalization error.

Equivariant Manifold Flows

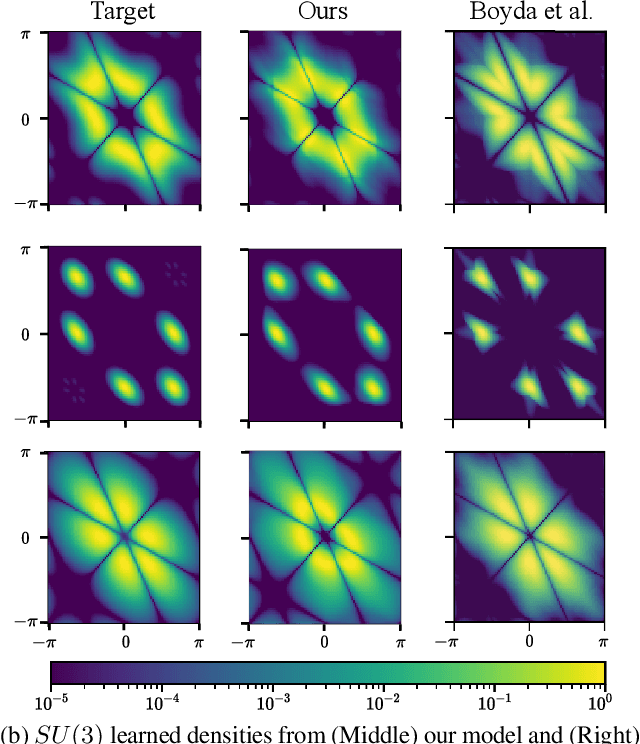
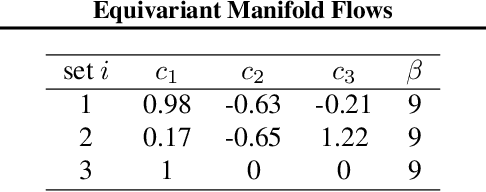
Tractably modelling distributions over manifolds has long been an important goal in the natural sciences. Recent work has focused on developing general machine learning models to learn such distributions. However, for many applications these distributions must respect manifold symmetries -- a trait which most previous models disregard. In this paper, we lay the theoretical foundations for learning symmetry-invariant distributions on arbitrary manifolds via equivariant manifold flows. We demonstrate the utility of our approach by using it to learn gauge invariant densities over $SU(n)$ in the context of quantum field theory.