Revisiting the Necessity of Graph Learning and Common Graph Benchmarks

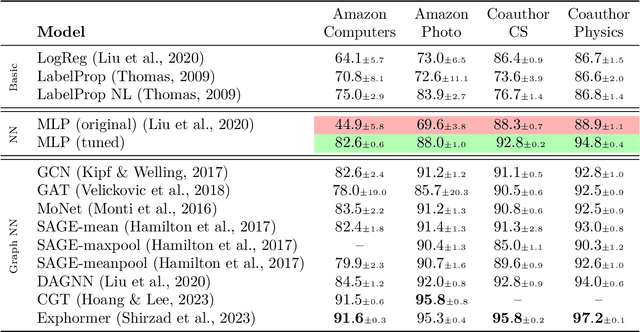
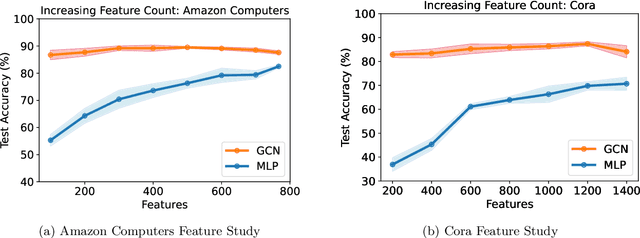
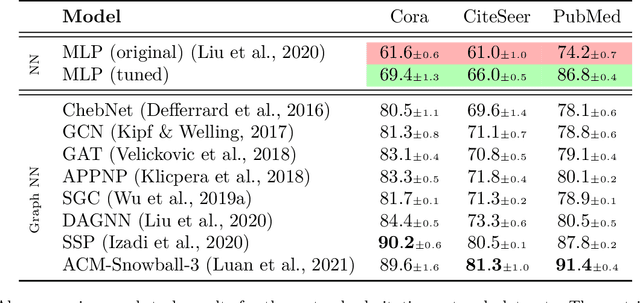
Graph machine learning has enjoyed a meteoric rise in popularity since the introduction of deep learning in graph contexts. This is no surprise due to the ubiquity of graph data in large scale industrial settings. Tacitly assumed in all graph learning tasks is the separation of the graph structure and node features: node features strictly encode individual data while the graph structure consists only of pairwise interactions. The driving belief is that node features are (by themselves) insufficient for these tasks, so benchmark performance accurately reflects improvements in graph learning. In our paper, we challenge this orthodoxy by showing that, surprisingly, node features are oftentimes more-than-sufficient for many common graph benchmarks, breaking this critical assumption. When comparing against a well-tuned feature-only MLP baseline on seven of the most commonly used graph learning datasets, one gains little benefit from using graph structure on five datasets. We posit that these datasets do not benefit considerably from graph learning because the features themselves already contain enough graph information to obviate or substantially reduce the need for the graph. To illustrate this point, we perform a feature study on these datasets and show how the features are responsible for closing the gap between MLP and graph-method performance. Further, in service of introducing better empirical measures of progress for graph neural networks, we present a challenging parametric family of principled synthetic datasets that necessitate graph information for nontrivial performance. Lastly, we section out a subset of real-world datasets that are not trivially solved by an MLP and hence serve as reasonable benchmarks for graph neural networks.

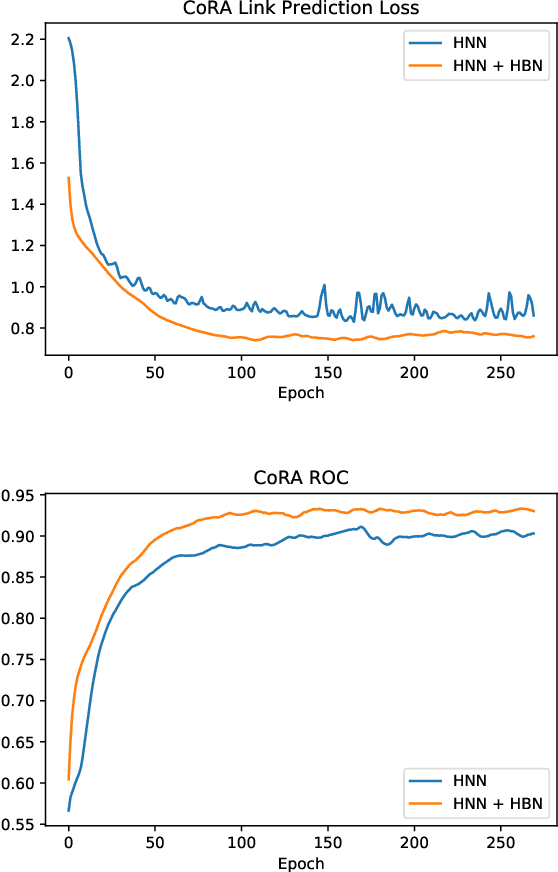
Shedding Light on Problems with Hyperbolic Graph Learning

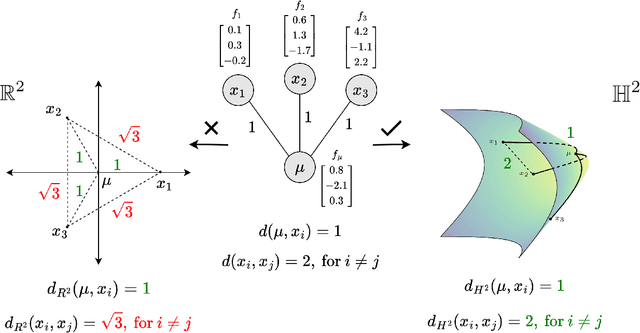
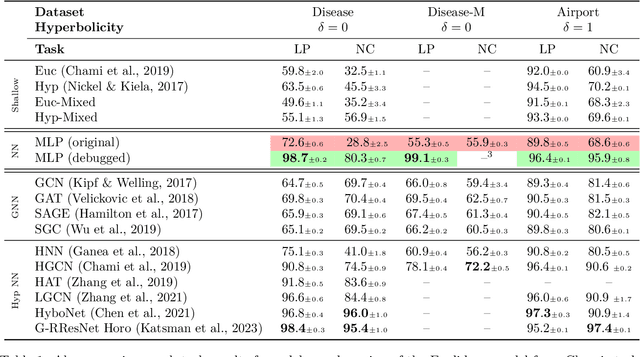
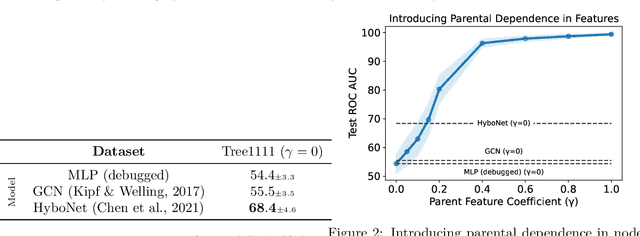
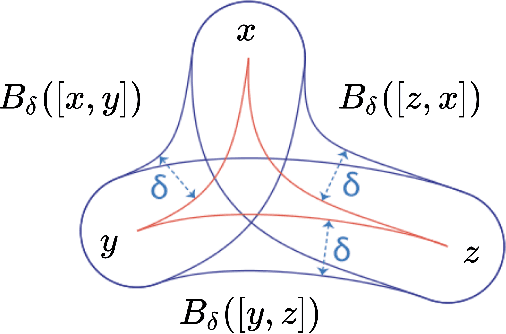
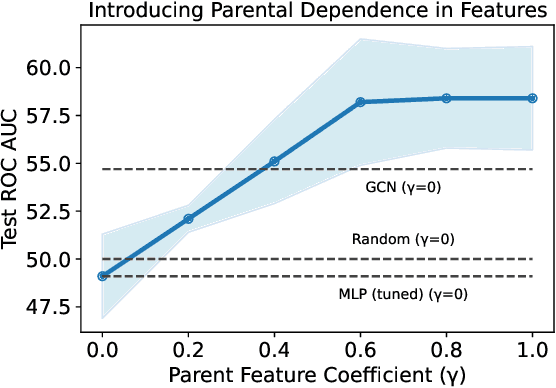
Recent papers in the graph machine learning literature have introduced a number of approaches for hyperbolic representation learning. The asserted benefits are improved performance on a variety of graph tasks, node classification and link prediction included. Claims have also been made about the geometric suitability of particular hierarchical graph datasets to representation in hyperbolic space. Despite these claims, our work makes a surprising discovery: when simple Euclidean models with comparable numbers of parameters are properly trained in the same environment, in most cases, they perform as well, if not better, than all introduced hyperbolic graph representation learning models, even on graph datasets previously claimed to be the most hyperbolic as measured by Gromov $\delta$-hyperbolicity (i.e., perfect trees). This observation gives rise to a simple question: how can this be? We answer this question by taking a careful look at the field of hyperbolic graph representation learning as it stands today, and find that a number of papers fail to diligently present baselines, make faulty modelling assumptions when constructing algorithms, and use misleading metrics to quantify geometry of graph datasets. We take a closer look at each of these three problems, elucidate the issues, perform an analysis of methods, and introduce a parametric family of benchmark datasets to ascertain the applicability of (hyperbolic) graph neural networks.

Riemannian Residual Neural Networks

Recent methods in geometric deep learning have introduced various neural networks to operate over data that lie on Riemannian manifolds. Such networks are often necessary to learn well over graphs with a hierarchical structure or to learn over manifold-valued data encountered in the natural sciences. These networks are often inspired by and directly generalize standard Euclidean neural networks. However, extending Euclidean networks is difficult and has only been done for a select few manifolds. In this work, we examine the residual neural network (ResNet) and show how to extend this construction to general Riemannian manifolds in a geometrically principled manner. Originally introduced to help solve the vanishing gradient problem, ResNets have become ubiquitous in machine learning due to their beneficial learning properties, excellent empirical results, and easy-to-incorporate nature when building varied neural networks. We find that our Riemannian ResNets mirror these desirable properties: when compared to existing manifold neural networks designed to learn over hyperbolic space and the manifold of symmetric positive definite matrices, we outperform both kinds of networks in terms of relevant testing metrics and training dynamics.

Equivariant Manifold Flows

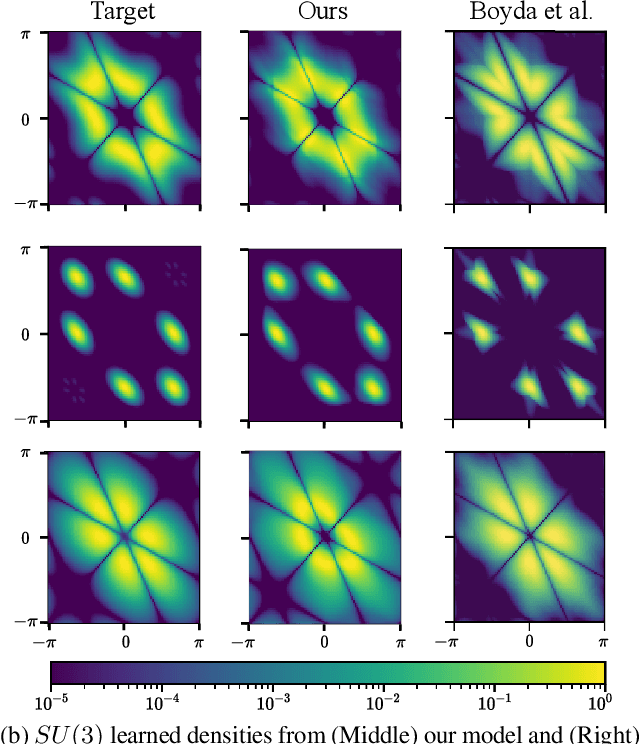
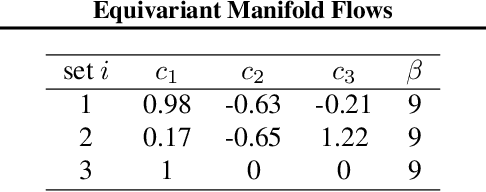
Tractably modelling distributions over manifolds has long been an important goal in the natural sciences. Recent work has focused on developing general machine learning models to learn such distributions. However, for many applications these distributions must respect manifold symmetries -- a trait which most previous models disregard. In this paper, we lay the theoretical foundations for learning symmetry-invariant distributions on arbitrary manifolds via equivariant manifold flows. We demonstrate the utility of our approach by using it to learn gauge invariant densities over $SU(n)$ in the context of quantum field theory.

Neural Manifold Ordinary Differential Equations

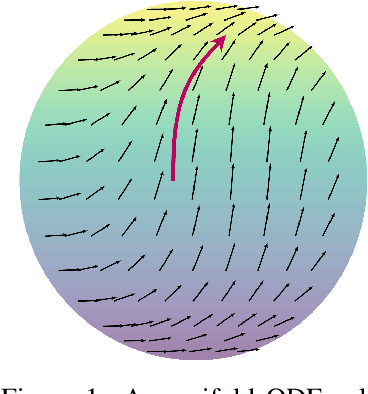
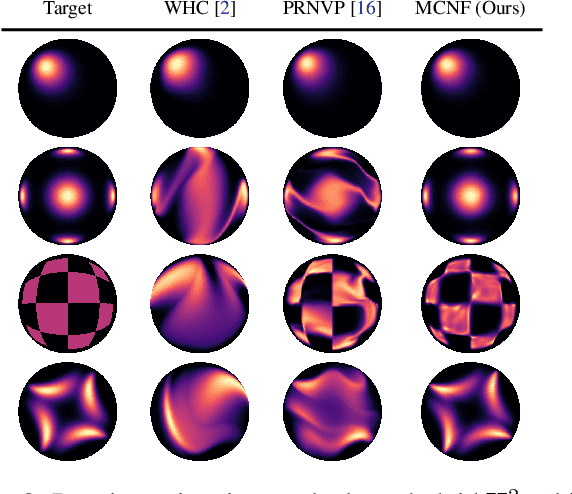
To better conform to data geometry, recent deep generative modelling techniques adapt Euclidean constructions to non-Euclidean spaces. In this paper, we study normalizing flows on manifolds. Previous work has developed flow models for specific cases; however, these advancements hand craft layers on a manifold-by-manifold basis, restricting generality and inducing cumbersome design constraints. We overcome these issues by introducing Neural Manifold Ordinary Differential Equations, a manifold generalization of Neural ODEs, which enables the construction of Manifold Continuous Normalizing Flows (MCNFs). MCNFs require only local geometry (therefore generalizing to arbitrary manifolds) and compute probabilities with continuous change of variables (allowing for a simple and expressive flow construction). We find that leveraging continuous manifold dynamics produces a marked improvement for both density estimation and downstream tasks.

Differentiating through the Fréchet Mean

Recent advances in deep representation learning on Riemannian manifolds extend classical deep learning operations to better capture the geometry of the manifold. One possible extension is the Fr\'echet mean, the generalization of the Euclidean mean; however, it has been difficult to apply because it lacks a closed form with an easily computable derivative. In this paper, we show how to differentiate through the Fr\'echet mean for arbitrary Riemannian manifolds. Then, focusing on hyperbolic space, we derive explicit gradient expressions and a fast, accurate, and hyperparameter-free Fr\'echet mean solver. This fully integrates the Fr\'echet mean into the hyperbolic neural network pipeline. To demonstrate this integration, we present two case studies. First, we apply our Fr\'echet mean to the existing Hyperbolic Graph Convolutional Network, replacing its projected aggregation to obtain state-of-the-art results on datasets with high hyperbolicity. Second, to demonstrate the Fr\'echet mean's capacity to generalize Euclidean neural network operations, we develop a hyperbolic batch normalization method that gives an improvement parallel to the one observed in the Euclidean setting.

Enhancing Adversarial Example Transferability with an Intermediate Level Attack

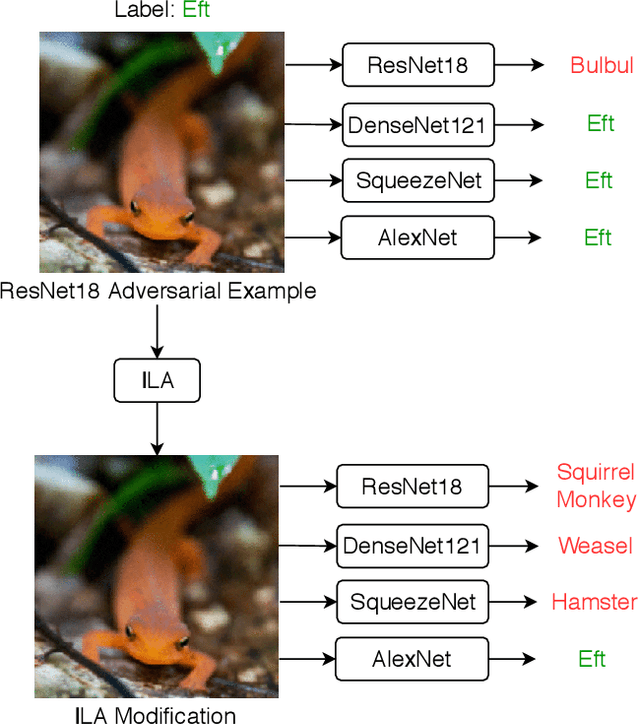
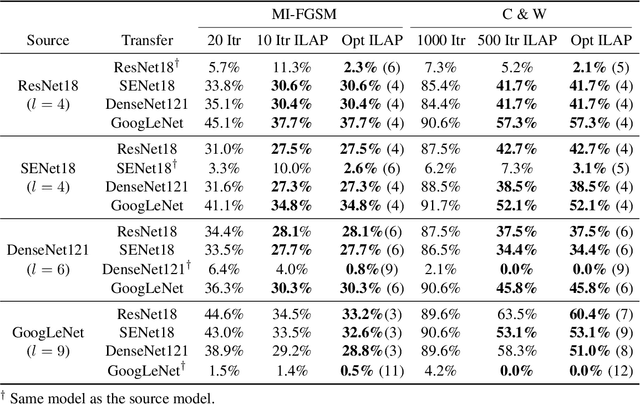
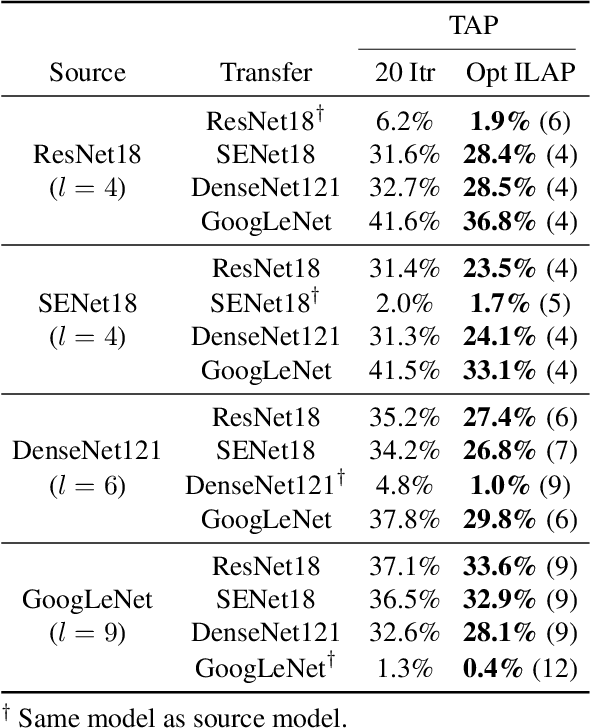
Neural networks are vulnerable to adversarial examples, malicious inputs crafted to fool trained models. Adversarial examples often exhibit black-box transfer, meaning that adversarial examples for one model can fool another model. However, adversarial examples are typically overfit to exploit the particular architecture and feature representation of a source model, resulting in sub-optimal black-box transfer attacks to other target models. We introduce the Intermediate Level Attack (ILA), which attempts to fine-tune an existing adversarial example for greater black-box transferability by increasing its perturbation on a pre-specified layer of the source model, improving upon state-of-the-art methods. We show that we can select a layer of the source model to perturb without any knowledge of the target models while achieving high transferability. Additionally, we provide some explanatory insights regarding our method and the effect of optimizing for adversarial examples in intermediate feature maps.

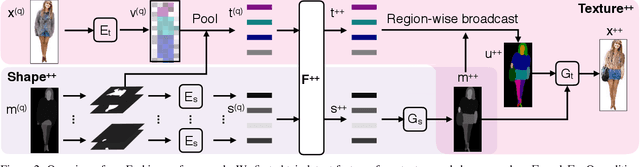
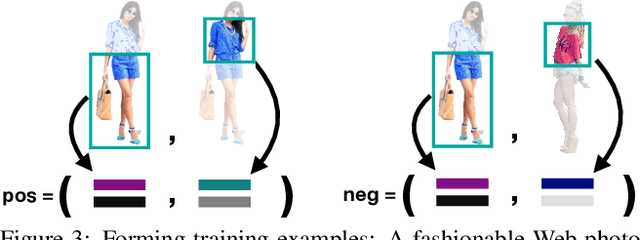
Fashion++: Minimal Edits for Outfit Improvement

Given an outfit, what small changes would most improve its fashionability? This question presents an intriguing new vision challenge. We introduce Fashion++, an approach that proposes minimal adjustments to a full-body clothing outfit that will have maximal impact on its fashionability. Our model consists of a deep image generation neural network that learns to synthesize clothing conditioned on learned per-garment encodings. The latent encodings are explicitly factorized according to shape and texture, thereby allowing direct edits for both fit/presentation and color/patterns/material, respectively. We show how to bootstrap Web photos to automatically train a fashionability model, and develop an activation maximization-style approach to transform the input image into its more fashionable self. The edits suggested range from swapping in a new garment to tweaking its color, how it is worn (e.g., rolling up sleeves), or its fit (e.g., making pants baggier). Experiments demonstrate that Fashion++ provides successful edits, both according to automated metrics and human opinion. Project page is at http://vision.cs.utexas.edu/projects/FashionPlus.

Adversarial Example Decomposition

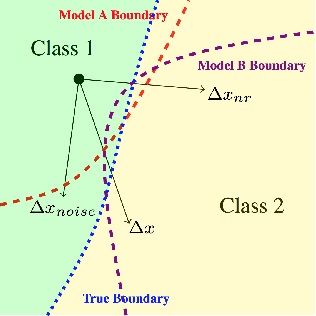
Research has shown that widely used deep neural networks are vulnerable to carefully crafted adversarial perturbations. Moreover, these adversarial perturbations often transfer across models. We hypothesize that adversarial weakness is composed of three sources of bias: architecture, dataset, and random initialization. We show that one can decompose adversarial examples into an architecture-dependent component, data-dependent component, and noise-dependent component and that these components behave intuitively. For example, noise-dependent components transfer poorly to all other models, while architecture-dependent components transfer better to retrained models with the same architecture. In addition, we demonstrate that these components can be recombined to improve transferability without sacrificing efficacy on the original model.

Intermediate Level Adversarial Attack for Enhanced Transferability

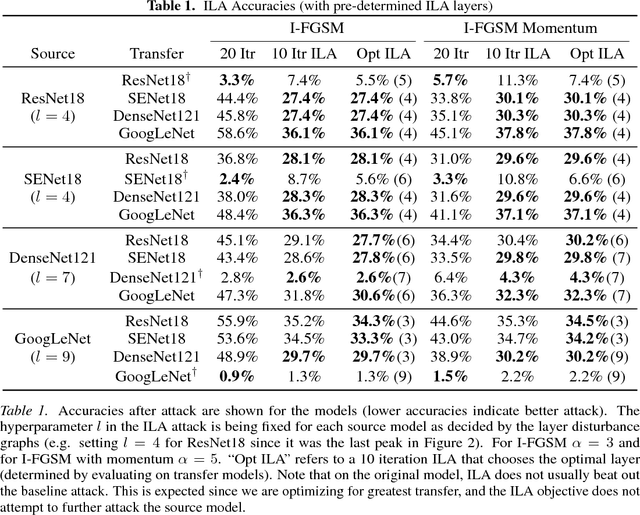
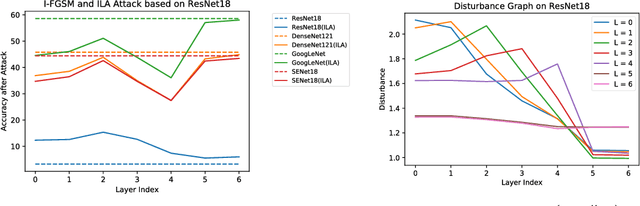
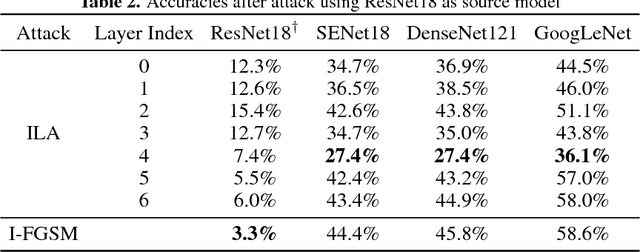
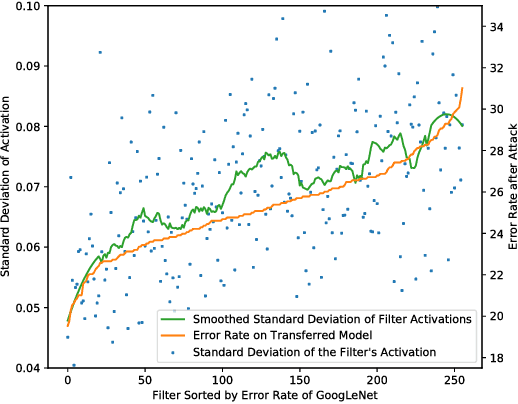
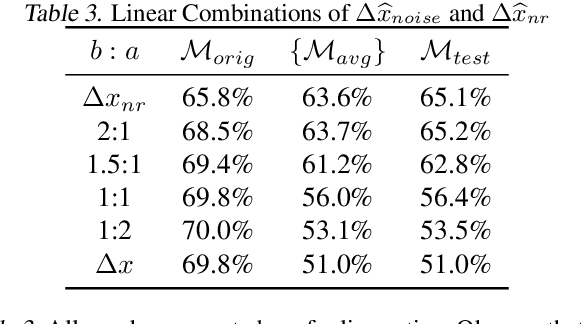
Neural networks are vulnerable to adversarial examples, malicious inputs crafted to fool trained models. Adversarial examples often exhibit black-box transfer, meaning that adversarial examples for one model can fool another model. However, adversarial examples may be overfit to exploit the particular architecture and feature representation of a source model, resulting in sub-optimal black-box transfer attacks to other target models. This leads us to introduce the Intermediate Level Attack (ILA), which attempts to fine-tune an existing adversarial example for greater black-box transferability by increasing its perturbation on a pre-specified layer of the source model. We show that our method can effectively achieve this goal and that we can decide a nearly-optimal layer of the source model to perturb without any knowledge of the target models.