Differentiating through the Fréchet Mean
Paper and Code
Mar 05, 2020


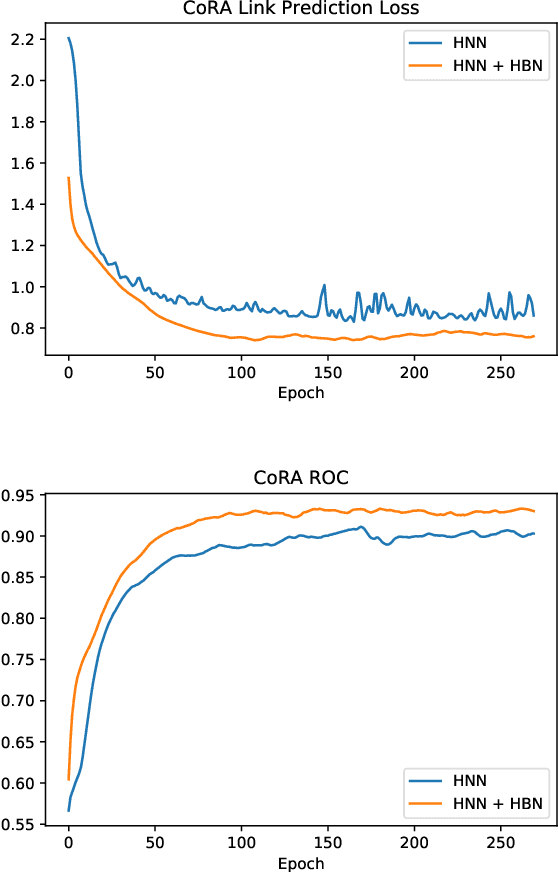
Recent advances in deep representation learning on Riemannian manifolds extend classical deep learning operations to better capture the geometry of the manifold. One possible extension is the Fr\'echet mean, the generalization of the Euclidean mean; however, it has been difficult to apply because it lacks a closed form with an easily computable derivative. In this paper, we show how to differentiate through the Fr\'echet mean for arbitrary Riemannian manifolds. Then, focusing on hyperbolic space, we derive explicit gradient expressions and a fast, accurate, and hyperparameter-free Fr\'echet mean solver. This fully integrates the Fr\'echet mean into the hyperbolic neural network pipeline. To demonstrate this integration, we present two case studies. First, we apply our Fr\'echet mean to the existing Hyperbolic Graph Convolutional Network, replacing its projected aggregation to obtain state-of-the-art results on datasets with high hyperbolicity. Second, to demonstrate the Fr\'echet mean's capacity to generalize Euclidean neural network operations, we develop a hyperbolic batch normalization method that gives an improvement parallel to the one observed in the Euclidean setting.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge