Ethan Brady
Model-assisted deep learning of rare extreme events from partial observations
Nov 04, 2021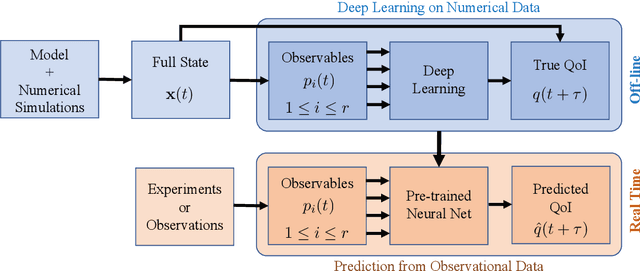
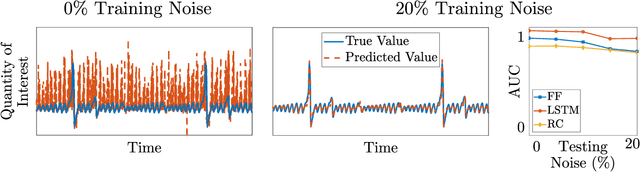
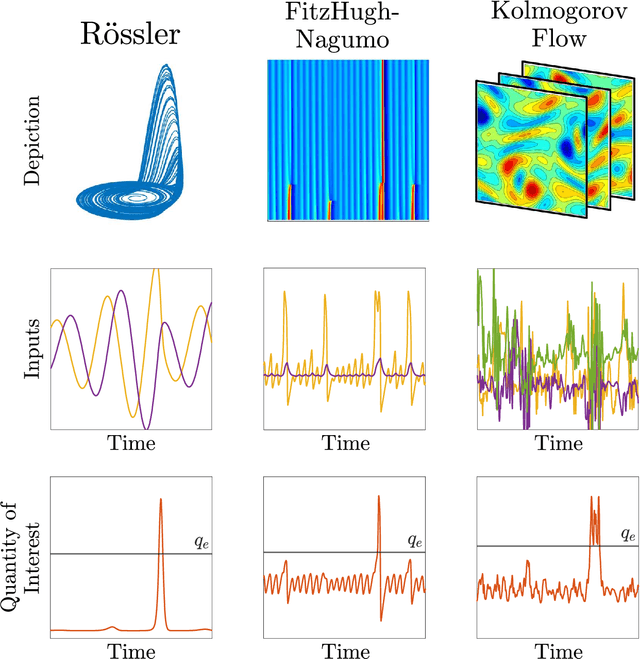
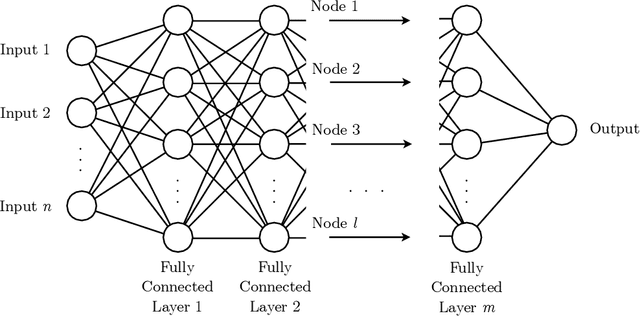
Abstract:To predict rare extreme events using deep neural networks, one encounters the so-called small data problem because even long-term observations often contain few extreme events. Here, we investigate a model-assisted framework where the training data is obtained from numerical simulations, as opposed to observations, with adequate samples from extreme events. However, to ensure the trained networks are applicable in practice, the training is not performed on the full simulation data; instead we only use a small subset of observable quantities which can be measured in practice. We investigate the feasibility of this model-assisted framework on three different dynamical systems (Rossler attractor, FitzHugh--Nagumo model, and a turbulent fluid flow) and three different deep neural network architectures (feedforward, long short-term memory, and reservoir computing). In each case, we study the prediction accuracy, robustness to noise, reproducibility under repeated training, and sensitivity to the type of input data. In particular, we find long short-term memory networks to be most robust to noise and to yield relatively accurate predictions, while requiring minimal fine-tuning of the hyperparameters.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge