State Estimation Using Sparse DEIM and Recurrent Neural Networks

Discrete Empirical Interpolation Method (DEIM) estimates a function from its pointwise incomplete observations. In particular, this method can be used to estimate the state of a dynamical system from observational data gathered by sensors. However, when the number of observations are limited, DEIM returns large estimation errors. Sparse DEIM (S-DEIM) was recently developed to address this problem by introducing a kernel vector which previous DEIM-based methods had ignored. Unfortunately, estimating the optimal kernel vector in S-DEIM is a difficult task. Here, we introduce a data-driven method to estimate this kernel vector from sparse observational time series using recurrent neural networks. Using numerical examples, we demonstrate that this machine learning approach together with S-DEIM leads to nearly optimal state estimations.

Model-assisted deep learning of rare extreme events from partial observations

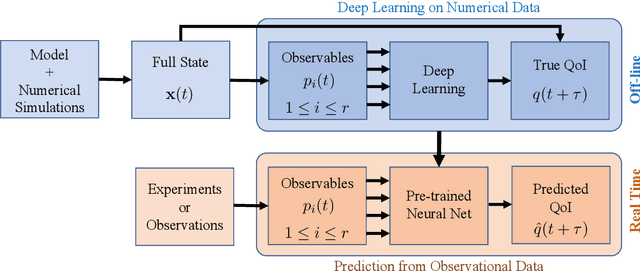
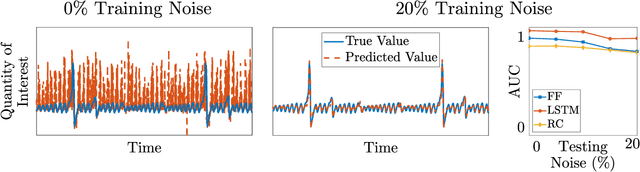
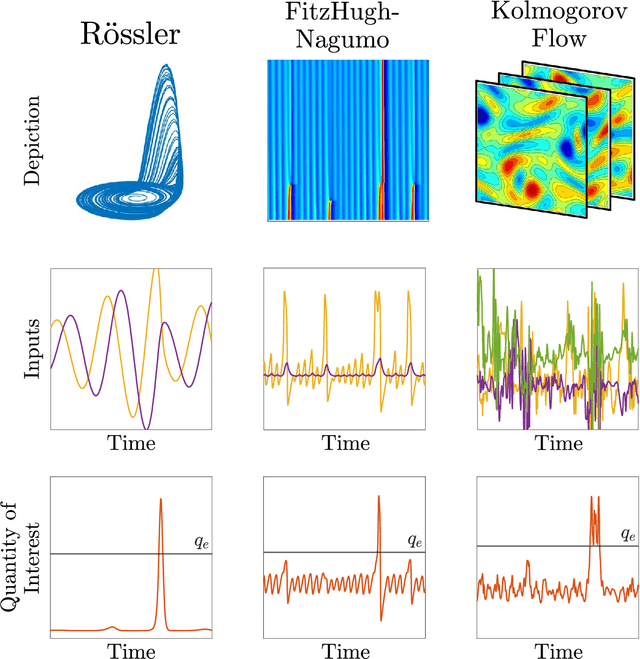
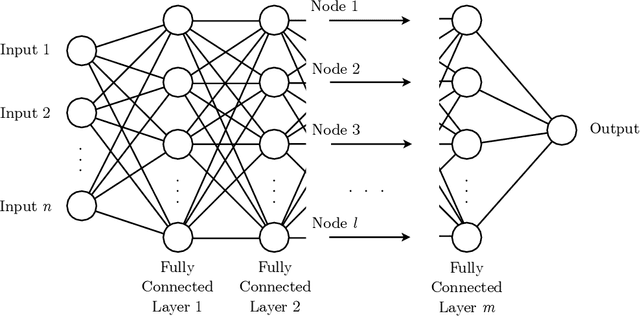
To predict rare extreme events using deep neural networks, one encounters the so-called small data problem because even long-term observations often contain few extreme events. Here, we investigate a model-assisted framework where the training data is obtained from numerical simulations, as opposed to observations, with adequate samples from extreme events. However, to ensure the trained networks are applicable in practice, the training is not performed on the full simulation data; instead we only use a small subset of observable quantities which can be measured in practice. We investigate the feasibility of this model-assisted framework on three different dynamical systems (Rossler attractor, FitzHugh--Nagumo model, and a turbulent fluid flow) and three different deep neural network architectures (feedforward, long short-term memory, and reservoir computing). In each case, we study the prediction accuracy, robustness to noise, reproducibility under repeated training, and sensitivity to the type of input data. In particular, we find long short-term memory networks to be most robust to noise and to yield relatively accurate predictions, while requiring minimal fine-tuning of the hyperparameters.

Data-driven prediction of multistable systems from sparse measurements

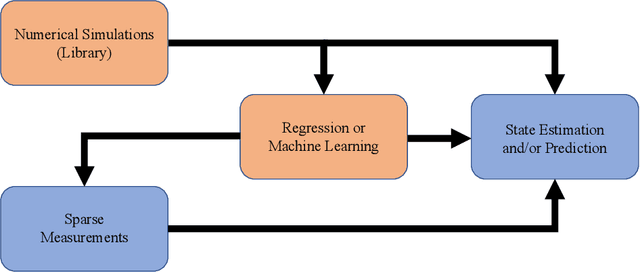
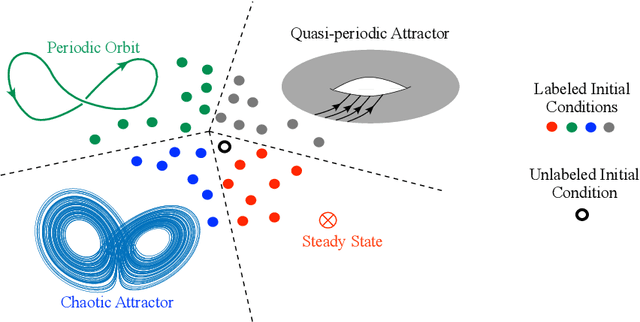
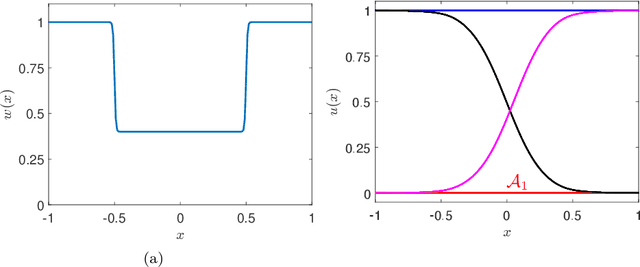
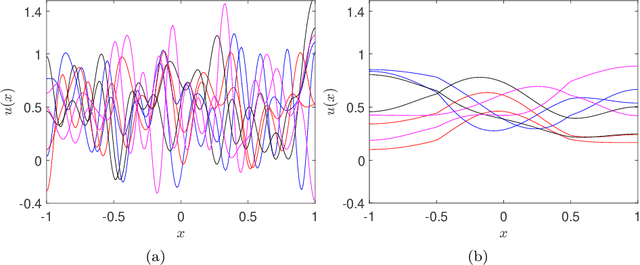
We develop a data-driven method, based on semi-supervised classification, to predict the asymptotic state of multistable systems when only sparse spatial measurements of the system are feasible. Our method predicts the asymptotic behavior of an observed state by quantifying its proximity to the states in a precomputed library of data. To quantify this proximity, we introduce a sparsity-promoting metric-learning (SPML) optimization, which learns a metric directly from the precomputed data. The resulting metric has two important properties: (i) It is compatible with the precomputed library, and (ii) It is computable from sparse measurements. We demonstrate the application of this method on a multistable reaction-diffusion equation which has four asymptotically stable steady states. Classifications based on SPML predict the asymptotic behavior of initial conditions, based on two-point measurements, with over $89\%$ accuracy. The learned optimal metric also determines where these measurements need to be made to ensure accurate predictions.