A Kernel-Based Conditional Two-Sample Test Using Nearest Neighbors (with Applications to Calibration, Regression Curves, and Simulation-Based Inference)

In this paper we introduce a kernel-based measure for detecting differences between two conditional distributions. Using the `kernel trick' and nearest-neighbor graphs, we propose a consistent estimate of this measure which can be computed in nearly linear time (for a fixed number of nearest neighbors). Moreover, when the two conditional distributions are the same, the estimate has a Gaussian limit and its asymptotic variance has a simple form that can be easily estimated from the data. The resulting test attains precise asymptotic level and is universally consistent for detecting differences between two conditional distributions. We also provide a resampling based test using our estimate that applies to the conditional goodness-of-fit problem, which controls Type I error in finite samples and is asymptotically consistent with only a finite number of resamples. A method to de-randomize the resampling test is also presented. The proposed methods can be readily applied to a broad range of problems, ranging from classical nonparametric statistics to modern machine learning. Specifically, we explore three applications: testing model calibration, regression curve evaluation, and validation of emulator models in simulation-based inference. We illustrate the superior performance of our method for these tasks, both in simulations as well as on real data. In particular, we apply our method to (1) assess the calibration of neural network models trained on the CIFAR-10 dataset, (2) compare regression functions for wind power generation across two different turbines, and (3) validate emulator models on benchmark examples with intractable posteriors and for generating synthetic `redshift' associated with galaxy images.

Degree Heterogeneity in Higher-Order Networks: Inference in the Hypergraph $\boldsymbolβ$-Model

The $\boldsymbol{\beta}$-model for random graphs is commonly used for representing pairwise interactions in a network with degree heterogeneity. Going beyond pairwise interactions, Stasi et al. (2014) introduced the hypergraph $\boldsymbol{\beta}$-model for capturing degree heterogeneity in networks with higher-order (multi-way) interactions. In this paper we initiate the rigorous study of the hypergraph $\boldsymbol{\beta}$-model with multiple layers, which allows for hyperedges of different sizes across the layers. To begin with, we derive the rates of convergence of the maximum likelihood (ML) estimate and establish their minimax rate optimality. We also derive the limiting distribution of the ML estimate and construct asymptotically valid confidence intervals for the model parameters. Next, we consider the goodness-of-fit problem in the hypergraph $\boldsymbol{\beta}$-model. Specifically, we establish the asymptotic normality of the likelihood ratio (LR) test under the null hypothesis, derive its detection threshold, and also its limiting power at the threshold. Interestingly, the detection threshold of the LR test turns out to be minimax optimal, that is, all tests are asymptotically powerless below this threshold. The theoretical results are further validated in numerical experiments. In addition to developing the theoretical framework for estimation and inference for hypergraph $\boldsymbol{\beta}$-models, the above results fill a number of gaps in the graph $\boldsymbol{\beta}$-model literature, such as the minimax optimality of the ML estimates and the non-null properties of the LR test, which, to the best of our knowledge, have not been studied before.

Bootstrapped Edge Count Tests for Nonparametric Two-Sample Inference Under Heterogeneity

Nonparametric two-sample testing is a classical problem in inferential statistics. While modern two-sample tests, such as the edge count test and its variants, can handle multivariate and non-Euclidean data, contemporary gargantuan datasets often exhibit heterogeneity due to the presence of latent subpopulations. Direct application of these tests, without regulating for such heterogeneity, may lead to incorrect statistical decisions. We develop a new nonparametric testing procedure that accurately detects differences between the two samples in the presence of unknown heterogeneity in the data generation process. Our framework handles this latent heterogeneity through a composite null that entertains the possibility that the two samples arise from a mixture distribution with identical component distributions but with possibly different mixing weights. In this regime, we study the asymptotic behavior of weighted edge count test statistic and show that it can be effectively re-calibrated to detect arbitrary deviations from the composite null. For practical implementation we propose a Bootstrapped Weighted Edge Count test which involves a bootstrap-based calibration procedure that can be easily implemented across a wide range of heterogeneous regimes. A comprehensive simulation study and an application to detecting aberrant user behaviors in online games demonstrates the excellent non-asymptotic performance of the proposed test.

Boosting the Power of Kernel Two-Sample Tests

The kernel two-sample test based on the maximum mean discrepancy (MMD) is one of the most popular methods for detecting differences between two distributions over general metric spaces. In this paper we propose a method to boost the power of the kernel test by combining MMD estimates over multiple kernels using their Mahalanobis distance. We derive the asymptotic null distribution of the proposed test statistic and use a multiplier bootstrap approach to efficiently compute the rejection region. The resulting test is universally consistent and, since it is obtained by aggregating over a collection of kernels/bandwidths, is more powerful in detecting a wide range of alternatives in finite samples. We also derive the distribution of the test statistic for both fixed and local contiguous alternatives. The latter, in particular, implies that the proposed test is statistically efficient, that is, it has non-trivial asymptotic (Pitman) efficiency. Extensive numerical experiments are performed on both synthetic and real-world datasets to illustrate the efficacy of the proposed method over single kernel tests. Our asymptotic results rely on deriving the joint distribution of MMD estimates using the framework of multiple stochastic integrals, which is more broadly useful, specifically, in understanding the efficiency properties of recently proposed adaptive MMD tests based on kernel aggregation.

Estimation in Tensor Ising Models

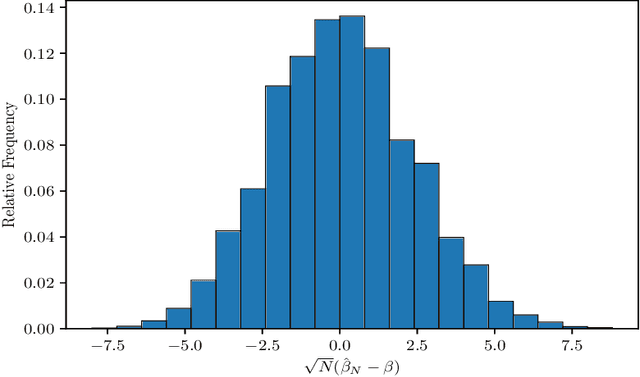
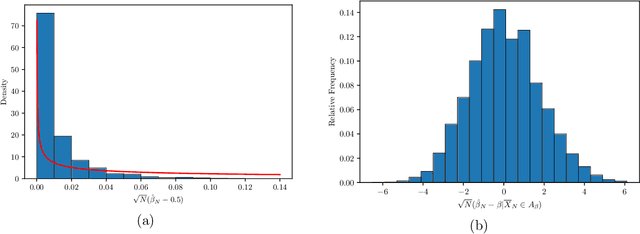
The $p$-tensor Ising model is a one-parameter discrete exponential family for modeling dependent binary data, where the sufficient statistic is a multi-linear form of degree $p \geq 2$. This is a natural generalization of the matrix Ising model, that provides a convenient mathematical framework for capturing higher-order dependencies in complex relational data. In this paper, we consider the problem of estimating the natural parameter of the $p$-tensor Ising model given a single sample from the distribution on $N$ nodes. Our estimate is based on the maximum pseudo-likelihood (MPL) method, which provides a computationally efficient algorithm for estimating the parameter that avoids computing the intractable partition function. We derive general conditions under which the MPL estimate is $\sqrt N$-consistent, that is, it converges to the true parameter at rate $1/\sqrt N$. In particular, we show the $\sqrt N$-consistency of the MPL estimate in the $p$-spin Sherrington-Kirkpatrick (SK) model, spin systems on general $p$-uniform hypergraphs, and Ising models on the hypergraph stochastic block model (HSBM). In fact, for the HSBM we pin down the exact location of the phase transition threshold, which is determined by the positivity of a certain mean-field variational problem, such that above this threshold the MPL estimate is $\sqrt N$-consistent, while below the threshold no estimator is consistent. Finally, we derive the precise fluctuations of the MPL estimate in the special case of the $p$-tensor Curie-Weiss model. An interesting consequence of our results is that the MPL estimate in the Curie-Weiss model saturates the Cramer-Rao lower bound at all points above the estimation threshold, that is, the MPL estimate incurs no loss in asymptotic efficiency, even though it is obtained by minimizing only an approximation of the true likelihood function for computational tractability.

Testing Closeness With Unequal Sized Samples

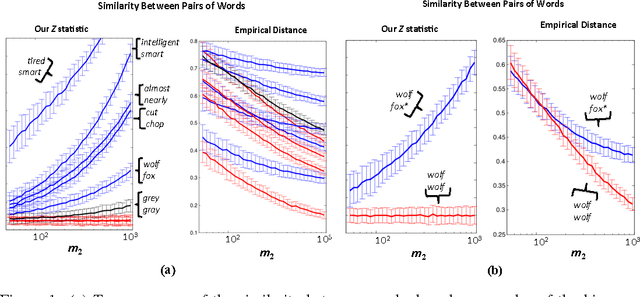
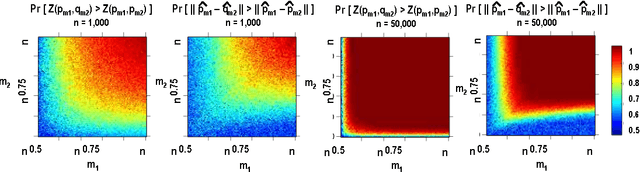
We consider the problem of closeness testing for two discrete distributions in the practically relevant setting of \emph{unequal} sized samples drawn from each of them. Specifically, given a target error parameter $\varepsilon > 0$, $m_1$ independent draws from an unknown distribution $p,$ and $m_2$ draws from an unknown distribution $q$, we describe a test for distinguishing the case that $p=q$ from the case that $||p-q||_1 \geq \varepsilon$. If $p$ and $q$ are supported on at most $n$ elements, then our test is successful with high probability provided $m_1\geq n^{2/3}/\varepsilon^{4/3}$ and $m_2 = \Omega(\max\{\frac{n}{\sqrt m_1\varepsilon^2}, \frac{\sqrt n}{\varepsilon^2}\});$ we show that this tradeoff is optimal throughout this range, to constant factors. These results extend the recent work of Chan et al. who established the sample complexity when the two samples have equal sizes, and tightens the results of Acharya et al. by polynomials factors in both $n$ and $\varepsilon$. As a consequence, we obtain an algorithm for estimating the mixing time of a Markov chain on $n$ states up to a $\log n$ factor that uses $\tilde{O}(n^{3/2} \tau_{mix})$ queries to a "next node" oracle, improving upon the $\tilde{O}(n^{5/3}\tau_{mix})$ query algorithm of Batu et al. Finally, we note that the core of our testing algorithm is a relatively simple statistic that seems to perform well in practice, both on synthetic data and on natural language data.