Empirical Bayes Estimation with Side Information: A Nonparametric Integrative Tweedie Approach

We investigate the problem of compound estimation of normal means while accounting for the presence of side information. Leveraging the empirical Bayes framework, we develop a nonparametric integrative Tweedie (NIT) approach that incorporates structural knowledge encoded in multivariate auxiliary data to enhance the precision of compound estimation. Our approach employs convex optimization tools to estimate the gradient of the log-density directly, enabling the incorporation of structural constraints. We conduct theoretical analyses of the asymptotic risk of NIT and establish the rate at which NIT converges to the oracle estimator. As the dimension of the auxiliary data increases, we accurately quantify the improvements in estimation risk and the associated deterioration in convergence rate. The numerical performance of NIT is illustrated through the analysis of both simulated and real data, demonstrating its superiority over existing methods.

Bootstrapped Edge Count Tests for Nonparametric Two-Sample Inference Under Heterogeneity

Nonparametric two-sample testing is a classical problem in inferential statistics. While modern two-sample tests, such as the edge count test and its variants, can handle multivariate and non-Euclidean data, contemporary gargantuan datasets often exhibit heterogeneity due to the presence of latent subpopulations. Direct application of these tests, without regulating for such heterogeneity, may lead to incorrect statistical decisions. We develop a new nonparametric testing procedure that accurately detects differences between the two samples in the presence of unknown heterogeneity in the data generation process. Our framework handles this latent heterogeneity through a composite null that entertains the possibility that the two samples arise from a mixture distribution with identical component distributions but with possibly different mixing weights. In this regime, we study the asymptotic behavior of weighted edge count test statistic and show that it can be effectively re-calibrated to detect arbitrary deviations from the composite null. For practical implementation we propose a Bootstrapped Weighted Edge Count test which involves a bootstrap-based calibration procedure that can be easily implemented across a wide range of heterogeneous regimes. A comprehensive simulation study and an application to detecting aberrant user behaviors in online games demonstrates the excellent non-asymptotic performance of the proposed test.

Rethinking gradient sparsification as total error minimization

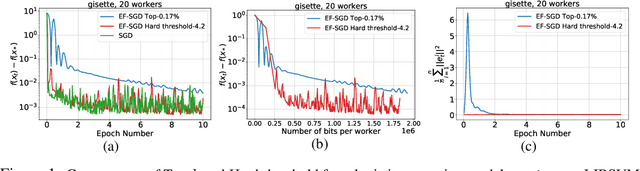
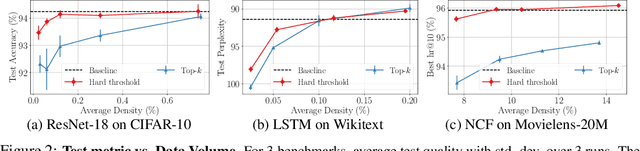
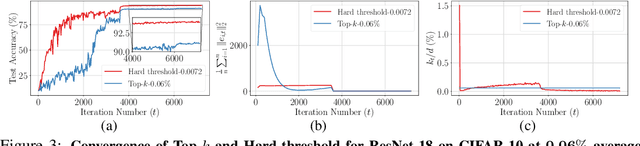
Gradient compression is a widely-established remedy to tackle the communication bottleneck in distributed training of large deep neural networks (DNNs). Under the error-feedback framework, Top-$k$ sparsification, sometimes with $k$ as little as $0.1\%$ of the gradient size, enables training to the same model quality as the uncompressed case for a similar iteration count. From the optimization perspective, we find that Top-$k$ is the communication-optimal sparsifier given a per-iteration $k$ element budget. We argue that to further the benefits of gradient sparsification, especially for DNNs, a different perspective is necessary -- one that moves from per-iteration optimality to consider optimality for the entire training. We identify that the total error -- the sum of the compression errors for all iterations -- encapsulates sparsification throughout training. Then, we propose a communication complexity model that minimizes the total error under a communication budget for the entire training. We find that the hard-threshold sparsifier, a variant of the Top-$k$ sparsifier with $k$ determined by a constant hard-threshold, is the optimal sparsifier for this model. Motivated by this, we provide convex and non-convex convergence analyses for the hard-threshold sparsifier with error-feedback. Unlike with Top-$k$ sparsifier, we show that hard-threshold has the same asymptotic convergence and linear speedup property as SGD in the convex case and has no impact on the data-heterogeneity in the non-convex case. Our diverse experiments on various DNNs and a logistic regression model demonstrated that the hard-threshold sparsifier is more communication-efficient than Top-$k$.