Robust Online Conformal Prediction under Uniform Label Noise

Conformal prediction is an emerging technique for uncertainty quantification that constructs prediction sets guaranteed to contain the true label with a predefined probability. Recent work develops online conformal prediction methods that adaptively construct prediction sets to accommodate distribution shifts. However, existing algorithms typically assume perfect label accuracy which rarely holds in practice. In this work, we investigate the robustness of online conformal prediction under uniform label noise with a known noise rate, in both constant and dynamic learning rate schedules. We show that label noise causes a persistent gap between the actual mis-coverage rate and the desired rate $\alpha$, leading to either overestimated or underestimated coverage guarantees. To address this issue, we propose Noise Robust Online Conformal Prediction (dubbed NR-OCP) by updating the threshold with a novel robust pinball los}, which provides an unbiased estimate of clean pinball loss without requiring ground-truth labels. Our theoretical analysis shows that NR-OCP eliminates the coverage gap in both constant and dynamic learning rate schedules, achieving a convergence rate of $\mathcal{O}(T^{-1/2})$ for both empirical and expected coverage errors under uniform label noise. Extensive experiments demonstrate the effectiveness of our method by achieving both precise coverage and improved efficiency.

Cotton Yield Prediction Using Random Forest

The cotton industry in the United States is committed to sustainable production practices that minimize water, land, and energy use while improving soil health and cotton output. Climate-smart agricultural technologies are being developed to boost yields while decreasing operating expenses. Crop yield prediction, on the other hand, is difficult because of the complex and nonlinear impacts of cultivar, soil type, management, pest and disease, climate, and weather patterns on crops. To solve this issue, we employ machine learning (ML) to forecast production while considering climate change, soil diversity, cultivar, and inorganic nitrogen levels. From the 1980s to the 1990s, field data were gathered across the southern cotton belt of the United States. To capture the most current effects of climate change over the previous six years, a second data source was produced using the process-based crop model, GOSSYM. We concentrated our efforts on three distinct areas inside each of the three southern states: Texas, Mississippi, and Georgia. To simplify the amount of computations, accumulated heat units (AHU) for each set of experimental data were employed as an analogy to use time-series weather data. The Random Forest Regressor yielded a 97.75% accuracy rate, with a root mean square error of 55.05 kg/ha and an R2 of around 0.98. These findings demonstrate how an ML technique may be developed and applied as a reliable and easy-to-use model to support the cotton climate-smart initiative.

Empirical Bayes Estimation with Side Information: A Nonparametric Integrative Tweedie Approach

We investigate the problem of compound estimation of normal means while accounting for the presence of side information. Leveraging the empirical Bayes framework, we develop a nonparametric integrative Tweedie (NIT) approach that incorporates structural knowledge encoded in multivariate auxiliary data to enhance the precision of compound estimation. Our approach employs convex optimization tools to estimate the gradient of the log-density directly, enabling the incorporation of structural constraints. We conduct theoretical analyses of the asymptotic risk of NIT and establish the rate at which NIT converges to the oracle estimator. As the dimension of the auxiliary data increases, we accurately quantify the improvements in estimation risk and the associated deterioration in convergence rate. The numerical performance of NIT is illustrated through the analysis of both simulated and real data, demonstrating its superiority over existing methods.

Integrative conformal p-values for powerful out-of-distribution testing with labeled outliers

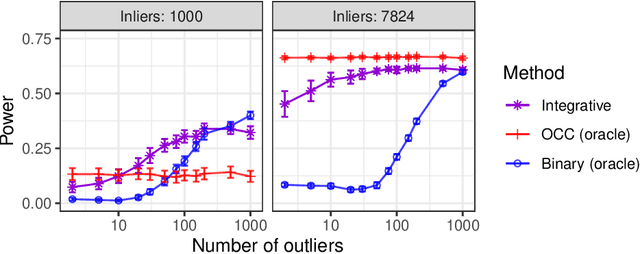
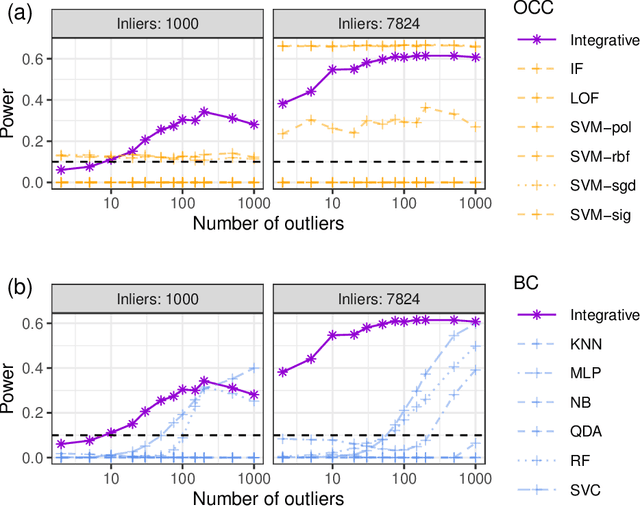
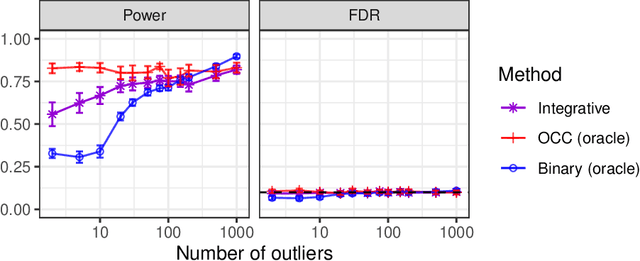
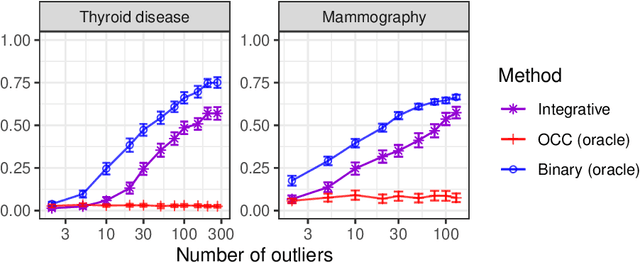
This paper develops novel conformal methods to test whether a new observation was sampled from the same distribution as a reference set. Blending inductive and transductive conformal inference in an innovative way, the described methods can re-weight standard conformal p-values based on dependent side information from known out-of-distribution data in a principled way, and can automatically take advantage of the most powerful model from any collection of one-class and binary classifiers. The solution can be implemented either through sample splitting or via a novel transductive cross-validation+ scheme which may also be useful in other applications of conformal inference, due to tighter guarantees compared to existing cross-validation approaches. After studying false discovery rate control and power within a multiple testing framework with several possible outliers, the proposed solution is shown to outperform standard conformal p-values through simulations as well as applications to image recognition and tabular data.

Locally Adaptive Transfer Learning Algorithms for Large-Scale Multiple Testing

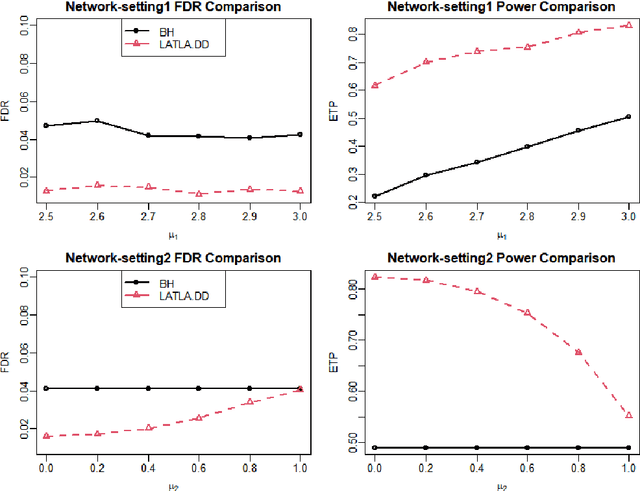
Transfer learning has enjoyed increasing popularity in a range of big data applications. In the context of large-scale multiple testing, the goal is to extract and transfer knowledge learned from related source domains to improve the accuracy of simultaneously testing of a large number of hypotheses in the target domain. This article develops a locally adaptive transfer learning algorithm (LATLA) for transfer learning for multiple testing. In contrast with existing covariate-assisted multiple testing methods that require the auxiliary covariates to be collected alongside the primary data on the same testing units, LATLA provides a principled and generic transfer learning framework that is capable of incorporating multiple samples of auxiliary data from related source domains, possibly in different dimensions/structures and from diverse populations. Both the theoretical and numerical results show that LATLA controls the false discovery rate and outperforms existing methods in power. LATLA is illustrated through an application to genome-wide association studies for the identification of disease-associated SNPs by cross-utilizing the auxiliary data from a related linkage analysis.

Large-Scale Shrinkage Estimation under Markovian Dependence

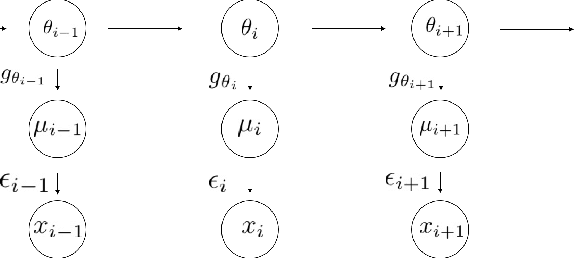
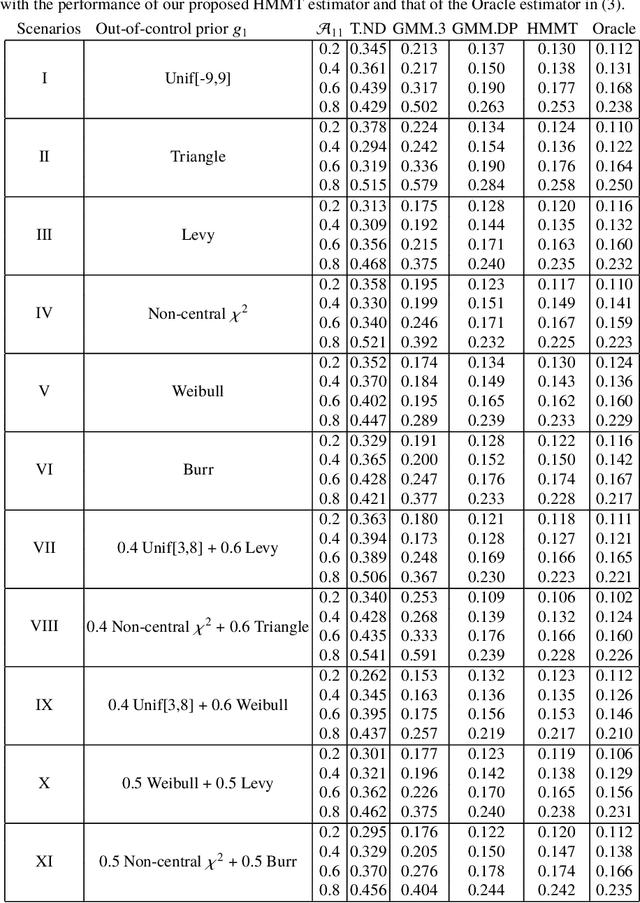
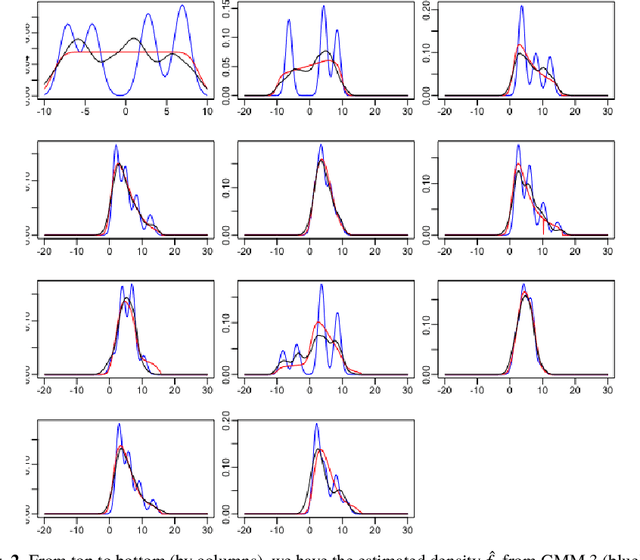
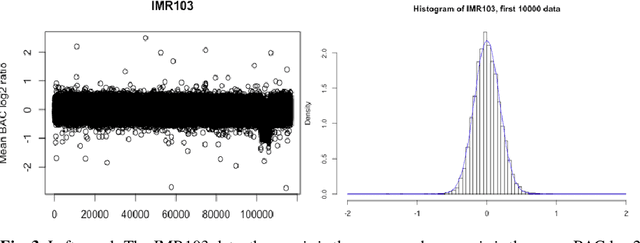
We consider the problem of simultaneous estimation of a sequence of dependent parameters that are generated from a hidden Markov model. Based on observing a noise contaminated vector of observations from such a sequence model, we consider simultaneous estimation of all the parameters irrespective of their hidden states under square error loss. We study the roles of statistical shrinkage for improved estimation of these dependent parameters. Being completely agnostic on the distributional properties of the unknown underlying Hidden Markov model, we develop a novel non-parametric shrinkage algorithm. Our proposed method elegantly combines \textit{Tweedie}-based non-parametric shrinkage ideas with efficient estimation of the hidden states under Markovian dependence. Based on extensive numerical experiments, we establish superior performance our our proposed algorithm compared to non-shrinkage based state-of-the-art parametric as well as non-parametric algorithms used in hidden Markov models. We provide decision theoretic properties of our methodology and exhibit its enhanced efficacy over popular shrinkage methods built under independence. We demonstrate the application of our methodology on real-world datasets for analyzing of temporally dependent social and economic indicators such as search trends and unemployment rates as well as estimating spatially dependent Copy Number Variations.

Structure-Adaptive Sequential Testing for Online False Discovery Rate Control

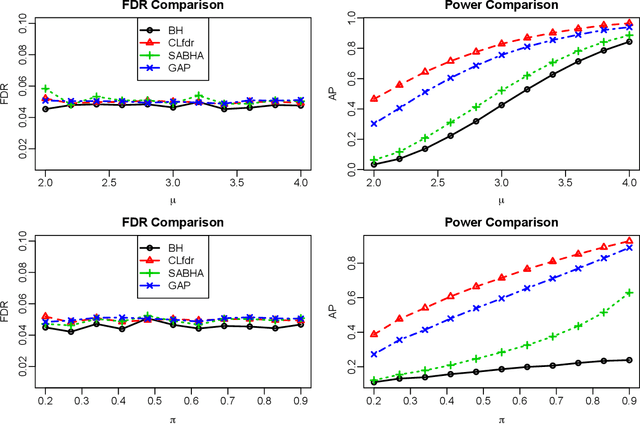
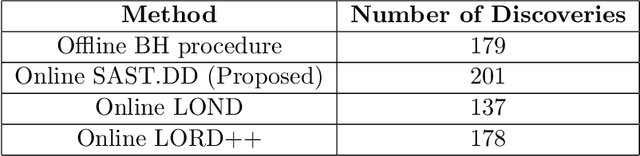
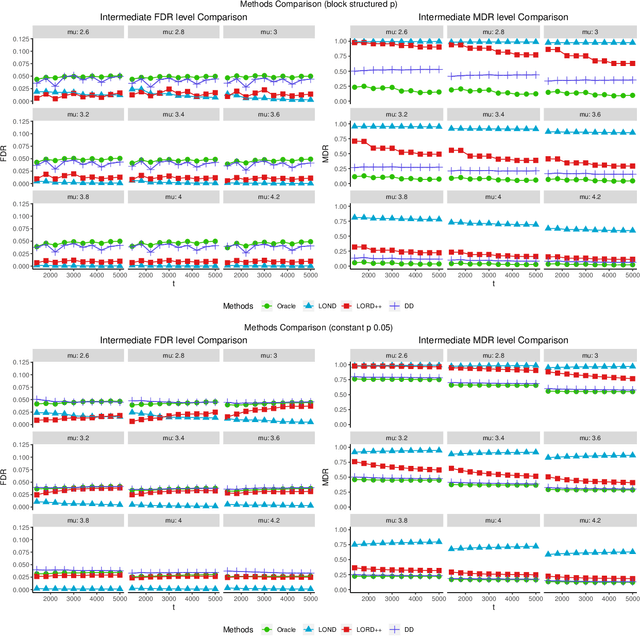
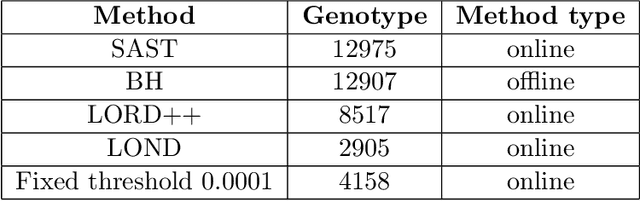
Consider the online testing of a stream of hypotheses where a real--time decision must be made before the next data point arrives. The error rate is required to be controlled at {all} decision points. Conventional \emph{simultaneous testing rules} are no longer applicable due to the more stringent error constraints and absence of future data. Moreover, the online decision--making process may come to a halt when the total error budget, or alpha--wealth, is exhausted. This work develops a new class of structure--adaptive sequential testing (SAST) rules for online false discover rate (FDR) control. A key element in our proposal is a new alpha--investment algorithm that precisely characterizes the gains and losses in sequential decision making. SAST captures time varying structures of the data stream, learns the optimal threshold adaptively in an ongoing manner and optimizes the alpha-wealth allocation across different time periods. We present theory and numerical results to show that the proposed method is valid for online FDR control and achieves substantial power gain over existing online testing rules.