Federated PCA and Estimation for Spiked Covariance Matrices: Optimal Rates and Efficient Algorithm

Federated Learning (FL) has gained significant recent attention in machine learning for its enhanced privacy and data security, making it indispensable in fields such as healthcare, finance, and personalized services. This paper investigates federated PCA and estimation for spiked covariance matrices under distributed differential privacy constraints. We establish minimax rates of convergence, with a key finding that the central server's optimal rate is the harmonic mean of the local clients' minimax rates. This guarantees consistent estimation at the central server as long as at least one local client provides consistent results. Notably, consistency is maintained even if some local estimators are inconsistent, provided there are enough clients. These findings highlight the robustness and scalability of FL for reliable statistical inference under privacy constraints. To establish minimax lower bounds, we derive a matrix version of van Trees' inequality, which is of independent interest. Furthermore, we propose an efficient algorithm that preserves differential privacy while achieving near-optimal rates at the central server, up to a logarithmic factor. We address significant technical challenges in analyzing this algorithm, which involves a three-layer spectral decomposition. Numerical performance of the proposed algorithm is investigated using both simulated and real data.

Minimax And Adaptive Transfer Learning for Nonparametric Classification under Distributed Differential Privacy Constraints

This paper considers minimax and adaptive transfer learning for nonparametric classification under the posterior drift model with distributed differential privacy constraints. Our study is conducted within a heterogeneous framework, encompassing diverse sample sizes, varying privacy parameters, and data heterogeneity across different servers. We first establish the minimax misclassification rate, precisely characterizing the effects of privacy constraints, source samples, and target samples on classification accuracy. The results reveal interesting phase transition phenomena and highlight the intricate trade-offs between preserving privacy and achieving classification accuracy. We then develop a data-driven adaptive classifier that achieves the optimal rate within a logarithmic factor across a large collection of parameter spaces while satisfying the same set of differential privacy constraints. Simulation studies and real-world data applications further elucidate the theoretical analysis with numerical results.

Optimal Federated Learning for Nonparametric Regression with Heterogeneous Distributed Differential Privacy Constraints

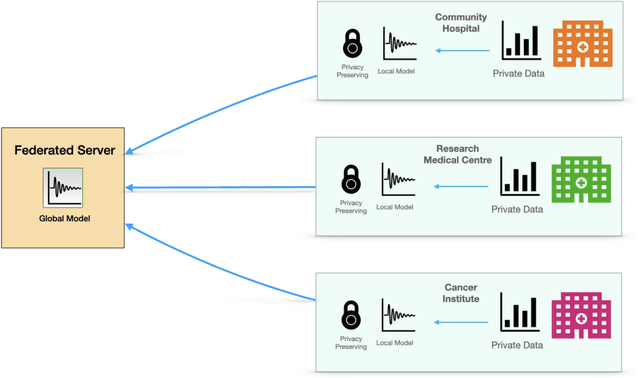
This paper studies federated learning for nonparametric regression in the context of distributed samples across different servers, each adhering to distinct differential privacy constraints. The setting we consider is heterogeneous, encompassing both varying sample sizes and differential privacy constraints across servers. Within this framework, both global and pointwise estimation are considered, and optimal rates of convergence over the Besov spaces are established. Distributed privacy-preserving estimators are proposed and their risk properties are investigated. Matching minimax lower bounds, up to a logarithmic factor, are established for both global and pointwise estimation. Together, these findings shed light on the tradeoff between statistical accuracy and privacy preservation. In particular, we characterize the compromise not only in terms of the privacy budget but also concerning the loss incurred by distributing data within the privacy framework as a whole. This insight captures the folklore wisdom that it is easier to retain privacy in larger samples, and explores the differences between pointwise and global estimation under distributed privacy constraints.

Federated Nonparametric Hypothesis Testing with Differential Privacy Constraints: Optimal Rates and Adaptive Tests

Federated learning has attracted significant recent attention due to its applicability across a wide range of settings where data is collected and analyzed across disparate locations. In this paper, we study federated nonparametric goodness-of-fit testing in the white-noise-with-drift model under distributed differential privacy (DP) constraints. We first establish matching lower and upper bounds, up to a logarithmic factor, on the minimax separation rate. This optimal rate serves as a benchmark for the difficulty of the testing problem, factoring in model characteristics such as the number of observations, noise level, and regularity of the signal class, along with the strictness of the $(\epsilon,\delta)$-DP requirement. The results demonstrate interesting and novel phase transition phenomena. Furthermore, the results reveal an interesting phenomenon that distributed one-shot protocols with access to shared randomness outperform those without access to shared randomness. We also construct a data-driven testing procedure that possesses the ability to adapt to an unknown regularity parameter over a large collection of function classes with minimal additional cost, all while maintaining adherence to the same set of DP constraints.

Transfer Learning for Nonparametric Regression: Non-asymptotic Minimax Analysis and Adaptive Procedure

Transfer learning for nonparametric regression is considered. We first study the non-asymptotic minimax risk for this problem and develop a novel estimator called the confidence thresholding estimator, which is shown to achieve the minimax optimal risk up to a logarithmic factor. Our results demonstrate two unique phenomena in transfer learning: auto-smoothing and super-acceleration, which differentiate it from nonparametric regression in a traditional setting. We then propose a data-driven algorithm that adaptively achieves the minimax risk up to a logarithmic factor across a wide range of parameter spaces. Simulation studies are conducted to evaluate the numerical performance of the adaptive transfer learning algorithm, and a real-world example is provided to demonstrate the benefits of the proposed method.

Optimal Differentially Private PCA and Estimation for Spiked Covariance Matrices

Estimating a covariance matrix and its associated principal components is a fundamental problem in contemporary statistics. While optimal estimation procedures have been developed with well-understood properties, the increasing demand for privacy preservation introduces new complexities to this classical problem. In this paper, we study optimal differentially private Principal Component Analysis (PCA) and covariance estimation within the spiked covariance model. We precisely characterize the sensitivity of eigenvalues and eigenvectors under this model and establish the minimax rates of convergence for estimating both the principal components and covariance matrix. These rates hold up to logarithmic factors and encompass general Schatten norms, including spectral norm, Frobenius norm, and nuclear norm as special cases. We introduce computationally efficient differentially private estimators and prove their minimax optimality, up to logarithmic factors. Additionally, matching minimax lower bounds are established. Notably, in comparison with existing literature, our results accommodate a diverging rank, necessitate no eigengap condition between distinct principal components, and remain valid even if the sample size is much smaller than the dimension.

Score Attack: A Lower Bound Technique for Optimal Differentially Private Learning

Achieving optimal statistical performance while ensuring the privacy of personal data is a challenging yet crucial objective in modern data analysis. However, characterizing the optimality, particularly the minimax lower bound, under privacy constraints is technically difficult. To address this issue, we propose a novel approach called the score attack, which provides a lower bound on the differential-privacy-constrained minimax risk of parameter estimation. The score attack method is based on the tracing attack concept in differential privacy and can be applied to any statistical model with a well-defined score statistic. It can optimally lower bound the minimax risk of estimating unknown model parameters, up to a logarithmic factor, while ensuring differential privacy for a range of statistical problems. We demonstrate the effectiveness and optimality of this general method in various examples, such as the generalized linear model in both classical and high-dimensional sparse settings, the Bradley-Terry-Luce model for pairwise comparisons, and nonparametric regression over the Sobolev class.

Testing High-dimensional Multinomials with Applications to Text Analysis

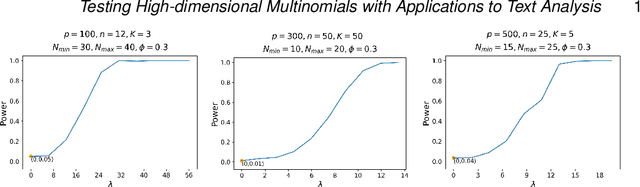
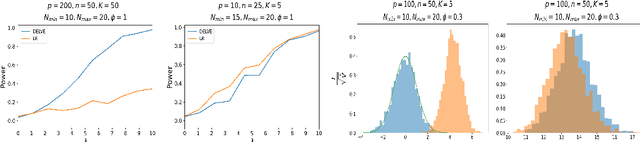
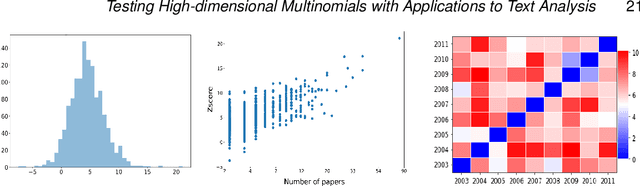
Motivated by applications in text mining and discrete distribution inference, we investigate the testing for equality of probability mass functions of $K$ groups of high-dimensional multinomial distributions. A test statistic, which is shown to have an asymptotic standard normal distribution under the null, is proposed. The optimal detection boundary is established, and the proposed test is shown to achieve this optimal detection boundary across the entire parameter space of interest. The proposed method is demonstrated in simulation studies and applied to analyze two real-world datasets to examine variation among consumer reviews of Amazon movies and diversity of statistical paper abstracts.

Transfer Learning for Contextual Multi-armed Bandits

Motivated by a range of applications, we study in this paper the problem of transfer learning for nonparametric contextual multi-armed bandits under the covariate shift model, where we have data collected on source bandits before the start of the target bandit learning. The minimax rate of convergence for the cumulative regret is established and a novel transfer learning algorithm that attains the minimax regret is proposed. The results quantify the contribution of the data from the source domains for learning in the target domain in the context of nonparametric contextual multi-armed bandits. In view of the general impossibility of adaptation to unknown smoothness, we develop a data-driven algorithm that achieves near-optimal statistical guarantees (up to a logarithmic factor) while automatically adapting to the unknown parameters over a large collection of parameter spaces under an additional self-similarity assumption. A simulation study is carried out to illustrate the benefits of utilizing the data from the auxiliary source domains for learning in the target domain.

Locally Adaptive Transfer Learning Algorithms for Large-Scale Multiple Testing

Transfer learning has enjoyed increasing popularity in a range of big data applications. In the context of large-scale multiple testing, the goal is to extract and transfer knowledge learned from related source domains to improve the accuracy of simultaneously testing of a large number of hypotheses in the target domain. This article develops a locally adaptive transfer learning algorithm (LATLA) for transfer learning for multiple testing. In contrast with existing covariate-assisted multiple testing methods that require the auxiliary covariates to be collected alongside the primary data on the same testing units, LATLA provides a principled and generic transfer learning framework that is capable of incorporating multiple samples of auxiliary data from related source domains, possibly in different dimensions/structures and from diverse populations. Both the theoretical and numerical results show that LATLA controls the false discovery rate and outperforms existing methods in power. LATLA is illustrated through an application to genome-wide association studies for the identification of disease-associated SNPs by cross-utilizing the auxiliary data from a related linkage analysis.