Transfer Learning for Contextual Multi-armed Bandits

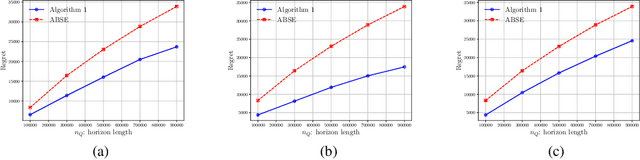
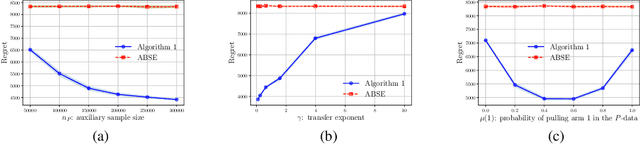
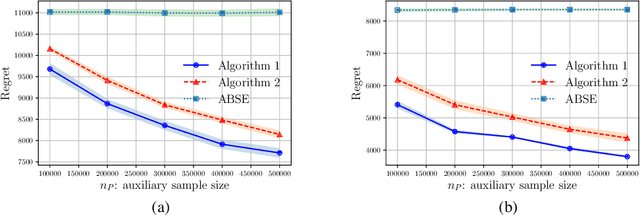
Motivated by a range of applications, we study in this paper the problem of transfer learning for nonparametric contextual multi-armed bandits under the covariate shift model, where we have data collected on source bandits before the start of the target bandit learning. The minimax rate of convergence for the cumulative regret is established and a novel transfer learning algorithm that attains the minimax regret is proposed. The results quantify the contribution of the data from the source domains for learning in the target domain in the context of nonparametric contextual multi-armed bandits. In view of the general impossibility of adaptation to unknown smoothness, we develop a data-driven algorithm that achieves near-optimal statistical guarantees (up to a logarithmic factor) while automatically adapting to the unknown parameters over a large collection of parameter spaces under an additional self-similarity assumption. A simulation study is carried out to illustrate the benefits of utilizing the data from the auxiliary source domains for learning in the target domain.