Are First-Order Diffusion Samplers Really Slower? A Fast Forward-Value Approach

Higher-order ODE solvers have become a standard tool for accelerating diffusion probabilistic model (DPM) sampling, motivating the widespread view that first-order methods are inherently slower and that increasing discretization order is the primary path to faster generation. This paper challenges this belief and revisits acceleration from a complementary angle: beyond solver order, the placement of DPM evaluations along the reverse-time dynamics can substantially affect sampling accuracy in the low-neural function evaluation (NFE) regime. We propose a novel training-free, first-order sampler whose leading discretization error has the opposite sign to that of DDIM. Algorithmically, the method approximates the forward-value evaluation via a cheap one-step lookahead predictor. We provide theoretical guarantees showing that the resulting sampler provably approximates the ideal forward-value trajectory while retaining first-order convergence. Empirically, across standard image generation benchmarks (CIFAR-10, ImageNet, FFHQ, and LSUN), the proposed sampler consistently improves sample quality under the same NFE budget and can be competitive with, and sometimes outperform, state-of-the-art higher-order samplers. Overall, the results suggest that the placement of DPM evaluations provides an additional and largely independent design angle for accelerating diffusion sampling.

A Convergence Theory for Diffusion Language Models: An Information-Theoretic Perspective

Diffusion models have emerged as a powerful paradigm for modern generative modeling, demonstrating strong potential for large language models (LLMs). Unlike conventional autoregressive (AR) models that generate tokens sequentially, diffusion models enable parallel token sampling, leading to faster generation and eliminating left-to-right generation constraints. Despite their empirical success, the theoretical understanding of diffusion model approaches remains underdeveloped. In this work, we develop convergence guarantees for diffusion language models from an information-theoretic perspective. Our analysis demonstrates that the sampling error, measured by the Kullback-Leibler (KL) divergence, decays inversely with the number of iterations $T$ and scales linearly with the mutual information between tokens in the target text sequence. In particular, we establish matching upper and lower bounds, up to some constant factor, to demonstrate the tightness of our convergence analysis. These results offer novel theoretical insights into the practical effectiveness of diffusion language models.

Dimension-Free Convergence of Diffusion Models for Approximate Gaussian Mixtures

Diffusion models are distinguished by their exceptional generative performance, particularly in producing high-quality samples through iterative denoising. While current theory suggests that the number of denoising steps required for accurate sample generation should scale linearly with data dimension, this does not reflect the practical efficiency of widely used algorithms like Denoising Diffusion Probabilistic Models (DDPMs). This paper investigates the effectiveness of diffusion models in sampling from complex high-dimensional distributions that can be well-approximated by Gaussian Mixture Models (GMMs). For these distributions, our main result shows that DDPM takes at most $\widetilde{O}(1/\varepsilon)$ iterations to attain an $\varepsilon$-accurate distribution in total variation (TV) distance, independent of both the ambient dimension $d$ and the number of components $K$, up to logarithmic factors. Furthermore, this result remains robust to score estimation errors. These findings highlight the remarkable effectiveness of diffusion models in high-dimensional settings given the universal approximation capability of GMMs, and provide theoretical insights into their practical success.

Minimax Optimality of the Probability Flow ODE for Diffusion Models

Score-based diffusion models have become a foundational paradigm for modern generative modeling, demonstrating exceptional capability in generating samples from complex high-dimensional distributions. Despite the dominant adoption of probability flow ODE-based samplers in practice due to their superior sampling efficiency and precision, rigorous statistical guarantees for these methods have remained elusive in the literature. This work develops the first end-to-end theoretical framework for deterministic ODE-based samplers that establishes near-minimax optimal guarantees under mild assumptions on target data distributions. Specifically, focusing on subgaussian distributions with $\beta$-H\"older smooth densities for $\beta\leq 2$, we propose a smooth regularized score estimator that simultaneously controls both the $L^2$ score error and the associated mean Jacobian error. Leveraging this estimator within a refined convergence analysis of the ODE-based sampling process, we demonstrate that the resulting sampler achieves the minimax rate in total variation distance, modulo logarithmic factors. Notably, our theory comprehensively accounts for all sources of error in the sampling process and does not require strong structural conditions such as density lower bounds or Lipschitz/smooth scores on target distributions, thereby covering a broad range of practical data distributions.

Provable acceleration for diffusion models under minimal assumptions

While score-based diffusion models have achieved exceptional sampling quality, their sampling speeds are often limited by the high computational burden of score function evaluations. Despite the recent remarkable empirical advances in speeding up the score-based samplers, theoretical understanding of acceleration techniques remains largely limited. To bridge this gap, we propose a novel training-free acceleration scheme for stochastic samplers. Under minimal assumptions -- namely, $L^2$-accurate score estimates and a finite second-moment condition on the target distribution -- our accelerated sampler provably achieves $\varepsilon$-accuracy in total variation within $\widetilde{O}(d^{5/4}/\sqrt{\varepsilon})$ iterations, thereby significantly improving upon the $\widetilde{O}(d/\varepsilon)$ iteration complexity of standard score-based samplers. Notably, our convergence theory does not rely on restrictive assumptions on the target distribution or higher-order score estimation guarantees.

Minimax-optimal trust-aware multi-armed bandits

Multi-armed bandit (MAB) algorithms have achieved significant success in sequential decision-making applications, under the premise that humans perfectly implement the recommended policy. However, existing methods often overlook the crucial factor of human trust in learning algorithms. When trust is lacking, humans may deviate from the recommended policy, leading to undesired learning performance. Motivated by this gap, we study the trust-aware MAB problem by integrating a dynamic trust model into the standard MAB framework. Specifically, it assumes that the recommended and actually implemented policy differs depending on human trust, which in turn evolves with the quality of the recommended policy. We establish the minimax regret in the presence of the trust issue and demonstrate the suboptimality of vanilla MAB algorithms such as the upper confidence bound (UCB) algorithm. To overcome this limitation, we introduce a novel two-stage trust-aware procedure that provably attains near-optimal statistical guarantees. A simulation study is conducted to illustrate the benefits of our proposed algorithm when dealing with the trust issue.

Transfer Learning for Contextual Multi-armed Bandits

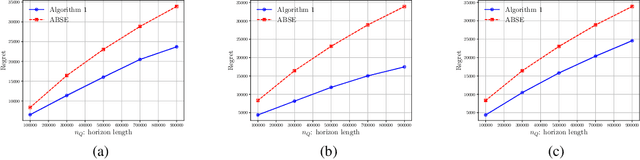
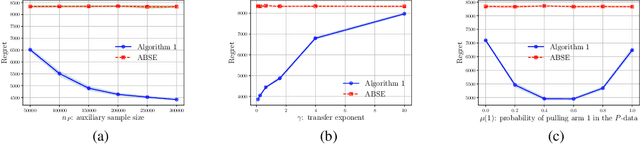
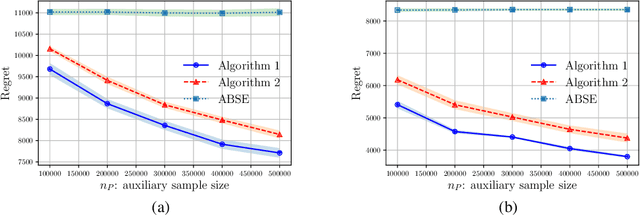
Motivated by a range of applications, we study in this paper the problem of transfer learning for nonparametric contextual multi-armed bandits under the covariate shift model, where we have data collected on source bandits before the start of the target bandit learning. The minimax rate of convergence for the cumulative regret is established and a novel transfer learning algorithm that attains the minimax regret is proposed. The results quantify the contribution of the data from the source domains for learning in the target domain in the context of nonparametric contextual multi-armed bandits. In view of the general impossibility of adaptation to unknown smoothness, we develop a data-driven algorithm that achieves near-optimal statistical guarantees (up to a logarithmic factor) while automatically adapting to the unknown parameters over a large collection of parameter spaces under an additional self-similarity assumption. A simulation study is carried out to illustrate the benefits of utilizing the data from the auxiliary source domains for learning in the target domain.

Minimax Estimation of Linear Functions of Eigenvectors in the Face of Small Eigen-Gaps

Eigenvector perturbation analysis plays a vital role in various statistical data science applications. A large body of prior works, however, focused on establishing $\ell_{2}$ eigenvector perturbation bounds, which are often highly inadequate in addressing tasks that rely on fine-grained behavior of an eigenvector. This paper makes progress on this by studying the perturbation of linear functions of an unknown eigenvector. Focusing on two fundamental problems -- matrix denoising and principal component analysis -- in the presence of Gaussian noise, we develop a suite of statistical theory that characterizes the perturbation of arbitrary linear functions of an unknown eigenvector. In order to mitigate a non-negligible bias issue inherent to the natural "plug-in" estimator, we develop de-biased estimators that (1) achieve minimax lower bounds for a family of scenarios (modulo some logarithmic factor), and (2) can be computed in a data-driven manner without sample splitting. Noteworthily, the proposed estimators are nearly minimax optimal even when the associated eigen-gap is substantially smaller than what is required in prior theory.

Is Q-Learning Minimax Optimal? A Tight Sample Complexity Analysis

Q-learning, which seeks to learn the optimal Q-function of a Markov decision process (MDP) in a model-free fashion, lies at the heart of reinforcement learning. When it comes to the synchronous setting (such that independent samples for all state-action pairs are drawn from a generative model in each iteration), substantial progress has been made recently towards understanding the sample efficiency of Q-learning. Take a $\gamma$-discounted infinite-horizon MDP with state space $\mathcal{S}$ and action space $\mathcal{A}$: to yield an entrywise $\varepsilon$-accurate estimate of the optimal Q-function, state-of-the-art theory for Q-learning proves that a sample size on the order of $\frac{|\mathcal{S}||\mathcal{A}|}{(1-\gamma)^5\varepsilon^{2}}$ is sufficient, which, however, fails to match with the existing minimax lower bound. This gives rise to natural questions: what is the sharp sample complexity of Q-learning? Is Q-learning provably sub-optimal? In this work, we settle these questions by (1) demonstrating that the sample complexity of Q-learning is at most on the order of $\frac{|\mathcal{S}||\mathcal{A}|}{(1-\gamma)^4\varepsilon^2}$ (up to some log factor) for any $0<\varepsilon <1$, and (2) developing a matching lower bound to confirm the sharpness of our result. Our findings unveil both the effectiveness and limitation of Q-learning: its sample complexity matches that of speedy Q-learning without requiring extra computation and storage, albeit still being considerably higher than the minimax lower bound.

Uncertainty quantification for nonconvex tensor completion: Confidence intervals, heteroscedasticity and optimality

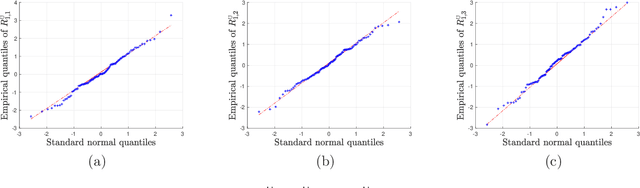
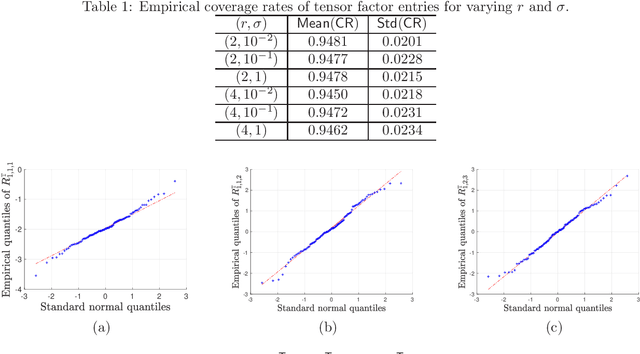
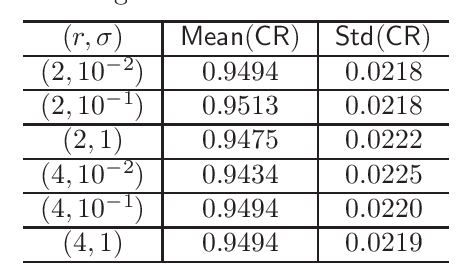
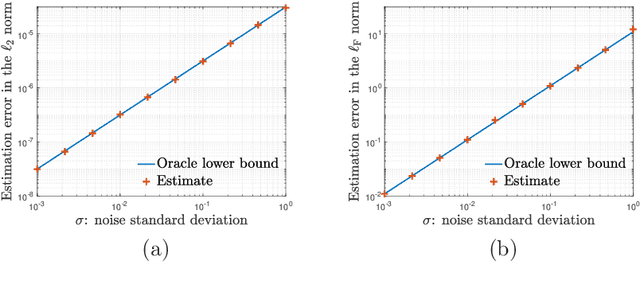
We study the distribution and uncertainty of nonconvex optimization for noisy tensor completion -- the problem of estimating a low-rank tensor given incomplete and corrupted observations of its entries. Focusing on a two-stage estimation algorithm proposed by Cai et al. (2019), we characterize the distribution of this nonconvex estimator down to fine scales. This distributional theory in turn allows one to construct valid and short confidence intervals for both the unseen tensor entries and the unknown tensor factors. The proposed inferential procedure enjoys several important features: (1) it is fully adaptive to noise heteroscedasticity, and (2) it is data-driven and automatically adapts to unknown noise distributions. Furthermore, our findings unveil the statistical optimality of nonconvex tensor completion: it attains un-improvable $\ell_{2}$ accuracy -- including both the rates and the pre-constants -- when estimating both the unknown tensor and the underlying tensor factors.