Gen Li
Towards Efficient Online Exploration for Reinforcement Learning with Human Feedback
Sep 26, 2025Abstract:Reinforcement learning with human feedback (RLHF), which learns a reward model from human preference data and then optimizes a policy to favor preferred responses, has emerged as a central paradigm for aligning large language models (LLMs) with human preferences. In this paper, we investigate exploration principles for online RLHF, where one seeks to adaptively collect new preference data to refine both the reward model and the policy in a data-efficient manner. By examining existing optimism-based exploration algorithms, we identify a drawback in their sampling protocol: they tend to gather comparisons that fail to reduce the most informative uncertainties in reward differences, and we prove lower bounds showing that such methods can incur linear regret over exponentially long horizons. Motivated by this insight, we propose a new exploration scheme that directs preference queries toward reducing uncertainty in reward differences most relevant to policy improvement. Under a multi-armed bandit model of RLHF, we establish regret bounds of order $T^{(\beta+1)/(\beta+2)}$, where $\beta>0$ is a hyperparameter that balances reward maximization against mitigating distribution shift. To our knowledge, this is the first online RLHF algorithm with regret scaling polynomially in all model parameters.
HuMo: Human-Centric Video Generation via Collaborative Multi-Modal Conditioning
Sep 10, 2025Abstract:Human-Centric Video Generation (HCVG) methods seek to synthesize human videos from multimodal inputs, including text, image, and audio. Existing methods struggle to effectively coordinate these heterogeneous modalities due to two challenges: the scarcity of training data with paired triplet conditions and the difficulty of collaborating the sub-tasks of subject preservation and audio-visual sync with multimodal inputs. In this work, we present HuMo, a unified HCVG framework for collaborative multimodal control. For the first challenge, we construct a high-quality dataset with diverse and paired text, reference images, and audio. For the second challenge, we propose a two-stage progressive multimodal training paradigm with task-specific strategies. For the subject preservation task, to maintain the prompt following and visual generation abilities of the foundation model, we adopt the minimal-invasive image injection strategy. For the audio-visual sync task, besides the commonly adopted audio cross-attention layer, we propose a focus-by-predicting strategy that implicitly guides the model to associate audio with facial regions. For joint learning of controllabilities across multimodal inputs, building on previously acquired capabilities, we progressively incorporate the audio-visual sync task. During inference, for flexible and fine-grained multimodal control, we design a time-adaptive Classifier-Free Guidance strategy that dynamically adjusts guidance weights across denoising steps. Extensive experimental results demonstrate that HuMo surpasses specialized state-of-the-art methods in sub-tasks, establishing a unified framework for collaborative multimodal-conditioned HCVG. Project Page: https://phantom-video.github.io/HuMo.
Connections between reinforcement learning with feedback,test-time scaling, and diffusion guidance: An anthology
Sep 04, 2025Abstract:In this note, we reflect on several fundamental connections among widely used post-training techniques. We clarify some intimate connections and equivalences between reinforcement learning with human feedback, reinforcement learning with internal feedback, and test-time scaling (particularly soft best-of-$N$ sampling), while also illuminating intrinsic links between diffusion guidance and test-time scaling. Additionally, we introduce a resampling approach for alignment and reward-directed diffusion models, sidestepping the need for explicit reinforcement learning techniques.
Can Structured Templates Facilitate LLMs in Tackling Harder Tasks? : An Exploration of Scaling Laws by Difficulty
Aug 26, 2025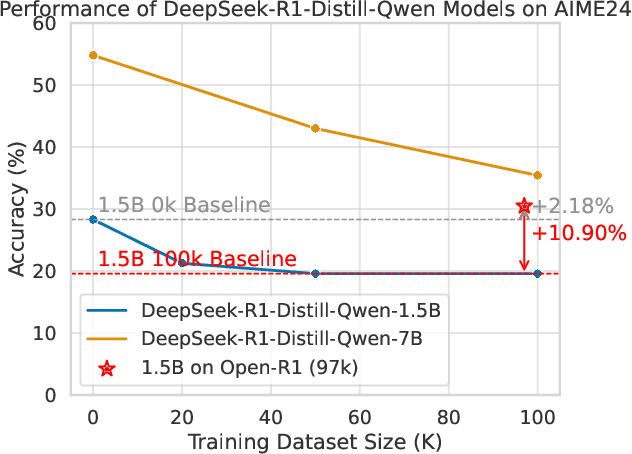
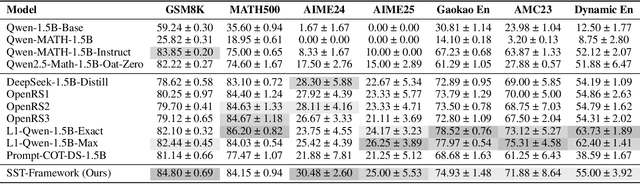
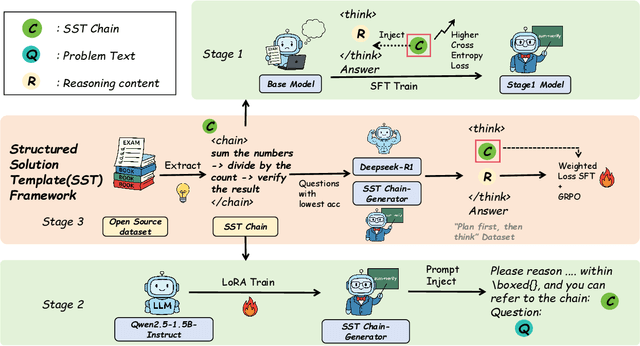

Abstract:Structured, procedural reasoning is essential for Large Language Models (LLMs), especially in mathematics. While post-training methods have improved LLM performance, they still fall short in capturing deep procedural logic on complex tasks. To tackle the issue, in this paper, we first investigate this limitation and uncover a novel finding: a Scaling Law by Difficulty, which reveals that model performance follows a U-shaped curve with respect to training data complexity -- excessive low-difficulty data impedes abstraction, while high-difficulty data significantly enhances reasoning ability. Motivated by this, we propose the Structured Solution Template (SST) framework, which uses solution templates and a curriculum of varied difficulty to explicitly teach procedural reasoning. Specifically, SST comprises (1) fine-tuning with structured solution-template chains and dynamically weighted loss to prioritize procedural logic, (2) prompt-time injection of solution templates as cognitive scaffolds to guide inference, and (3) integrated curriculum fine-tuning that explicitly teaches the model to self-plan - execute - self-correct. Experiments on GSM8K, AIME24, and new Dynamic En benchmark show that SST significantly improves both accuracy and efficiency, especially on harder problems.
Dual Enhancement on 3D Vision-Language Perception for Monocular 3D Visual Grounding
Aug 26, 2025Abstract:Monocular 3D visual grounding is a novel task that aims to locate 3D objects in RGB images using text descriptions with explicit geometry information. Despite the inclusion of geometry details in the text, we observe that the text embeddings are sensitive to the magnitude of numerical values but largely ignore the associated measurement units. For example, simply equidistant mapping the length with unit "meter" to "decimeters" or "centimeters" leads to severe performance degradation, even though the physical length remains equivalent. This observation signifies the weak 3D comprehension of pre-trained language model, which generates misguiding text features to hinder 3D perception. Therefore, we propose to enhance the 3D perception of model on text embeddings and geometry features with two simple and effective methods. Firstly, we introduce a pre-processing method named 3D-text Enhancement (3DTE), which enhances the comprehension of mapping relationships between different units by augmenting the diversity of distance descriptors in text queries. Next, we propose a Text-Guided Geometry Enhancement (TGE) module to further enhance the 3D-text information by projecting the basic text features into geometrically consistent space. These 3D-enhanced text features are then leveraged to precisely guide the attention of geometry features. We evaluate the proposed method through extensive comparisons and ablation studies on the Mono3DRefer dataset. Experimental results demonstrate substantial improvements over previous methods, achieving new state-of-the-art results with a notable accuracy gain of 11.94\% in the "Far" scenario. Our code will be made publicly available.
Hydra-Bench: A Benchmark for Multi-Modal Leaf Wetness Sensing
Jul 30, 2025Abstract:Leaf wetness detection is a crucial task in agricultural monitoring, as it directly impacts the prediction and protection of plant diseases. However, existing sensing systems suffer from limitations in robustness, accuracy, and environmental resilience when applied to natural leaves under dynamic real-world conditions. To address these challenges, we introduce a new multi-modal dataset specifically designed for evaluating and advancing machine learning algorithms in leaf wetness detection. Our dataset comprises synchronized mmWave raw data, Synthetic Aperture Radar (SAR) images, and RGB images collected over six months from five diverse plant species in both controlled and outdoor field environments. We provide detailed benchmarks using the Hydra model, including comparisons against single modality baselines and multiple fusion strategies, as well as performance under varying scan distances. Additionally, our dataset can serve as a benchmark for future SAR imaging algorithm optimization, enabling a systematic evaluation of detection accuracy under diverse conditions.
Phantom-Data : Towards a General Subject-Consistent Video Generation Dataset
Jun 23, 2025Abstract:Subject-to-video generation has witnessed substantial progress in recent years. However, existing models still face significant challenges in faithfully following textual instructions. This limitation, commonly known as the copy-paste problem, arises from the widely used in-pair training paradigm. This approach inherently entangles subject identity with background and contextual attributes by sampling reference images from the same scene as the target video. To address this issue, we introduce \textbf{Phantom-Data, the first general-purpose cross-pair subject-to-video consistency dataset}, containing approximately one million identity-consistent pairs across diverse categories. Our dataset is constructed via a three-stage pipeline: (1) a general and input-aligned subject detection module, (2) large-scale cross-context subject retrieval from more than 53 million videos and 3 billion images, and (3) prior-guided identity verification to ensure visual consistency under contextual variation. Comprehensive experiments show that training with Phantom-Data significantly improves prompt alignment and visual quality while preserving identity consistency on par with in-pair baselines.
EgoM2P: Egocentric Multimodal Multitask Pretraining
Jun 09, 2025Abstract:Understanding multimodal signals in egocentric vision, such as RGB video, depth, camera poses, and gaze, is essential for applications in augmented reality, robotics, and human-computer interaction. These capabilities enable systems to better interpret the camera wearer's actions, intentions, and surrounding environment. However, building large-scale egocentric multimodal and multitask models presents unique challenges. Egocentric data are inherently heterogeneous, with large variations in modality coverage across devices and settings. Generating pseudo-labels for missing modalities, such as gaze or head-mounted camera trajectories, is often infeasible, making standard supervised learning approaches difficult to scale. Furthermore, dynamic camera motion and the complex temporal and spatial structure of first-person video pose additional challenges for the direct application of existing multimodal foundation models. To address these challenges, we introduce a set of efficient temporal tokenizers and propose EgoM2P, a masked modeling framework that learns from temporally aware multimodal tokens to train a large, general-purpose model for egocentric 4D understanding. This unified design supports multitasking across diverse egocentric perception and synthesis tasks, including gaze prediction, egocentric camera tracking, and monocular depth estimation from egocentric video. EgoM2P also serves as a generative model for conditional egocentric video synthesis. Across these tasks, EgoM2P matches or outperforms specialist models while being an order of magnitude faster. We will fully open-source EgoM2P to support the community and advance egocentric vision research. Project page: https://egom2p.github.io/
Transformers Meet In-Context Learning: A Universal Approximation Theory
Jun 05, 2025Abstract:Modern large language models are capable of in-context learning, the ability to perform new tasks at inference time using only a handful of input-output examples in the prompt, without any fine-tuning or parameter updates. We develop a universal approximation theory to better understand how transformers enable in-context learning. For any class of functions (each representing a distinct task), we demonstrate how to construct a transformer that, without any further weight updates, can perform reliable prediction given only a few in-context examples. In contrast to much of the recent literature that frames transformers as algorithm approximators -- i.e., constructing transformers to emulate the iterations of optimization algorithms as a means to approximate solutions of learning problems -- our work adopts a fundamentally different approach rooted in universal function approximation. This alternative approach offers approximation guarantees that are not constrained by the effectiveness of the optimization algorithms being approximated, thereby extending far beyond convex problems and linear function classes. Our construction sheds light on how transformers can simultaneously learn general-purpose representations and adapt dynamically to in-context examples.
A Convergence Theory for Diffusion Language Models: An Information-Theoretic Perspective
May 27, 2025Abstract:Diffusion models have emerged as a powerful paradigm for modern generative modeling, demonstrating strong potential for large language models (LLMs). Unlike conventional autoregressive (AR) models that generate tokens sequentially, diffusion models enable parallel token sampling, leading to faster generation and eliminating left-to-right generation constraints. Despite their empirical success, the theoretical understanding of diffusion model approaches remains underdeveloped. In this work, we develop convergence guarantees for diffusion language models from an information-theoretic perspective. Our analysis demonstrates that the sampling error, measured by the Kullback-Leibler (KL) divergence, decays inversely with the number of iterations $T$ and scales linearly with the mutual information between tokens in the target text sequence. In particular, we establish matching upper and lower bounds, up to some constant factor, to demonstrate the tightness of our convergence analysis. These results offer novel theoretical insights into the practical effectiveness of diffusion language models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge