Adaptivity and Convergence of Probability Flow ODEs in Diffusion Generative Models

Score-based generative models, which transform noise into data by learning to reverse a diffusion process, have become a cornerstone of modern generative AI. This paper contributes to establishing theoretical guarantees for the probability flow ODE, a widely used diffusion-based sampler known for its practical efficiency. While a number of prior works address its general convergence theory, it remains unclear whether the probability flow ODE sampler can adapt to the low-dimensional structures commonly present in natural image data. We demonstrate that, with accurate score function estimation, the probability flow ODE sampler achieves a convergence rate of $O(k/T)$ in total variation distance (ignoring logarithmic factors), where $k$ is the intrinsic dimension of the target distribution and $T$ is the number of iterations. This dimension-free convergence rate improves upon existing results that scale with the typically much larger ambient dimension, highlighting the ability of the probability flow ODE sampler to exploit intrinsic low-dimensional structures in the target distribution for faster sampling.

$O(d/T)$ Convergence Theory for Diffusion Probabilistic Models under Minimal Assumptions

Score-based diffusion models, which generate new data by learning to reverse a diffusion process that perturbs data from the target distribution into noise, have achieved remarkable success across various generative tasks. Despite their superior empirical performance, existing theoretical guarantees are often constrained by stringent assumptions or suboptimal convergence rates. In this paper, we establish a fast convergence theory for a popular SDE-based sampler under minimal assumptions. Our analysis shows that, provided $\ell_{2}$-accurate estimates of the score functions, the total variation distance between the target and generated distributions is upper bounded by $O(d/T)$ (ignoring logarithmic factors), where $d$ is the data dimensionality and $T$ is the number of steps. This result holds for any target distribution with finite first-order moment. To our knowledge, this improves upon existing convergence theory for both the SDE-based sampler and another ODE-based sampler, while imposing minimal assumptions on the target data distribution and score estimates. This is achieved through a novel set of analytical tools that provides a fine-grained characterization of how the error propagates at each step of the reverse process.

A Score-Based Density Formula, with Applications in Diffusion Generative Models

Score-based generative models (SGMs) have revolutionized the field of generative modeling, achieving unprecedented success in generating realistic and diverse content. Despite empirical advances, the theoretical basis for why optimizing the evidence lower bound (ELBO) on the log-likelihood is effective for training diffusion generative models, such as DDPMs, remains largely unexplored. In this paper, we address this question by establishing a density formula for a continuous-time diffusion process, which can be viewed as the continuous-time limit of the forward process in an SGM. This formula reveals the connection between the target density and the score function associated with each step of the forward process. Building on this, we demonstrate that the minimizer of the optimization objective for training DDPMs nearly coincides with that of the true objective, providing a theoretical foundation for optimizing DDPMs using the ELBO. Furthermore, we offer new insights into the role of score-matching regularization in training GANs, the use of ELBO in diffusion classifiers, and the recently proposed diffusion loss.

Analysis of the ICML 2023 Ranking Data: Can Authors' Opinions of Their Own Papers Assist Peer Review in Machine Learning?

We conducted an experiment during the review process of the 2023 International Conference on Machine Learning (ICML) that requested authors with multiple submissions to rank their own papers based on perceived quality. We received 1,342 rankings, each from a distinct author, pertaining to 2,592 submissions. In this paper, we present an empirical analysis of how author-provided rankings could be leveraged to improve peer review processes at machine learning conferences. We focus on the Isotonic Mechanism, which calibrates raw review scores using author-provided rankings. Our analysis demonstrates that the ranking-calibrated scores outperform raw scores in estimating the ground truth ``expected review scores'' in both squared and absolute error metrics. Moreover, we propose several cautious, low-risk approaches to using the Isotonic Mechanism and author-provided rankings in peer review processes, including assisting senior area chairs' oversight of area chairs' recommendations, supporting the selection of paper awards, and guiding the recruitment of emergency reviewers. We conclude the paper by addressing the study's limitations and proposing future research directions.

When can weak latent factors be statistically inferred?

This article establishes a new and comprehensive estimation and inference theory for principal component analysis (PCA) under the weak factor model that allow for cross-sectional dependent idiosyncratic components under nearly minimal the factor strength relative to the noise level or signal-to-noise ratio. Our theory is applicable regardless of the relative growth rate between the cross-sectional dimension $N$ and temporal dimension $T$. This more realistic assumption and noticeable result requires completely new technical device, as the commonly-used leave-one-out trick is no longer applicable to the case with cross-sectional dependence. Another notable advancement of our theory is on PCA inference $ - $ for example, under the regime where $N\asymp T$, we show that the asymptotic normality for the PCA-based estimator holds as long as the signal-to-noise ratio (SNR) grows faster than a polynomial rate of $\log N$. This finding significantly surpasses prior work that required a polynomial rate of $N$. Our theory is entirely non-asymptotic, offering finite-sample characterizations for both the estimation error and the uncertainty level of statistical inference. A notable technical innovation is our closed-form first-order approximation of PCA-based estimator, which paves the way for various statistical tests. Furthermore, we apply our theories to design easy-to-implement statistics for validating whether given factors fall in the linear spans of unknown latent factors, testing structural breaks in the factor loadings for an individual unit, checking whether two units have the same risk exposures, and constructing confidence intervals for systematic risks. Our empirical studies uncover insightful correlations between our test results and economic cycles.

Adapting to Unknown Low-Dimensional Structures in Score-Based Diffusion Models

This paper investigates score-based diffusion models when the underlying target distribution is concentrated on or near low-dimensional manifolds within the higher-dimensional space in which they formally reside, a common characteristic of natural image distributions. Despite previous efforts to understand the data generation process of diffusion models, existing theoretical support remains highly suboptimal in the presence of low-dimensional structure, which we strengthen in this paper. For the popular Denoising Diffusion Probabilistic Model (DDPM), we find that the dependency of the error incurred within each denoising step on the ambient dimension $d$ is in general unavoidable. We further identify a unique design of coefficients that yields a converges rate at the order of $O(k^{2}/\sqrt{T})$ (up to log factors), where $k$ is the intrinsic dimension of the target distribution and $T$ is the number of steps. This represents the first theoretical demonstration that the DDPM sampler can adapt to unknown low-dimensional structures in the target distribution, highlighting the critical importance of coefficient design. All of this is achieved by a novel set of analysis tools that characterize the algorithmic dynamics in a more deterministic manner.

Enhancing AI Diagnostics: Autonomous Lesion Masking via Semi-Supervised Deep Learning

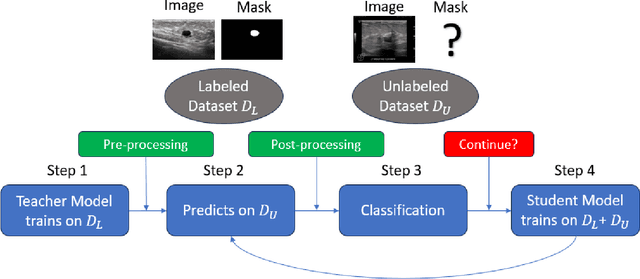
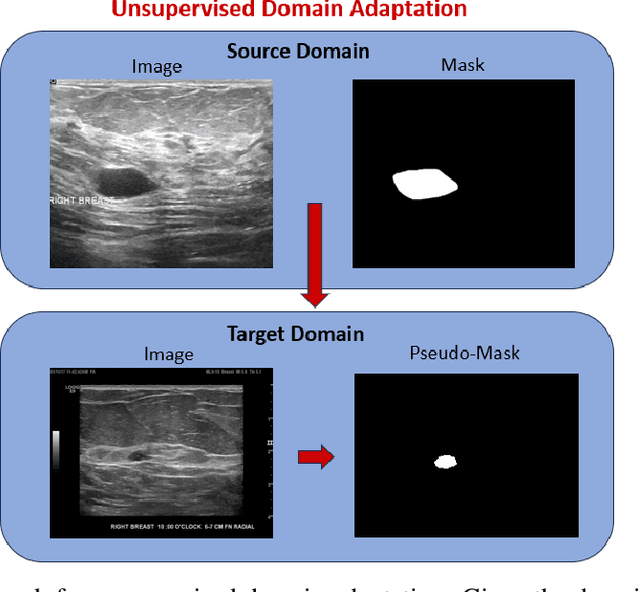
This study presents an unsupervised domain adaptation method aimed at autonomously generating image masks outlining regions of interest (ROIs) for differentiating breast lesions in breast ultrasound (US) imaging. Our semi-supervised learning approach utilizes a primitive model trained on a small public breast US dataset with true annotations. This model is then iteratively refined for the domain adaptation task, generating pseudo-masks for our private, unannotated breast US dataset. The dataset, twice the size of the public one, exhibits considerable variability in image acquisition perspectives and demographic representation, posing a domain-shift challenge. Unlike typical domain adversarial training, we employ downstream classification outcomes as a benchmark to guide the updating of pseudo-masks in subsequent iterations. We found the classification precision to be highly correlated with the completeness of the generated ROIs, which promotes the explainability of the deep learning classification model. Preliminary findings demonstrate the efficacy and reliability of this approach in streamlining the ROI annotation process, thereby enhancing the classification and localization of breast lesions for more precise and interpretable diagnoses.

Entrywise Inference for Causal Panel Data: A Simple and Instance-Optimal Approach

In causal inference with panel data under staggered adoption, the goal is to estimate and derive confidence intervals for potential outcomes and treatment effects. We propose a computationally efficient procedure, involving only simple matrix algebra and singular value decomposition. We derive non-asymptotic bounds on the entrywise error, establishing its proximity to a suitably scaled Gaussian variable. Despite its simplicity, our procedure turns out to be instance-optimal, in that our theoretical scaling matches a local instance-wise lower bound derived via a Bayesian Cram\'{e}r-Rao argument. Using our insights, we develop a data-driven procedure for constructing entrywise confidence intervals with pre-specified coverage guarantees. Our analysis is based on a general inferential toolbox for the SVD algorithm applied to the matrix denoising model, which might be of independent interest.

The Isotonic Mechanism for Exponential Family Estimation

In 2023, the International Conference on Machine Learning (ICML) required authors with multiple submissions to rank their submissions based on perceived quality. In this paper, we aim to employ these author-specified rankings to enhance peer review in machine learning and artificial intelligence conferences by extending the Isotonic Mechanism (Su, 2021, 2022) to exponential family distributions. This mechanism generates adjusted scores closely align with the original scores while adhering to author-specified rankings. Despite its applicability to a broad spectrum of exponential family distributions, this mechanism's implementation does not necessitate knowledge of the specific distribution form. We demonstrate that an author is incentivized to provide accurate rankings when her utility takes the form of a convex additive function of the adjusted review scores. For a certain subclass of exponential family distributions, we prove that the author reports truthfully only if the question involves only pairwise comparisons between her submissions, thus indicating the optimality of ranking in truthful information elicitation. Lastly, we show that the adjusted scores improve dramatically the accuracy of the original scores and achieve nearly minimax optimality for estimating the true scores with statistical consistecy when true scores have bounded total variation.

Minimax-Optimal Reward-Agnostic Exploration in Reinforcement Learning

This paper studies reward-agnostic exploration in reinforcement learning (RL) -- a scenario where the learner is unware of the reward functions during the exploration stage -- and designs an algorithm that improves over the state of the art. More precisely, consider a finite-horizon non-stationary Markov decision process with $S$ states, $A$ actions, and horizon length $H$, and suppose that there are no more than a polynomial number of given reward functions of interest. By collecting an order of \begin{align*} \frac{SAH^3}{\varepsilon^2} \text{ sample episodes (up to log factor)} \end{align*} without guidance of the reward information, our algorithm is able to find $\varepsilon$-optimal policies for all these reward functions, provided that $\varepsilon$ is sufficiently small. This forms the first reward-agnostic exploration scheme in this context that achieves provable minimax optimality. Furthermore, once the sample size exceeds $\frac{S^2AH^3}{\varepsilon^2}$ episodes (up to log factor), our algorithm is able to yield $\varepsilon$ accuracy for arbitrarily many reward functions (even when they are adversarially designed), a task commonly dubbed as ``reward-free exploration.'' The novelty of our algorithm design draws on insights from offline RL: the exploration scheme attempts to maximize a critical reward-agnostic quantity that dictates the performance of offline RL, while the policy learning paradigm leverages ideas from sample-optimal offline RL paradigms.