Uncertainty quantification for nonconvex tensor completion: Confidence intervals, heteroscedasticity and optimality
Paper and Code
Jun 15, 2020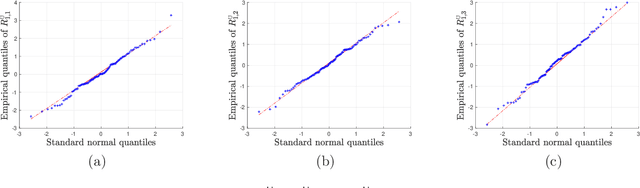
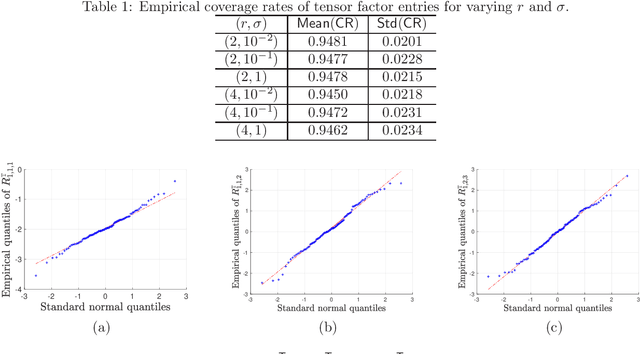
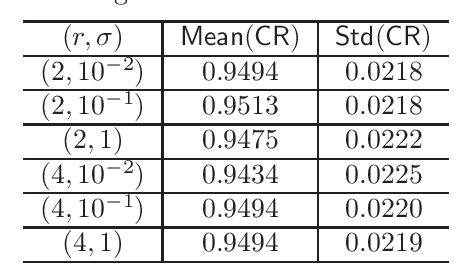
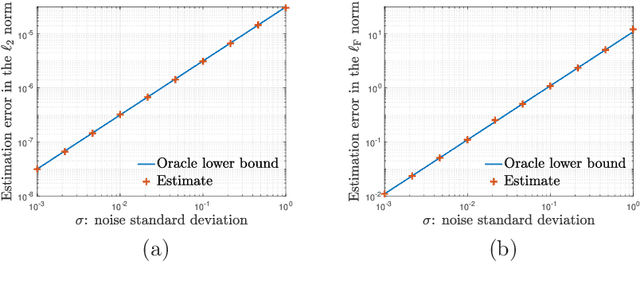
We study the distribution and uncertainty of nonconvex optimization for noisy tensor completion -- the problem of estimating a low-rank tensor given incomplete and corrupted observations of its entries. Focusing on a two-stage estimation algorithm proposed by Cai et al. (2019), we characterize the distribution of this nonconvex estimator down to fine scales. This distributional theory in turn allows one to construct valid and short confidence intervals for both the unseen tensor entries and the unknown tensor factors. The proposed inferential procedure enjoys several important features: (1) it is fully adaptive to noise heteroscedasticity, and (2) it is data-driven and automatically adapts to unknown noise distributions. Furthermore, our findings unveil the statistical optimality of nonconvex tensor completion: it attains un-improvable $\ell_{2}$ accuracy -- including both the rates and the pre-constants -- when estimating both the unknown tensor and the underlying tensor factors.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge