Stage-wise Dynamics of Classifier-Free Guidance in Diffusion Models

Classifier-Free Guidance (CFG) is widely used to improve conditional fidelity in diffusion models, but its impact on sampling dynamics remains poorly understood. Prior studies, often restricted to unimodal conditional distributions or simplified cases, provide only a partial picture. We analyze CFG under multimodal conditionals and show that the sampling process unfolds in three successive stages. In the Direction Shift stage, guidance accelerates movement toward the weighted mean, introducing initialization bias and norm growth. In the Mode Separation stage, local dynamics remain largely neutral, but the inherited bias suppresses weaker modes, reducing global diversity. In the Concentration stage, guidance amplifies within-mode contraction, diminishing fine-grained variability. This unified view explains a widely observed phenomenon: stronger guidance improves semantic alignment but inevitably reduces diversity. Experiments support these predictions, showing that early strong guidance erodes global diversity, while late strong guidance suppresses fine-grained variation. Moreover, our theory naturally suggests a time-varying guidance schedule, and empirical results confirm that it consistently improves both quality and diversity.

ReTrack: Data Unlearning in Diffusion Models through Redirecting the Denoising Trajectory

Diffusion models excel at generating high-quality, diverse images but suffer from training data memorization, raising critical privacy and safety concerns. Data unlearning has emerged to mitigate this issue by removing the influence of specific data without retraining from scratch. We propose ReTrack, a fast and effective data unlearning method for diffusion models. ReTrack employs importance sampling to construct a more efficient fine-tuning loss, which we approximate by retaining only dominant terms. This yields an interpretable objective that redirects denoising trajectories toward the $k$-nearest neighbors, enabling efficient unlearning while preserving generative quality. Experiments on MNIST T-Shirt, CelebA-HQ, CIFAR-10, and Stable Diffusion show that ReTrack achieves state-of-the-art performance, striking the best trade-off between unlearning strength and generation quality preservation.

M$^2$CD: A Unified MultiModal Framework for Optical-SAR Change Detection with Mixture of Experts and Self-Distillation

Most existing change detection (CD) methods focus on optical images captured at different times, and deep learning (DL) has achieved remarkable success in this domain. However, in extreme scenarios such as disaster response, synthetic aperture radar (SAR), with its active imaging capability, is more suitable for providing post-event data. This introduces new challenges for CD methods, as existing weight-sharing Siamese networks struggle to effectively learn the cross-modal data distribution between optical and SAR images. To address this challenge, we propose a unified MultiModal CD framework, M$^2$CD. We integrate Mixture of Experts (MoE) modules into the backbone to explicitly handle diverse modalities, thereby enhancing the model's ability to learn multimodal data distributions. Additionally, we innovatively propose an Optical-to-SAR guided path (O2SP) and implement self-distillation during training to reduce the feature space discrepancy between different modalities, further alleviating the model's learning burden. We design multiple variants of M$^2$CD based on both CNN and Transformer backbones. Extensive experiments validate the effectiveness of the proposed framework, with the MiT-b1 version of M$^2$CD outperforming all state-of-the-art (SOTA) methods in optical-SAR CD tasks.

Improving Diffusion-based Inverse Algorithms under Few-Step Constraint via Learnable Linear Extrapolation

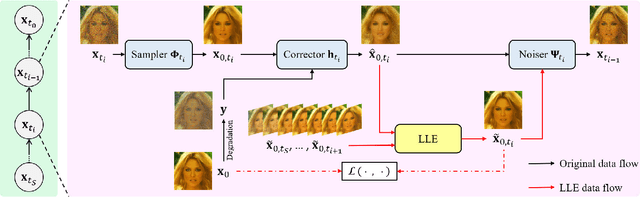
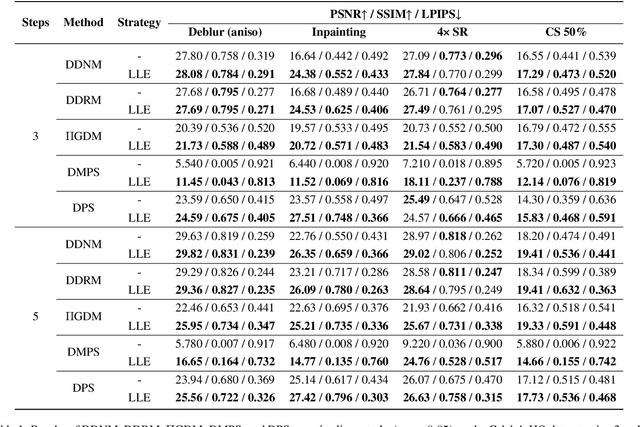
Diffusion models have demonstrated remarkable performance in modeling complex data priors, catalyzing their widespread adoption in solving various inverse problems. However, the inherently iterative nature of diffusion-based inverse algorithms often requires hundreds to thousands of steps, with performance degradation occurring under fewer steps which limits their practical applicability. While high-order diffusion ODE solvers have been extensively explored for efficient diffusion sampling without observations, their application to inverse problems remains underexplored due to the diverse forms of inverse algorithms and their need for repeated trajectory correction based on observations. To address this gap, we first introduce a canonical form that decomposes existing diffusion-based inverse algorithms into three modules to unify their analysis. Inspired by the linear subspace search strategy in the design of high-order diffusion ODE solvers, we propose the Learnable Linear Extrapolation (LLE) method, a lightweight approach that universally enhances the performance of any diffusion-based inverse algorithm that fits the proposed canonical form. Extensive experiments demonstrate consistent improvements of the proposed LLE method across multiple algorithms and tasks, indicating its potential for more efficient solutions and boosted performance of diffusion-based inverse algorithms with limited steps. Codes for reproducing our experiments are available at \href{https://github.com/weigerzan/LLE_inverse_problem}{https://github.com/weigerzan/LLE\_inverse\_problem}.

JL1-CD: A New Benchmark for Remote Sensing Change Detection and a Robust Multi-Teacher Knowledge Distillation Framework

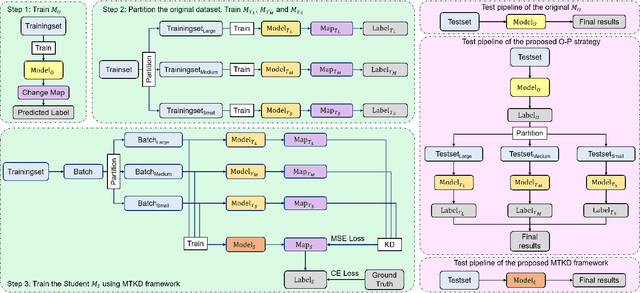
Deep learning has achieved significant success in the field of remote sensing image change detection (CD), yet two major challenges remain: the scarcity of sub-meter, all-inclusive open-source CD datasets, and the difficulty of achieving consistent and satisfactory detection results across images with varying change areas. To address these issues, we introduce the JL1-CD dataset, which contains 5,000 pairs of 512 x 512 pixel images with a resolution of 0.5 to 0.75 meters. Additionally, we propose a multi-teacher knowledge distillation (MTKD) framework for CD. Experimental results on the JL1-CD and SYSU-CD datasets demonstrate that the MTKD framework significantly improves the performance of CD models with various network architectures and parameter sizes, achieving new state-of-the-art results. The code is available at https://github.com/circleLZY/MTKD-CD.

See it, Think it, Sorted: Large Multimodal Models are Few-shot Time Series Anomaly Analyzers

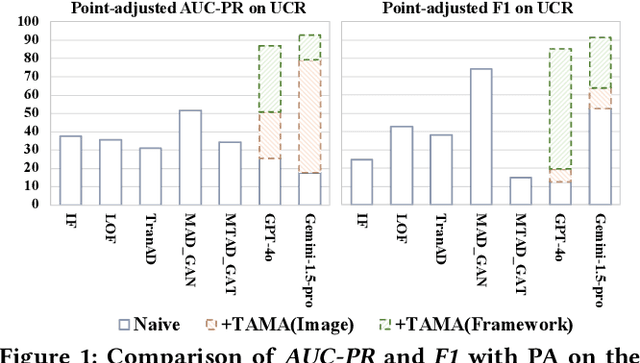
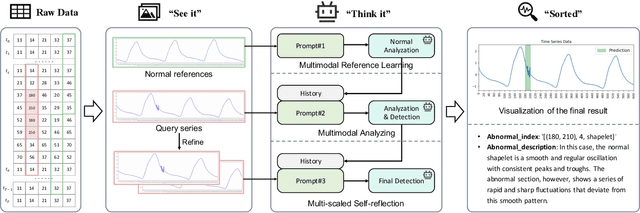
Time series anomaly detection (TSAD) is becoming increasingly vital due to the rapid growth of time series data across various sectors. Anomalies in web service data, for example, can signal critical incidents such as system failures or server malfunctions, necessitating timely detection and response. However, most existing TSAD methodologies rely heavily on manual feature engineering or require extensive labeled training data, while also offering limited interpretability. To address these challenges, we introduce a pioneering framework called the Time Series Anomaly Multimodal Analyzer (TAMA), which leverages the power of Large Multimodal Models (LMMs) to enhance both the detection and interpretation of anomalies in time series data. By converting time series into visual formats that LMMs can efficiently process, TAMA leverages few-shot in-context learning capabilities to reduce dependence on extensive labeled datasets. Our methodology is validated through rigorous experimentation on multiple real-world datasets, where TAMA consistently outperforms state-of-the-art methods in TSAD tasks. Additionally, TAMA provides rich, natural language-based semantic analysis, offering deeper insights into the nature of detected anomalies. Furthermore, we contribute one of the first open-source datasets that includes anomaly detection labels, anomaly type labels, and contextual description, facilitating broader exploration and advancement within this critical field. Ultimately, TAMA not only excels in anomaly detection but also provides a comprehensive approach for understanding the underlying causes of anomalies, pushing TSAD forward through innovative methodologies and insights.

Unleashing the Denoising Capability of Diffusion Prior for Solving Inverse Problems

The recent emergence of diffusion models has significantly advanced the precision of learnable priors, presenting innovative avenues for addressing inverse problems. Since inverse problems inherently entail maximum a posteriori estimation, previous works have endeavored to integrate diffusion priors into the optimization frameworks. However, prevailing optimization-based inverse algorithms primarily exploit the prior information within the diffusion models while neglecting their denoising capability. To bridge this gap, this work leverages the diffusion process to reframe noisy inverse problems as a two-variable constrained optimization task by introducing an auxiliary optimization variable. By employing gradient truncation, the projection gradient descent method is efficiently utilized to solve the corresponding optimization problem. The proposed algorithm, termed ProjDiff, effectively harnesses the prior information and the denoising capability of a pre-trained diffusion model within the optimization framework. Extensive experiments on the image restoration tasks and source separation and partial generation tasks demonstrate that ProjDiff exhibits superior performance across various linear and nonlinear inverse problems, highlighting its potential for practical applications. Code is available at https://github.com/weigerzan/ProjDiff/.

EPA: Neural Collapse Inspired Robust Out-of-Distribution Detector

Out-of-distribution (OOD) detection plays a crucial role in ensuring the security of neural networks. Existing works have leveraged the fact that In-distribution (ID) samples form a subspace in the feature space, achieving state-of-the-art (SOTA) performance. However, the comprehensive characteristics of the ID subspace still leave under-explored. Recently, the discovery of Neural Collapse ($\mathcal{NC}$) sheds light on novel properties of the ID subspace. Leveraging insight from $\mathcal{NC}$, we observe that the Principal Angle between the features and the ID feature subspace forms a superior representation for measuring the likelihood of OOD. Building upon this observation, we propose a novel $\mathcal{NC}$-inspired OOD scoring function, named Entropy-enhanced Principal Angle (EPA), which integrates both the global characteristic of the ID subspace and its inner property. We experimentally compare EPA with various SOTA approaches, validating its superior performance and robustness across different network architectures and OOD datasets.

Unravel Anomalies: An End-to-end Seasonal-Trend Decomposition Approach for Time Series Anomaly Detection

Traditional Time-series Anomaly Detection (TAD) methods often struggle with the composite nature of complex time-series data and a diverse array of anomalies. We introduce TADNet, an end-to-end TAD model that leverages Seasonal-Trend Decomposition to link various types of anomalies to specific decomposition components, thereby simplifying the analysis of complex time-series and enhancing detection performance. Our training methodology, which includes pre-training on a synthetic dataset followed by fine-tuning, strikes a balance between effective decomposition and precise anomaly detection. Experimental validation on real-world datasets confirms TADNet's state-of-the-art performance across a diverse range of anomalies.

Linear Speedup of Incremental Aggregated Gradient Methods on Streaming Data

This paper considers a type of incremental aggregated gradient (IAG) method for large-scale distributed optimization. The IAG method is well suited for the parameter server architecture as the latter can easily aggregate potentially staled gradients contributed by workers. Although the convergence of IAG in the case of deterministic gradient is well known, there are only a few results for the case of its stochastic variant based on streaming data. Considering strongly convex optimization, this paper shows that the streaming IAG method achieves linear speedup when the workers are updating frequently enough, even if the data sample distribution across workers are heterogeneous. We show that the expected squared distance to optimal solution decays at O((1+T)/(nt)), where $n$ is the number of workers, t is the iteration number, and T/n is the update frequency of workers. Our analysis involves careful treatments of the conditional expectations with staled gradients and a recursive system with both delayed and noise terms, which are new to the analysis of IAG-type algorithms. Numerical results are presented to verify our findings.