Improving Diffusion-based Inverse Algorithms under Few-Step Constraint via Learnable Linear Extrapolation

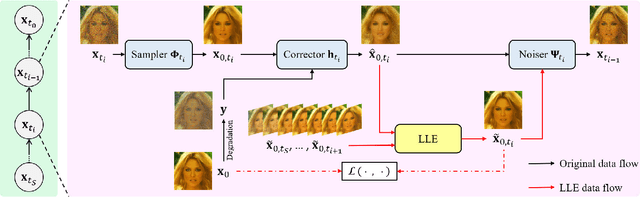
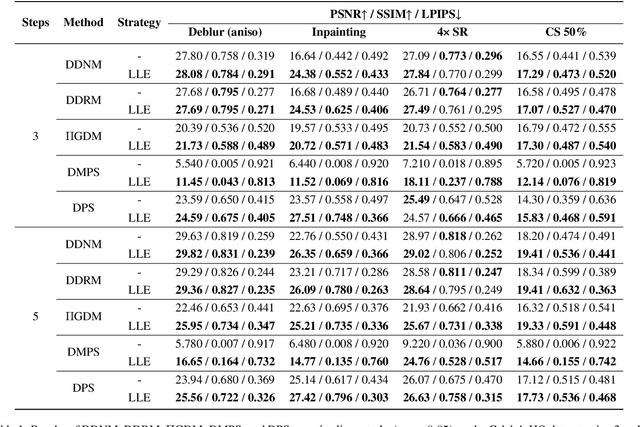
Diffusion models have demonstrated remarkable performance in modeling complex data priors, catalyzing their widespread adoption in solving various inverse problems. However, the inherently iterative nature of diffusion-based inverse algorithms often requires hundreds to thousands of steps, with performance degradation occurring under fewer steps which limits their practical applicability. While high-order diffusion ODE solvers have been extensively explored for efficient diffusion sampling without observations, their application to inverse problems remains underexplored due to the diverse forms of inverse algorithms and their need for repeated trajectory correction based on observations. To address this gap, we first introduce a canonical form that decomposes existing diffusion-based inverse algorithms into three modules to unify their analysis. Inspired by the linear subspace search strategy in the design of high-order diffusion ODE solvers, we propose the Learnable Linear Extrapolation (LLE) method, a lightweight approach that universally enhances the performance of any diffusion-based inverse algorithm that fits the proposed canonical form. Extensive experiments demonstrate consistent improvements of the proposed LLE method across multiple algorithms and tasks, indicating its potential for more efficient solutions and boosted performance of diffusion-based inverse algorithms with limited steps. Codes for reproducing our experiments are available at \href{https://github.com/weigerzan/LLE_inverse_problem}{https://github.com/weigerzan/LLE\_inverse\_problem}.