Phase transition for detecting a small community in a large network

How to detect a small community in a large network is an interesting problem, including clique detection as a special case, where a naive degree-based $\chi^2$-test was shown to be powerful in the presence of an Erd\H{o}s-Renyi background. Using Sinkhorn's theorem, we show that the signal captured by the $\chi^2$-test may be a modeling artifact, and it may disappear once we replace the Erd\H{o}s-Renyi model by a broader network model. We show that the recent SgnQ test is more appropriate for such a setting. The test is optimal in detecting communities with sizes comparable to the whole network, but has never been studied for our setting, which is substantially different and more challenging. Using a degree-corrected block model (DCBM), we establish phase transitions of this testing problem concerning the size of the small community and the edge densities in small and large communities. When the size of the small community is larger than $\sqrt{n}$, the SgnQ test is optimal for it attains the computational lower bound (CLB), the information lower bound for methods allowing polynomial computation time. When the size of the small community is smaller than $\sqrt{n}$, we establish the parameter regime where the SgnQ test has full power and make some conjectures of the CLB. We also study the classical information lower bound (LB) and show that there is always a gap between the CLB and LB in our range of interest.

Testing High-dimensional Multinomials with Applications to Text Analysis

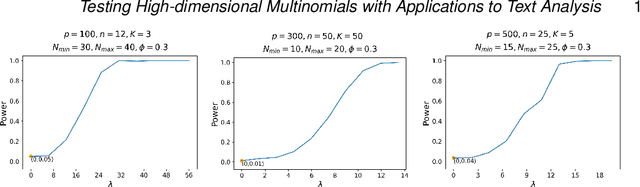
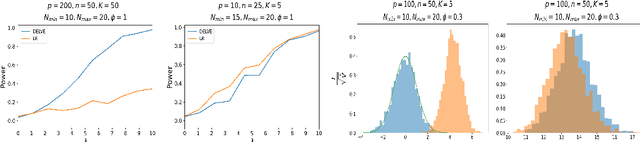
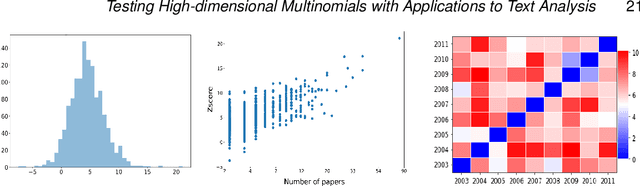
Motivated by applications in text mining and discrete distribution inference, we investigate the testing for equality of probability mass functions of $K$ groups of high-dimensional multinomial distributions. A test statistic, which is shown to have an asymptotic standard normal distribution under the null, is proposed. The optimal detection boundary is established, and the proposed test is shown to achieve this optimal detection boundary across the entire parameter space of interest. The proposed method is demonstrated in simulation studies and applied to analyze two real-world datasets to examine variation among consumer reviews of Amazon movies and diversity of statistical paper abstracts.

Near-optimal fitting of ellipsoids to random points

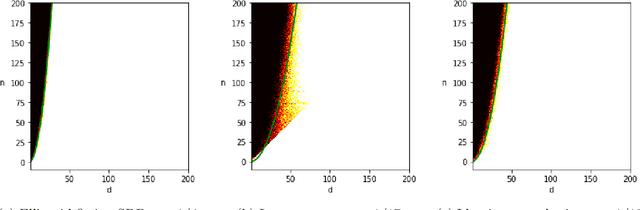
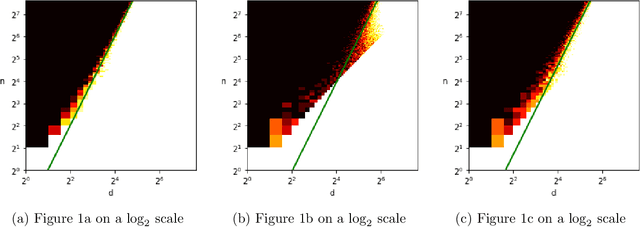
Given independent standard Gaussian points $v_1, \ldots, v_n$ in dimension $d$, for what values of $(n, d)$ does there exist with high probability an origin-symmetric ellipsoid that simultaneously passes through all of the points? This basic problem of fitting an ellipsoid to random points has connections to low-rank matrix decompositions, independent component analysis, and principal component analysis. Based on strong numerical evidence, Saunderson, Parrilo, and Willsky [Proc. of Conference on Decision and Control, pp. 6031-6036, 2013] conjecture that the ellipsoid fitting problem transitions from feasible to infeasible as the number of points $n$ increases, with a sharp threshold at $n \sim d^2/4$. We resolve this conjecture up to logarithmic factors by constructing a fitting ellipsoid for some $n = \Omega( \, d^2/\log^5(d) \,)$, improving prior work of Ghosh et al. [Proc. of Symposium on Foundations of Computer Science, pp. 954-965, 2020] that requires $n = o(d^{3/2})$. Our proof demonstrates feasibility of the least squares construction of Saunderson et al. using a careful analysis of the eigenvectors and eigenvalues of a certain non-standard random matrix.

Efficient Interpolation of Density Estimators

We study the problem of space and time efficient evaluation of a nonparametric estimator that approximates an unknown density. In the regime where consistent estimation is possible, we use a piecewise multivariate polynomial interpolation scheme to give a computationally efficient construction that converts the original estimator to a new estimator that can be queried efficiently and has low space requirements, all without adversely deteriorating the original approximation quality. Our result gives a new statistical perspective on the problem of fast evaluation of kernel density estimators in the presence of underlying smoothness. As a corollary, we give a succinct derivation of a classical result of Kolmogorov---Tikhomirov on the metric entropy of H\"{o}lder classes of smooth functions.

A Statistical Perspective on Coreset Density Estimation

Coresets have emerged as a powerful tool to summarize data by selecting a small subset of the original observations while retaining most of its information. This approach has led to significant computational speedups but the performance of statistical procedures run on coresets is largely unexplored. In this work, we develop a statistical framework to study coresets and focus on the canonical task of nonparameteric density estimation. Our contributions are twofold. First, we establish the minimax rate of estimation achievable by coreset-based estimators. Second, we show that the practical coreset kernel density estimators are near-minimax optimal over a large class of H\"{o}lder-smooth densities.

Efficient Reconstruction of Stochastic Pedigrees

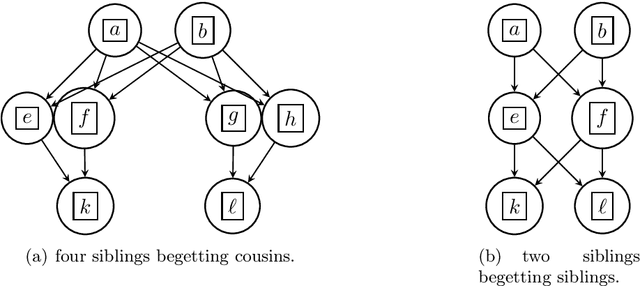
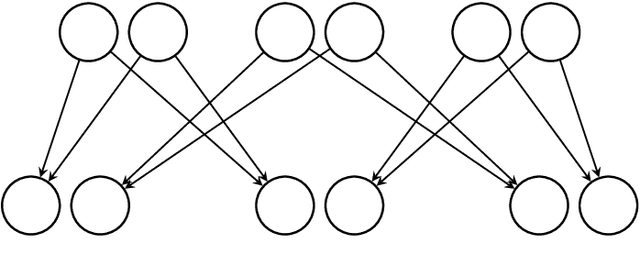
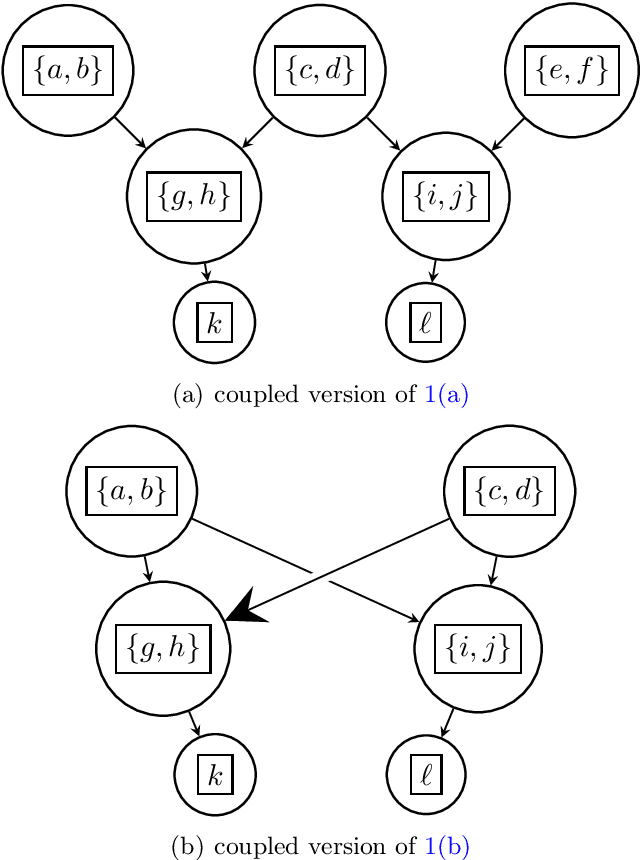
We introduce a new algorithm called {\sc Rec-Gen} for reconstructing the genealogy or \textit{pedigree} of an extant population purely from its genetic data. We justify our approach by giving a mathematical proof of the effectiveness of {\sc Rec-Gen} when applied to pedigrees from an idealized generative model that replicates some of the features of real-world pedigrees. Our algorithm is iterative and provides an accurate reconstruction of a large fraction of the pedigree while having relatively low \emph{sample complexity}, measured in terms of the length of the genetic sequences of the population. We propose our approach as a prototype for further investigation of the pedigree reconstruction problem toward the goal of applications to real-world examples. As such, our results have some conceptual bearing on the increasingly important issue of genomic privacy.