Feedback-Free Resource Scheduling: Towards Flexible Multi-BS Cooperation in FD-RAN

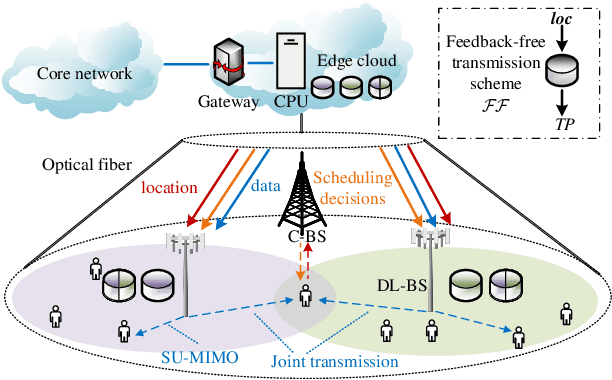
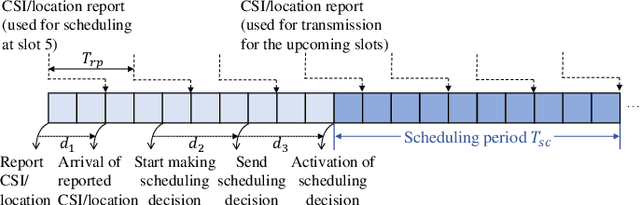
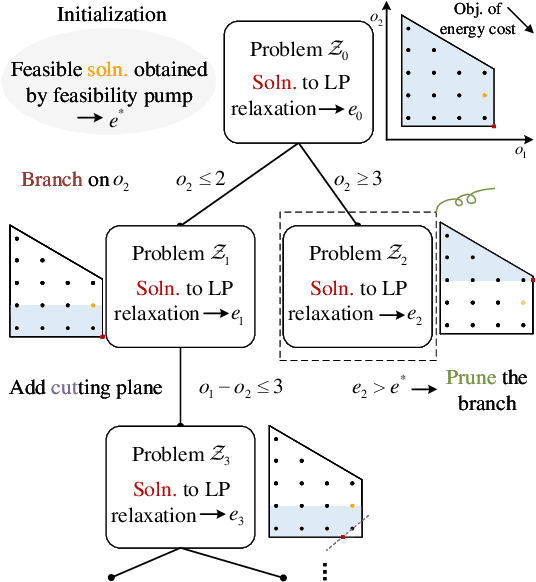
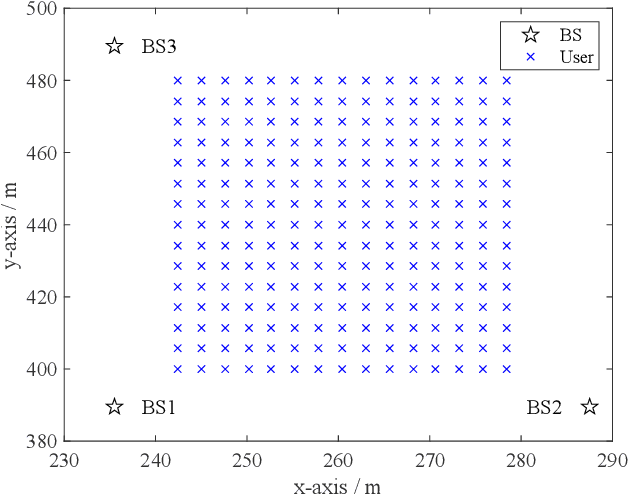
Flexible cooperation among base stations (BSs) is critical to improve resource utilization efficiency and meet personalized user demands. However, its practical implementation is hindered by the current radio access network (RAN), which relies on the coupling of uplink and downlink transmissions and channel state information feedback with inherent issues such as overheads and delays. To overcome these limitations, we consider the fully-decoupled RAN (FD-RAN), in which uplink and downlink networks are independent, and feedback-free MIMO transmission is adopted at the physical layer. To further deliver flexible cooperation in FD-RAN, we investigate the practical scheduling process and study feedback-free downlink multi-BS resource scheduling. The problem is considered based on network load conditions. In heavy-load states where it is impossible for all user demands to be met, an optimal greedy algorithm is proposed, maximizing the weighted sum of user demand satisfaction rates. In light-load states where at least one solution exists to satisfy all user demands, an optimal two-stage resource allocation algorithm is designed to further minimize network energy consumption by leveraging the flexibility of cooperation. Extensive simulations validate the superiority of proposed algorithms in performance and running time, and highlight the potential for realizing flexible cooperation in practice.

A Global Depth-Range-Free Multi-View Stereo Transformer Network with Pose Embedding

In this paper, we propose a novel multi-view stereo (MVS) framework that gets rid of the depth range prior. Unlike recent prior-free MVS methods that work in a pair-wise manner, our method simultaneously considers all the source images. Specifically, we introduce a Multi-view Disparity Attention (MDA) module to aggregate long-range context information within and across multi-view images. Considering the asymmetry of the epipolar disparity flow, the key to our method lies in accurately modeling multi-view geometric constraints. We integrate pose embedding to encapsulate information such as multi-view camera poses, providing implicit geometric constraints for multi-view disparity feature fusion dominated by attention. Additionally, we construct corresponding hidden states for each source image due to significant differences in the observation quality of the same pixel in the reference frame across multiple source frames. We explicitly estimate the quality of the current pixel corresponding to sampled points on the epipolar line of the source image and dynamically update hidden states through the uncertainty estimation module. Extensive results on the DTU dataset and Tanks&Temple benchmark demonstrate the effectiveness of our method. The code is available at our project page: https://zju3dv.github.io/GD-PoseMVS/.

Towards More Relevant Product Search Ranking Via Large Language Models: An Empirical Study

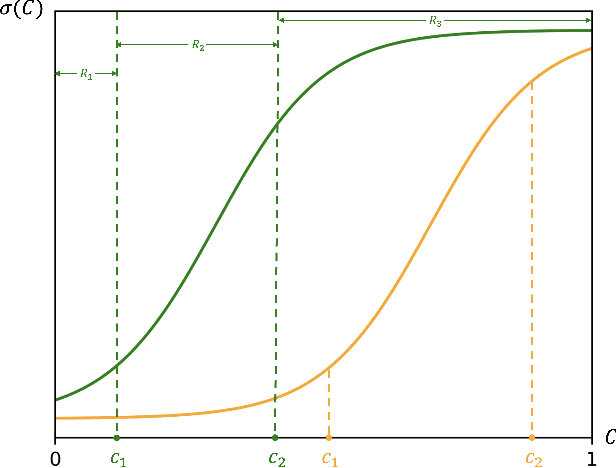
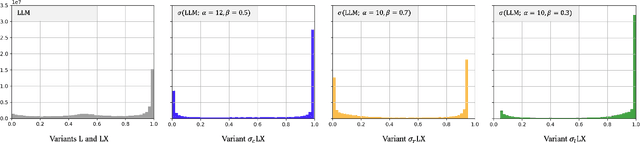
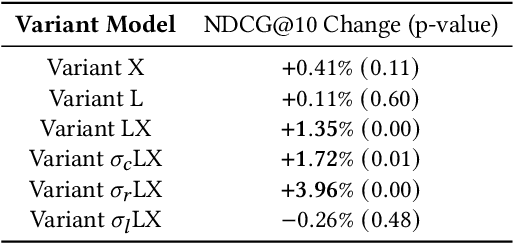
Training Learning-to-Rank models for e-commerce product search ranking can be challenging due to the lack of a gold standard of ranking relevance. In this paper, we decompose ranking relevance into content-based and engagement-based aspects, and we propose to leverage Large Language Models (LLMs) for both label and feature generation in model training, primarily aiming to improve the model's predictive capability for content-based relevance. Additionally, we introduce different sigmoid transformations on the LLM outputs to polarize relevance scores in labeling, enhancing the model's ability to balance content-based and engagement-based relevances and thus prioritize highly relevant items overall. Comprehensive online tests and offline evaluations are also conducted for the proposed design. Our work sheds light on advanced strategies for integrating LLMs into e-commerce product search ranking model training, offering a pathway to more effective and balanced models with improved ranking relevance.

Long or Short or Both? An Exploration on Lookback Time Windows of Behavioral Features in Product Search Ranking

Customer shopping behavioral features are core to product search ranking models in eCommerce. In this paper, we investigate the effect of lookback time windows when aggregating these features at the (query, product) level over history. By studying the pros and cons of using long and short time windows, we propose a novel approach to integrating these historical behavioral features of different time windows. In particular, we address the criticality of using query-level vertical signals in ranking models to effectively aggregate all information from different behavioral features. Anecdotal evidence for the proposed approach is also provided using live product search traffic on Walmart.com.

Stability of a Generalized Debiased Lasso with Applications to Resampling-Based Variable Selection

Suppose that we first apply the Lasso to a design matrix, and then update one of its columns. In general, the signs of the Lasso coefficients may change, and there is no closed-form expression for updating the Lasso solution exactly. In this work, we propose an approximate formula for updating a debiased Lasso coefficient. We provide general nonasymptotic error bounds in terms of the norms and correlations of a given design matrix's columns, and then prove asymptotic convergence results for the case of a random design matrix with i.i.d.\ sub-Gaussian row vectors and i.i.d.\ Gaussian noise. Notably, the approximate formula is asymptotically correct for most coordinates in the proportional growth regime, under the mild assumption that each row of the design matrix is sub-Gaussian with a covariance matrix having a bounded condition number. Our proof only requires certain concentration and anti-concentration properties to control various error terms and the number of sign changes. In contrast, rigorously establishing distributional limit properties (e.g.\ Gaussian limits for the debiased Lasso) under similarly general assumptions has been considered open problem in the universality theory. As applications, we show that the approximate formula allows us to reduce the computation complexity of variable selection algorithms that require solving multiple Lasso problems, such as the conditional randomization test and a variant of the knockoff filter.

Minimax Optimality of Score-based Diffusion Models: Beyond the Density Lower Bound Assumptions

We study the asymptotic error of score-based diffusion model sampling in large-sample scenarios from a non-parametric statistics perspective. We show that a kernel-based score estimator achieves an optimal mean square error of $\widetilde{O}\left(n^{-1} t^{-\frac{d+2}{2}}(t^{\frac{d}{2}} \vee 1)\right)$ for the score function of $p_0*\mathcal{N}(0,t\boldsymbol{I}_d)$, where $n$ and $d$ represent the sample size and the dimension, $t$ is bounded above and below by polynomials of $n$, and $p_0$ is an arbitrary sub-Gaussian distribution. As a consequence, this yields an $\widetilde{O}\left(n^{-1/2} t^{-\frac{d}{4}}\right)$ upper bound for the total variation error of the distribution of the sample generated by the diffusion model under a mere sub-Gaussian assumption. If in addition, $p_0$ belongs to the nonparametric family of the $\beta$-Sobolev space with $\beta\le 2$, by adopting an early stopping strategy, we obtain that the diffusion model is nearly (up to log factors) minimax optimal. This removes the crucial lower bound assumption on $p_0$ in previous proofs of the minimax optimality of the diffusion model for nonparametric families.

$L^1$ Estimation: On the Optimality of Linear Estimators

Consider the problem of estimating a random variable $X$ from noisy observations $Y = X+ Z$, where $Z$ is standard normal, under the $L^1$ fidelity criterion. It is well known that the optimal Bayesian estimator in this setting is the conditional median. This work shows that the only prior distribution on $X$ that induces linearity in the conditional median is Gaussian. Along the way, several other results are presented. In particular, it is demonstrated that if the conditional distribution $P_{X|Y=y}$ is symmetric for all $y$, then $X$ must follow a Gaussian distribution. Additionally, we consider other $L^p$ losses and observe the following phenomenon: for $p \in [1,2]$, Gaussian is the only prior distribution that induces a linear optimal Bayesian estimator, and for $p \in (2,\infty)$, infinitely many prior distributions on $X$ can induce linearity. Finally, extensions are provided to encompass noise models leading to conditional distributions from certain exponential families.

NeILF++: Inter-Reflectable Light Fields for Geometry and Material Estimation

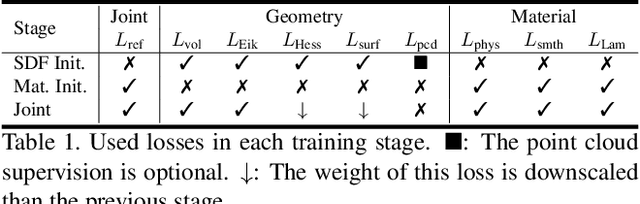
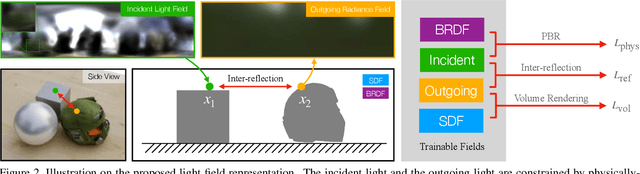
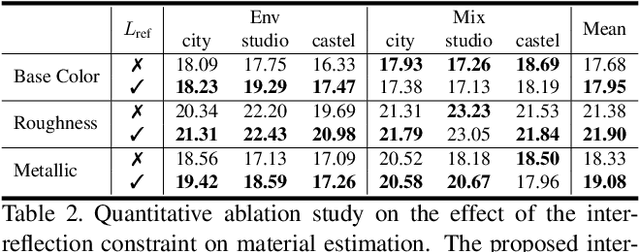
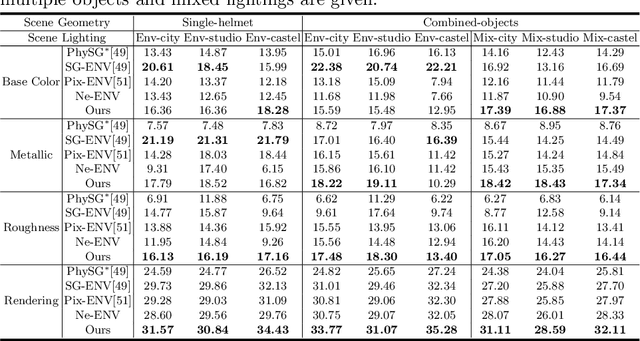
We present a novel differentiable rendering framework for joint geometry, material, and lighting estimation from multi-view images. In contrast to previous methods which assume a simplified environment map or co-located flashlights, in this work, we formulate the lighting of a static scene as one neural incident light field (NeILF) and one outgoing neural radiance field (NeRF). The key insight of the proposed method is the union of the incident and outgoing light fields through physically-based rendering and inter-reflections between surfaces, making it possible to disentangle the scene geometry, material, and lighting from image observations in a physically-based manner. The proposed incident light and inter-reflection framework can be easily applied to other NeRF systems. We show that our method can not only decompose the outgoing radiance into incident lights and surface materials, but also serve as a surface refinement module that further improves the reconstruction detail of the neural surface. We demonstrate on several datasets that the proposed method is able to achieve state-of-the-art results in terms of geometry reconstruction quality, material estimation accuracy, and the fidelity of novel view rendering.

NeILF: Neural Incident Light Field for Physically-based Material Estimation

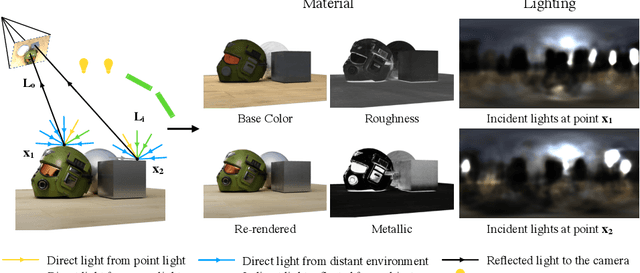
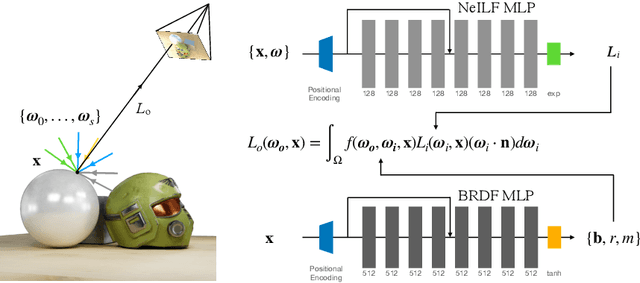
We present a differentiable rendering framework for material and lighting estimation from multi-view images and a reconstructed geometry. In the framework, we represent scene lightings as the Neural Incident Light Field (NeILF) and material properties as the surface BRDF modelled by multi-layer perceptrons. Compared with recent approaches that approximate scene lightings as the 2D environment map, NeILF is a fully 5D light field that is capable of modelling illuminations of any static scenes. In addition, occlusions and indirect lights can be handled naturally by the NeILF representation without requiring multiple bounces of ray tracing, making it possible to estimate material properties even for scenes with complex lightings and geometries. We also propose a smoothness regularization and a Lambertian assumption to reduce the material-lighting ambiguity during the optimization. Our method strictly follows the physically-based rendering equation, and jointly optimizes material and lighting through the differentiable rendering process. We have intensively evaluated the proposed method on our in-house synthetic dataset, the DTU MVS dataset, and real-world BlendedMVS scenes. Our method is able to outperform previous methods by a significant margin in terms of novel view rendering quality, setting a new state-of-the-art for image-based material and lighting estimation.

Efficient Interpolation of Density Estimators

We study the problem of space and time efficient evaluation of a nonparametric estimator that approximates an unknown density. In the regime where consistent estimation is possible, we use a piecewise multivariate polynomial interpolation scheme to give a computationally efficient construction that converts the original estimator to a new estimator that can be queried efficiently and has low space requirements, all without adversely deteriorating the original approximation quality. Our result gives a new statistical perspective on the problem of fast evaluation of kernel density estimators in the presence of underlying smoothness. As a corollary, we give a succinct derivation of a classical result of Kolmogorov---Tikhomirov on the metric entropy of H\"{o}lder classes of smooth functions.