Generalized Linear Models with 1-Bit Measurements: Asymptotics of the Maximum Likelihood Estimator

This work establishes regularity conditions for consistency and asymptotic normality of the multiple parameter maximum likelihood estimator(MLE) from censored data, where the censoring mechanism is in the form of $1$-bit measurements. The underlying distribution of the uncensored data is assumed to belong to the exponential family, with natural parameters expressed as a linear combination of the predictors, known as generalized linear model (GLM). As part of the analysis, the Fisher information matrix is also derived for both censored and uncensored data, which helps to quantify the impact of censoring and assess the performance of the MLE. The choice of GLM allows one to consider a variety of practical examples where 1-bit estimation is of interest. In particular, it is shown how the derived results can be used to analyze two practically relevant scenarios: the Gaussian model with both unknown mean and variance, and the Poisson model with an unknown mean.

A Comprehensive Study on Ziv-Zakai Lower Bounds on the MMSE

This paper explores Bayesian lower bounds on the minimum mean squared error (MMSE) that belong to the Ziv-Zakai (ZZ) family. The ZZ technique relies on connecting the bound to an M-ary hypothesis testing problem. Three versions of the ZZ bound (ZZB) exist: the first relies on the so-called valley-filling function (VFF), the second omits the VFF, and the third, i.e., the single-point ZZB (SZZB), uses a single point maximization. The first part of this paper provides the most general version of the bounds. First, it is shown that these bounds hold without any assumption on the distribution of the estimand. Second, the SZZB bound is extended to an M-ary setting and a version of it for the multivariate case is provided. In the second part, general properties of the bounds are provided. First, it is shown that all the bounds tensorize. Second, a complete characterization of the high-noise asymptotic is provided, which is used to argue about the tightness of the bounds. Third, the low-noise asymptotic is provided for mixed-input distributions and Gaussian additive noise channels. Specifically, in the low-noise, it is shown that the SZZB is not always tight. In the third part, the tightness of the bounds is evaluated. First, it is shown that in the low-noise regime the ZZB bound without the VFF is tight for mixed-input distributions and Gaussian additive noise channels. Second, for discrete inputs, the ZZB with the VFF is shown to be always sub-optimal, and equal to zero without the VFF. Third, unlike for the ZZB, an example is shown for which the SZZB is tight to the MMSE for discrete inputs. Fourth, sufficient and necessary conditions for the tightness of the bounds are provided. Finally, some examples are shown in which the bounds in the ZZ family outperform other well-known Bayesian bounds, i.e., the Cram\'er-Rao bound and the maximum entropy bound.

Data-Driven Estimation of the False Positive Rate of the Bayes Binary Classifier via Soft Labels

Classification is a fundamental task in many applications on which data-driven methods have shown outstanding performances. However, it is challenging to determine whether such methods have achieved the optimal performance. This is mainly because the best achievable performance is typically unknown and hence, effectively estimating it is of prime importance. In this paper, we consider binary classification problems and we propose an estimator for the false positive rate (FPR) of the Bayes classifier, that is, the optimal classifier with respect to accuracy, from a given dataset. Our method utilizes soft labels, or real-valued labels, which are gaining significant traction thanks to their properties. We thoroughly examine various theoretical properties of our estimator, including its consistency, unbiasedness, rate of convergence, and variance. To enhance the versatility of our estimator beyond soft labels, we also consider noisy labels, which encompass binary labels. For noisy labels, we develop effective FPR estimators by leveraging a denoising technique and the Nadaraya-Watson estimator. Due to the symmetry of the problem, our results can be readily applied to estimate the false negative rate of the Bayes classifier.

$L^1$ Estimation: On the Optimality of Linear Estimators

Consider the problem of estimating a random variable $X$ from noisy observations $Y = X+ Z$, where $Z$ is standard normal, under the $L^1$ fidelity criterion. It is well known that the optimal Bayesian estimator in this setting is the conditional median. This work shows that the only prior distribution on $X$ that induces linearity in the conditional median is Gaussian. Along the way, several other results are presented. In particular, it is demonstrated that if the conditional distribution $P_{X|Y=y}$ is symmetric for all $y$, then $X$ must follow a Gaussian distribution. Additionally, we consider other $L^p$ losses and observe the following phenomenon: for $p \in [1,2]$, Gaussian is the only prior distribution that induces a linear optimal Bayesian estimator, and for $p \in (2,\infty)$, infinitely many prior distributions on $X$ can induce linearity. Finally, extensions are provided to encompass noise models leading to conditional distributions from certain exponential families.

Functional Properties of the Ziv-Zakai bound with Arbitrary Inputs

This paper explores the Ziv-Zakai bound (ZZB), which is a well-known Bayesian lower bound on the Minimum Mean Squared Error (MMSE). First, it is shown that the ZZB holds without any assumption on the distribution of the estimand, that is, the estimand does not necessarily need to have a probability density function. The ZZB is then further analyzed in the high-noise and low-noise regimes and shown to always tensorize. Finally, the tightness of the ZZB is investigated under several aspects, such as the number of hypotheses and the usefulness of the valley-filling function. In particular, a sufficient and necessary condition for the tightness of the bound with continuous inputs is provided, and it is shown that the bound is never tight for discrete input distributions with a support set that does not have an accumulation point at zero.

An MMSE Lower Bound via Poincaré Inequality

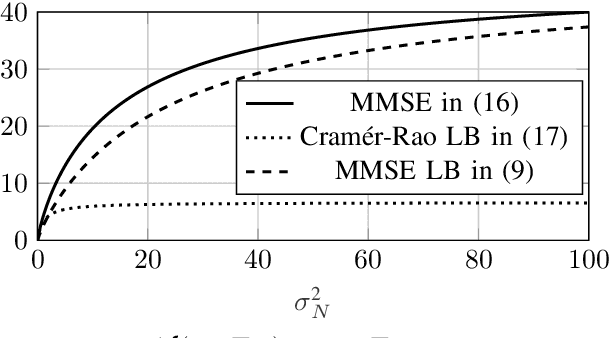
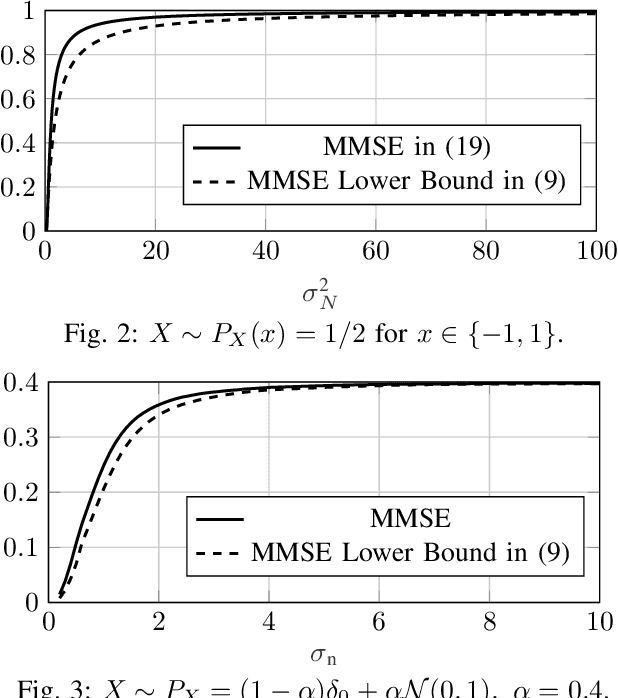
This paper studies the minimum mean squared error (MMSE) of estimating $\mathbf{X} \in \mathbb{R}^d$ from the noisy observation $\mathbf{Y} \in \mathbb{R}^k$, under the assumption that the noise (i.e., $\mathbf{Y}|\mathbf{X}$) is a member of the exponential family. The paper provides a new lower bound on the MMSE. Towards this end, an alternative representation of the MMSE is first presented, which is argued to be useful in deriving closed-form expressions for the MMSE. This new representation is then used together with the Poincar\'e inequality to provide a new lower bound on the MMSE. Unlike, for example, the Cram\'{e}r-Rao bound, the new bound holds for all possible distributions on the input $\mathbf{X}$. Moreover, the lower bound is shown to be tight in the high-noise regime for the Gaussian noise setting under the assumption that $\mathbf{X}$ is sub-Gaussian. Finally, several numerical examples are shown which demonstrate that the bound performs well in all noise regimes.

Entropic CLT for Order Statistics

It is well known that central order statistics exhibit a central limit behavior and converge to a Gaussian distribution as the sample size grows. This paper strengthens this known result by establishing an entropic version of the CLT that ensures a stronger mode of convergence using the relative entropy. In particular, an order $O(1/\sqrt{n})$ rate of convergence is established under mild conditions on the parent distribution of the sample generating the order statistics. To prove this result, ancillary results on order statistics are derived, which might be of independent interest.

A Dimensionality Reduction Method for Finding Least Favorable Priors with a Focus on Bregman Divergence

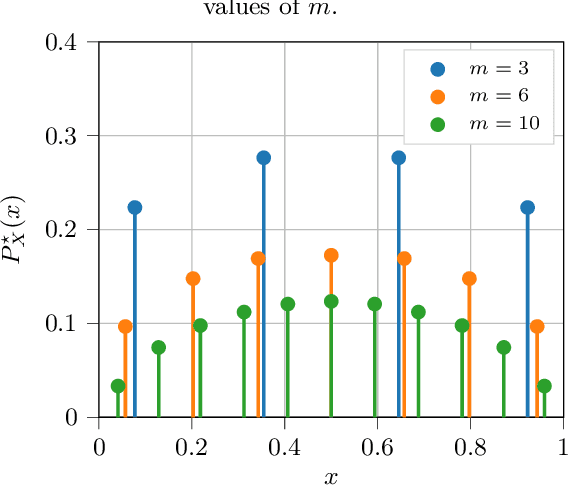
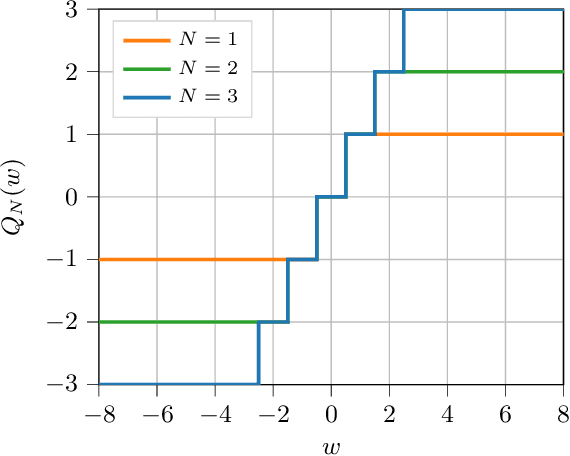
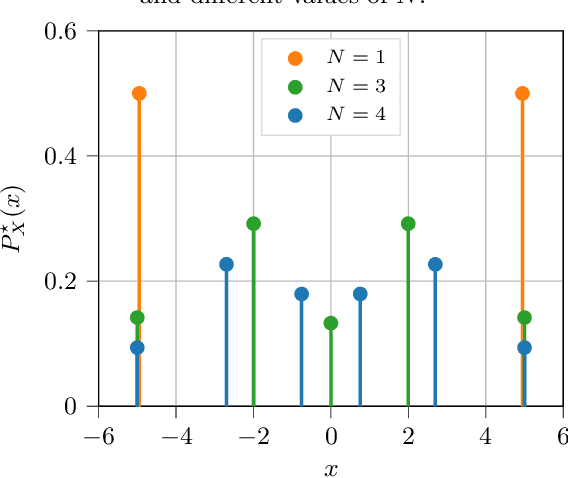
A common way of characterizing minimax estimators in point estimation is by moving the problem into the Bayesian estimation domain and finding a least favorable prior distribution. The Bayesian estimator induced by a least favorable prior, under mild conditions, is then known to be minimax. However, finding least favorable distributions can be challenging due to inherent optimization over the space of probability distributions, which is infinite-dimensional. This paper develops a dimensionality reduction method that allows us to move the optimization to a finite-dimensional setting with an explicit bound on the dimension. The benefit of this dimensionality reduction is that it permits the use of popular algorithms such as projected gradient ascent to find least favorable priors. Throughout the paper, in order to make progress on the problem, we restrict ourselves to Bayesian risks induced by a relatively large class of loss functions, namely Bregman divergences.

Improved Information Theoretic Generalization Bounds for Distributed and Federated Learning

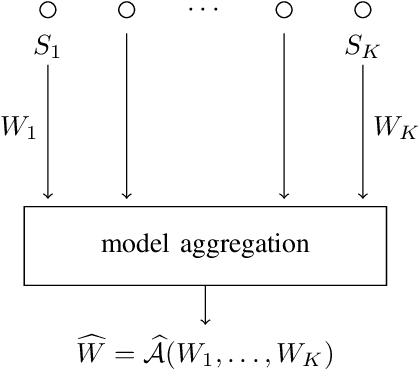
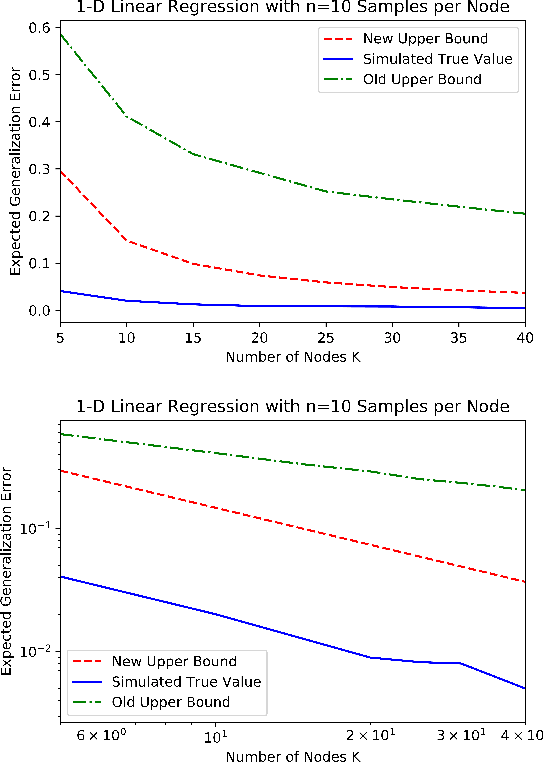
We consider information-theoretic bounds on expected generalization error for statistical learning problems in a networked setting. In this setting, there are $K$ nodes, each with its own independent dataset, and the models from each node have to be aggregated into a final centralized model. We consider both simple averaging of the models as well as more complicated multi-round algorithms. We give upper bounds on the expected generalization error for a variety of problems, such as those with Bregman divergence or Lipschitz continuous losses, that demonstrate an improved dependence of $1/K$ on the number of nodes. These "per node" bounds are in terms of the mutual information between the training dataset and the trained weights at each node, and are therefore useful in describing the generalization properties inherent to having communication or privacy constraints at each node.

Consistent Density Estimation Under Discrete Mixture Models

This work considers a problem of estimating a mixing probability density $f$ in the setting of discrete mixture models. The paper consists of three parts. The first part focuses on the construction of an $L_1$ consistent estimator of $f$. In particular, under the assumptions that the probability measure $\mu$ of the observation is atomic, and the map from $f$ to $\mu$ is bijective, it is shown that there exists an estimator $f_n$ such that for every density $f$ $\lim_{n\to \infty} \mathbb{E} \left[ \int |f_n -f | \right]=0$. The second part discusses the implementation details. Specifically, it is shown that the consistency for every $f$ can be attained with a computationally feasible estimator. The third part, as a study case, considers a Poisson mixture model. In particular, it is shown that in the Poisson noise setting, the bijection condition holds and, hence, estimation can be performed consistently for every $f$.