Estimating Mutual Information between Time Series and Temporal Event Sequences Across Diverse Analysis Tasks

Pairwise dependence measures such as correlation and causality are fundamental to temporal data mining, yet there is still no principled and robust way to quantify dependence between heterogeneous data types, especially between continuous time series and discrete temporal event sequences. Existing approaches rely on ad hoc transformations or mutual-information estimators that are highly sensitive to quantization, repeated values, and event redundancy, leading to biased or unstable results in practice. We propose a nonparametric mutual information estimator that directly measures the dependence between time series and event sequences without data transformation, learning, or ad hoc discretization. Our method models the continuous-discrete duality of real-world time series to handle quantization and repeated-value artifacts and introduces a latent event clustering strategy to mitigate bias from event co-occurrence and redundancy. Together, these yield a robust and unified framework that bridges discrete and continuous mutual information. We evaluate the proposed estimator on four representative tasks: discrete-continuous time-delayed mutual information for causality analysis, global and local temporal repetition discovery, discrete covariate selection for time series forecasting, and continuous feature selection for classification. Experiments on synthetic and real-world datasets show consistent improvements over existing methods in accuracy, robustness, and interpretability, positioning our approach as a general-purpose dependence operator for heterogeneous temporal data, similar to Pearson correlation for homogeneous time series. Code available at: https://github.com/HaojiHu/Multimodal-Temporal-Data-Quantification

Generalizing Supervised Contrastive learning: A Projection Perspective

Self-supervised contrastive learning (SSCL) has emerged as a powerful paradigm for representation learning and has been studied from multiple perspectives, including mutual information and geometric viewpoints. However, supervised contrastive (SupCon) approaches have received comparatively little attention in this context: for instance, while InfoNCE used in SSCL is known to form a lower bound on mutual information (MI), the relationship between SupCon and MI remains unexplored. To address this gap, we introduce ProjNCE, a generalization of the InfoNCE loss that unifies supervised and self-supervised contrastive objectives by incorporating projection functions and an adjustment term for negative pairs. We prove that ProjNCE constitutes a valid MI bound and affords greater flexibility in selecting projection strategies for class embeddings. Building on this flexibility, we further explore the centroid-based class embeddings in SupCon by exploring a variety of projection methods. Extensive experiments on multiple datasets and settings demonstrate that ProjNCE consistently outperforms both SupCon and standard cross-entropy training. Our work thus refines SupCon along two complementary perspective--mutual information interpretation and projection design--and offers broadly applicable improvements whenever SupCon serves as the foundational contrastive objective.

Probabilistic Variational Contrastive Learning

Deterministic embeddings learned by contrastive learning (CL) methods such as SimCLR and SupCon achieve state-of-the-art performance but lack a principled mechanism for uncertainty quantification. We propose Variational Contrastive Learning (VCL), a decoder-free framework that maximizes the evidence lower bound (ELBO) by interpreting the InfoNCE loss as a surrogate reconstruction term and adding a KL divergence regularizer to a uniform prior on the unit hypersphere. We model the approximate posterior $q_\theta(z|x)$ as a projected normal distribution, enabling the sampling of probabilistic embeddings. Our two instantiations--VSimCLR and VSupCon--replace deterministic embeddings with samples from $q_\theta(z|x)$ and incorporate a normalized KL term into the loss. Experiments on multiple benchmarks demonstrate that VCL mitigates dimensional collapse, enhances mutual information with class labels, and matches or outperforms deterministic baselines in classification accuracy, all the while providing meaningful uncertainty estimates through the posterior model. VCL thus equips contrastive learning with a probabilistic foundation, serving as a new basis for contrastive approaches.

Anchors Aweigh! Sail for Optimal Unified Multi-Modal Representations

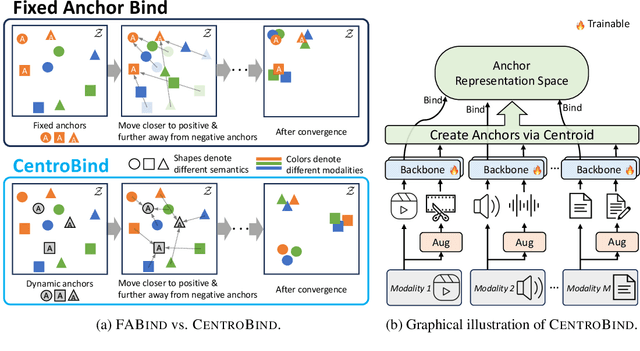
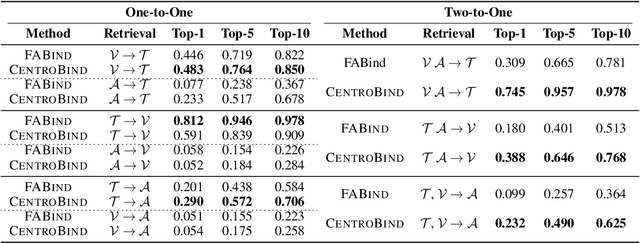
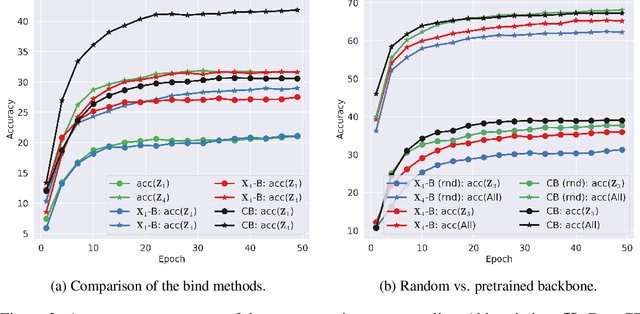
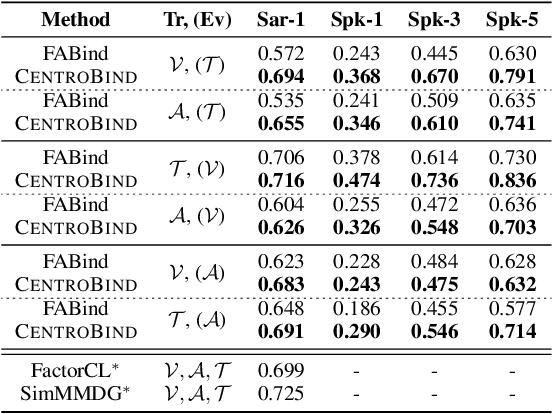
Multimodal learning plays a crucial role in enabling machine learning models to fuse and utilize diverse data sources, such as text, images, and audio, to support a variety of downstream tasks. A unified representation across various modalities is particularly important for improving efficiency and performance. Recent binding methods, such as ImageBind (Girdhar et al., 2023), typically use a fixed anchor modality to align multimodal data in the anchor modal embedding space. In this paper, we mathematically analyze the fixed anchor binding methods and uncover notable limitations: (1) over-reliance on the choice of the anchor modality, (2) failure to capture intra-modal information, and (3) failure to account for inter-modal correlation among non-anchored modalities. To address these limitations, we propose CentroBind, a simple yet powerful approach that eliminates the need for a fixed anchor; instead, it employs dynamically adjustable centroid-based anchors generated from all available modalities, resulting in a balanced and rich representation space. We theoretically demonstrate that our method captures three crucial properties of multimodal learning: intra-modal learning, inter-modal learning, and multimodal alignment, while also constructing a robust unified representation across all modalities. Our experiments on both synthetic and real-world datasets demonstrate the superiority of the proposed method, showing that dynamic anchor methods outperform all fixed anchor binding methods as the former captures more nuanced multimodal interactions.

A Comprehensive Study on Ziv-Zakai Lower Bounds on the MMSE

This paper explores Bayesian lower bounds on the minimum mean squared error (MMSE) that belong to the Ziv-Zakai (ZZ) family. The ZZ technique relies on connecting the bound to an M-ary hypothesis testing problem. Three versions of the ZZ bound (ZZB) exist: the first relies on the so-called valley-filling function (VFF), the second omits the VFF, and the third, i.e., the single-point ZZB (SZZB), uses a single point maximization. The first part of this paper provides the most general version of the bounds. First, it is shown that these bounds hold without any assumption on the distribution of the estimand. Second, the SZZB bound is extended to an M-ary setting and a version of it for the multivariate case is provided. In the second part, general properties of the bounds are provided. First, it is shown that all the bounds tensorize. Second, a complete characterization of the high-noise asymptotic is provided, which is used to argue about the tightness of the bounds. Third, the low-noise asymptotic is provided for mixed-input distributions and Gaussian additive noise channels. Specifically, in the low-noise, it is shown that the SZZB is not always tight. In the third part, the tightness of the bounds is evaluated. First, it is shown that in the low-noise regime the ZZB bound without the VFF is tight for mixed-input distributions and Gaussian additive noise channels. Second, for discrete inputs, the ZZB with the VFF is shown to be always sub-optimal, and equal to zero without the VFF. Third, unlike for the ZZB, an example is shown for which the SZZB is tight to the MMSE for discrete inputs. Fourth, sufficient and necessary conditions for the tightness of the bounds are provided. Finally, some examples are shown in which the bounds in the ZZ family outperform other well-known Bayesian bounds, i.e., the Cram\'er-Rao bound and the maximum entropy bound.

Data-Driven Estimation of the False Positive Rate of the Bayes Binary Classifier via Soft Labels

Classification is a fundamental task in many applications on which data-driven methods have shown outstanding performances. However, it is challenging to determine whether such methods have achieved the optimal performance. This is mainly because the best achievable performance is typically unknown and hence, effectively estimating it is of prime importance. In this paper, we consider binary classification problems and we propose an estimator for the false positive rate (FPR) of the Bayes classifier, that is, the optimal classifier with respect to accuracy, from a given dataset. Our method utilizes soft labels, or real-valued labels, which are gaining significant traction thanks to their properties. We thoroughly examine various theoretical properties of our estimator, including its consistency, unbiasedness, rate of convergence, and variance. To enhance the versatility of our estimator beyond soft labels, we also consider noisy labels, which encompass binary labels. For noisy labels, we develop effective FPR estimators by leveraging a denoising technique and the Nadaraya-Watson estimator. Due to the symmetry of the problem, our results can be readily applied to estimate the false negative rate of the Bayes classifier.

Functional Properties of the Ziv-Zakai bound with Arbitrary Inputs

This paper explores the Ziv-Zakai bound (ZZB), which is a well-known Bayesian lower bound on the Minimum Mean Squared Error (MMSE). First, it is shown that the ZZB holds without any assumption on the distribution of the estimand, that is, the estimand does not necessarily need to have a probability density function. The ZZB is then further analyzed in the high-noise and low-noise regimes and shown to always tensorize. Finally, the tightness of the ZZB is investigated under several aspects, such as the number of hypotheses and the usefulness of the valley-filling function. In particular, a sufficient and necessary condition for the tightness of the bound with continuous inputs is provided, and it is shown that the bound is never tight for discrete input distributions with a support set that does not have an accumulation point at zero.

Retrieving Data Permutations from Noisy Observations: High and Low Noise Asymptotics

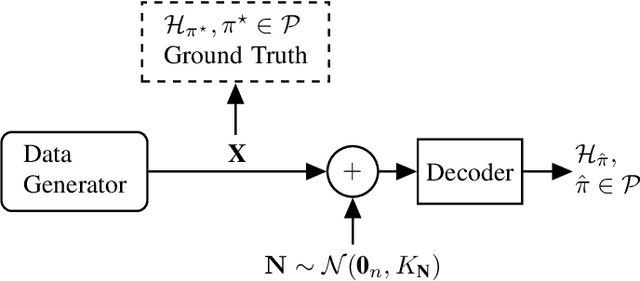
This paper considers the problem of recovering the permutation of an n-dimensional random vector X observed in Gaussian noise. First, a general expression for the probability of error is derived when a linear decoder (i.e., linear estimator followed by a sorting operation) is used. The derived expression holds with minimal assumptions on the distribution of X and when the noise has memory. Second, for the case of isotropic noise (i.e., noise with a diagonal scalar covariance matrix), the rates of convergence of the probability of error are characterized in the high and low noise regimes. In the low noise regime, for every dimension n, the probability of error is shown to behave proportionally to {\sigma}, where {\sigma} is the noise standard deviation. Moreover, the slope is computed exactly for several distributions and it is shown to behave quadratically in n. In the high noise regime, for every dimension n, the probability of correctness is shown to behave as 1/{\sigma}, and the exact expression for the rate of convergence is also provided.