Retrieving Data Permutations from Noisy Observations: High and Low Noise Asymptotics
Paper and Code
May 07, 2021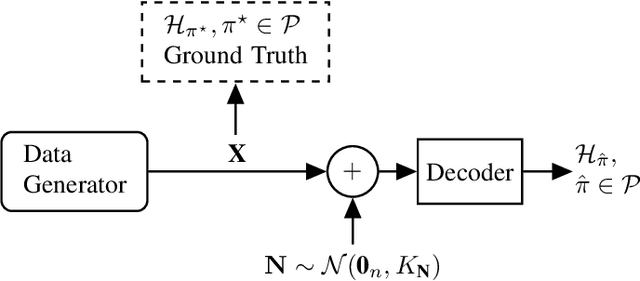
This paper considers the problem of recovering the permutation of an n-dimensional random vector X observed in Gaussian noise. First, a general expression for the probability of error is derived when a linear decoder (i.e., linear estimator followed by a sorting operation) is used. The derived expression holds with minimal assumptions on the distribution of X and when the noise has memory. Second, for the case of isotropic noise (i.e., noise with a diagonal scalar covariance matrix), the rates of convergence of the probability of error are characterized in the high and low noise regimes. In the low noise regime, for every dimension n, the probability of error is shown to behave proportionally to {\sigma}, where {\sigma} is the noise standard deviation. Moreover, the slope is computed exactly for several distributions and it is shown to behave quadratically in n. In the high noise regime, for every dimension n, the probability of correctness is shown to behave as 1/{\sigma}, and the exact expression for the rate of convergence is also provided.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge