Ian Zieder
An MMSE Lower Bound via Poincaré Inequality
May 12, 2022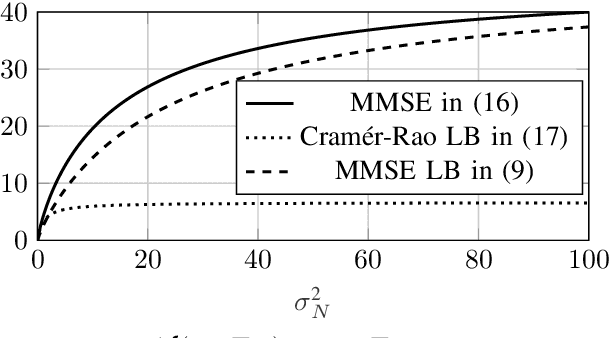
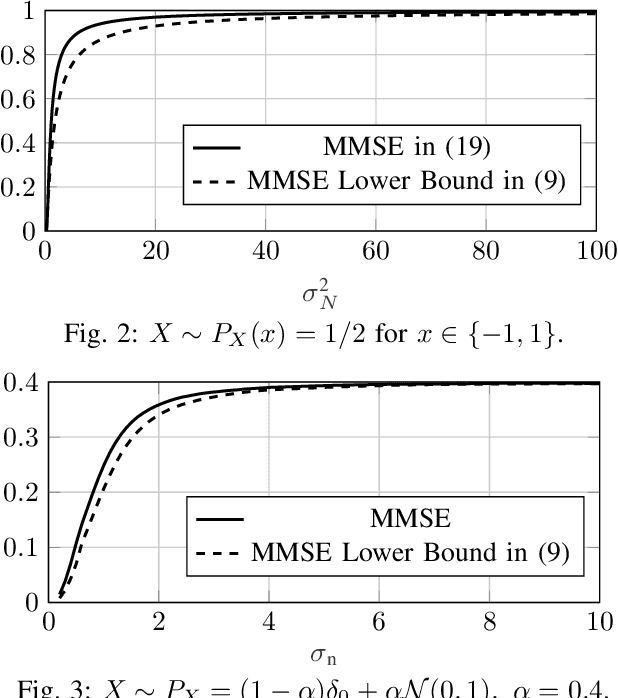
Abstract:This paper studies the minimum mean squared error (MMSE) of estimating $\mathbf{X} \in \mathbb{R}^d$ from the noisy observation $\mathbf{Y} \in \mathbb{R}^k$, under the assumption that the noise (i.e., $\mathbf{Y}|\mathbf{X}$) is a member of the exponential family. The paper provides a new lower bound on the MMSE. Towards this end, an alternative representation of the MMSE is first presented, which is argued to be useful in deriving closed-form expressions for the MMSE. This new representation is then used together with the Poincar\'e inequality to provide a new lower bound on the MMSE. Unlike, for example, the Cram\'{e}r-Rao bound, the new bound holds for all possible distributions on the input $\mathbf{X}$. Moreover, the lower bound is shown to be tight in the high-noise regime for the Gaussian noise setting under the assumption that $\mathbf{X}$ is sub-Gaussian. Finally, several numerical examples are shown which demonstrate that the bound performs well in all noise regimes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge