Near-Optimal differentially private low-rank trace regression with guaranteed private initialization

We study differentially private (DP) estimation of a rank-$r$ matrix $M \in \mathbb{R}^{d_1\times d_2}$ under the trace regression model with Gaussian measurement matrices. Theoretically, the sensitivity of non-private spectral initialization is precisely characterized, and the differential-privacy-constrained minimax lower bound for estimating $M$ under the Schatten-$q$ norm is established. Methodologically, the paper introduces a computationally efficient algorithm for DP-initialization with a sample size of $n \geq \widetilde O (r^2 (d_1\vee d_2))$. Under certain regularity conditions, the DP-initialization falls within a local ball surrounding $M$. We also propose a differentially private algorithm for estimating $M$ based on Riemannian optimization (DP-RGrad), which achieves a near-optimal convergence rate with the DP-initialization and sample size of $n \geq \widetilde O(r (d_1 + d_2))$. Finally, the paper discusses the non-trivial gap between the minimax lower bound and the upper bound of low-rank matrix estimation under the trace regression model. It is shown that the estimator given by DP-RGrad attains the optimal convergence rate in a weaker notion of differential privacy. Our powerful technique for analyzing the sensitivity of initialization requires no eigengap condition between $r$ non-zero singular values.

Optimal Differentially Private PCA and Estimation for Spiked Covariance Matrices

Estimating a covariance matrix and its associated principal components is a fundamental problem in contemporary statistics. While optimal estimation procedures have been developed with well-understood properties, the increasing demand for privacy preservation introduces new complexities to this classical problem. In this paper, we study optimal differentially private Principal Component Analysis (PCA) and covariance estimation within the spiked covariance model. We precisely characterize the sensitivity of eigenvalues and eigenvectors under this model and establish the minimax rates of convergence for estimating both the principal components and covariance matrix. These rates hold up to logarithmic factors and encompass general Schatten norms, including spectral norm, Frobenius norm, and nuclear norm as special cases. We introduce computationally efficient differentially private estimators and prove their minimax optimality, up to logarithmic factors. Additionally, matching minimax lower bounds are established. Notably, in comparison with existing literature, our results accommodate a diverging rank, necessitate no eigengap condition between distinct principal components, and remain valid even if the sample size is much smaller than the dimension.

IDEA: Interpretable Dynamic Ensemble Architecture for Time Series Prediction

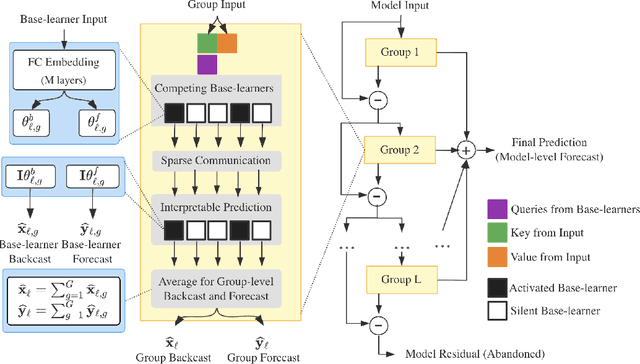
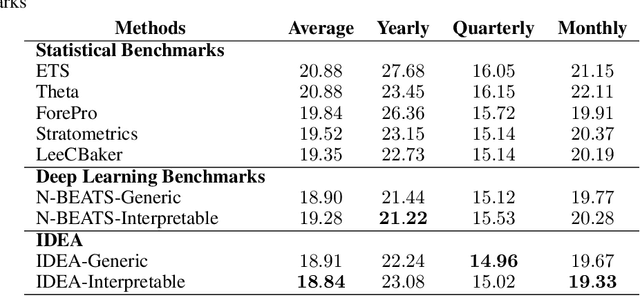
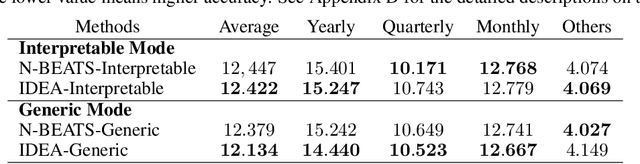
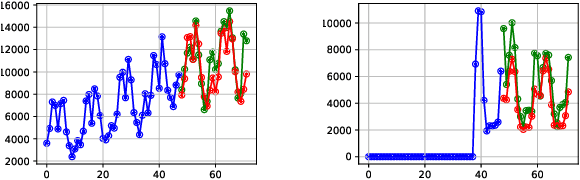
We enhance the accuracy and generalization of univariate time series point prediction by an explainable ensemble on the fly. We propose an Interpretable Dynamic Ensemble Architecture (IDEA), in which interpretable base learners give predictions independently with sparse communication as a group. The model is composed of several sequentially stacked groups connected by group backcast residuals and recurrent input competition. Ensemble driven by end-to-end training both horizontally and vertically brings state-of-the-art (SOTA) performances. Forecast accuracy improves by 2.6% over the best statistical benchmark on the TOURISM dataset and 2% over the best deep learning benchmark on the M4 dataset. The architecture enjoys several advantages, being applicable to time series from various domains, explainable to users with specialized modular structure and robust to changes in task distribution.

Time Series Generation with Masked Autoencoder

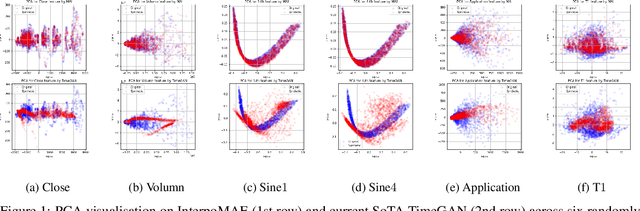
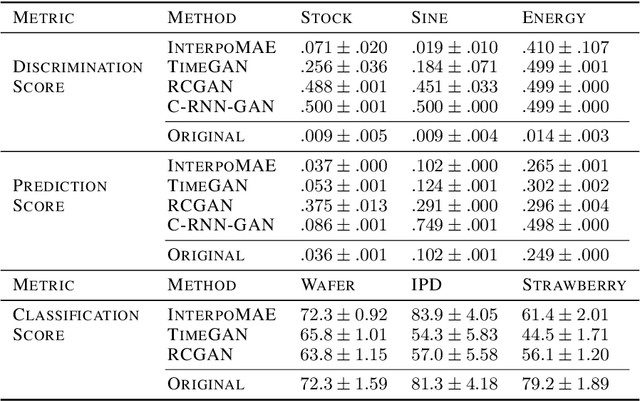
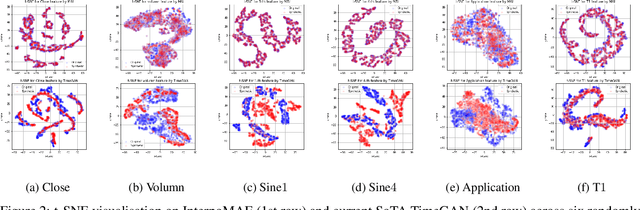
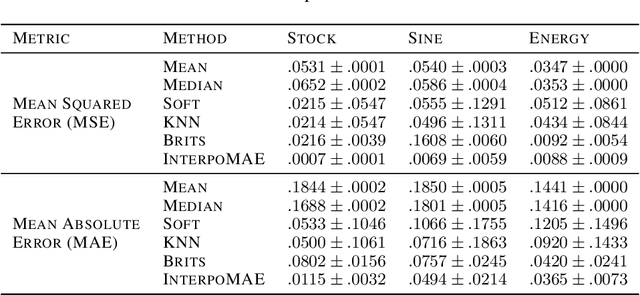
This paper shows that masked autoencoders with interpolators (InterpoMAE) are scalable self-supervised generators for time series. InterpoMAE masks random patches from the input time series and restore the missing patches in the latent space by an interpolator. The core design is that InterpoMAE uses an interpolator rather than mask tokens to restore the latent representations for missing patches in the latent space. This design enables more efficient and effective capture of temporal dynamics with bidirectional information. InterpoMAE allows for explicit control on the diversity of synthetic data by changing the size and number of masked patches. Our approach consistently and significantly outperforms state-of-the-art (SoTA) benchmarks of unsupervised learning in time series generation on several real datasets. Synthetic data produced show promising scaling behavior in various downstream tasks such as data augmentation, imputation and denoise.