Optimal Federated Learning for Nonparametric Regression with Heterogeneous Distributed Differential Privacy Constraints
Paper and Code
Jun 10, 2024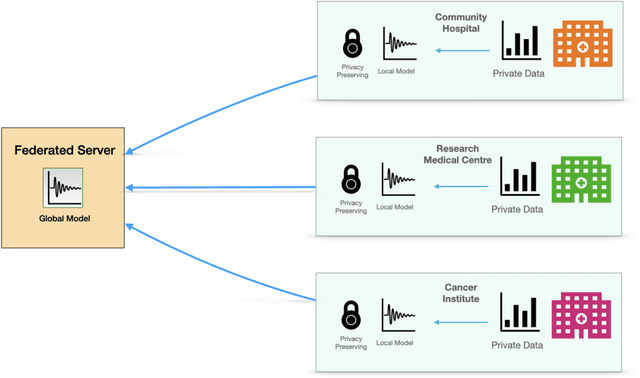
This paper studies federated learning for nonparametric regression in the context of distributed samples across different servers, each adhering to distinct differential privacy constraints. The setting we consider is heterogeneous, encompassing both varying sample sizes and differential privacy constraints across servers. Within this framework, both global and pointwise estimation are considered, and optimal rates of convergence over the Besov spaces are established. Distributed privacy-preserving estimators are proposed and their risk properties are investigated. Matching minimax lower bounds, up to a logarithmic factor, are established for both global and pointwise estimation. Together, these findings shed light on the tradeoff between statistical accuracy and privacy preservation. In particular, we characterize the compromise not only in terms of the privacy budget but also concerning the loss incurred by distributing data within the privacy framework as a whole. This insight captures the folklore wisdom that it is easier to retain privacy in larger samples, and explores the differences between pointwise and global estimation under distributed privacy constraints.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge