Huajun Xi
Robust Online Conformal Prediction under Uniform Label Noise
Jan 30, 2025Abstract:Conformal prediction is an emerging technique for uncertainty quantification that constructs prediction sets guaranteed to contain the true label with a predefined probability. Recent work develops online conformal prediction methods that adaptively construct prediction sets to accommodate distribution shifts. However, existing algorithms typically assume perfect label accuracy which rarely holds in practice. In this work, we investigate the robustness of online conformal prediction under uniform label noise with a known noise rate, in both constant and dynamic learning rate schedules. We show that label noise causes a persistent gap between the actual mis-coverage rate and the desired rate $\alpha$, leading to either overestimated or underestimated coverage guarantees. To address this issue, we propose Noise Robust Online Conformal Prediction (dubbed NR-OCP) by updating the threshold with a novel robust pinball los}, which provides an unbiased estimate of clean pinball loss without requiring ground-truth labels. Our theoretical analysis shows that NR-OCP eliminates the coverage gap in both constant and dynamic learning rate schedules, achieving a convergence rate of $\mathcal{O}(T^{-1/2})$ for both empirical and expected coverage errors under uniform label noise. Extensive experiments demonstrate the effectiveness of our method by achieving both precise coverage and improved efficiency.
Does Confidence Calibration Help Conformal Prediction?
Feb 06, 2024Abstract:Conformal prediction, as an emerging uncertainty qualification technique, constructs prediction sets that are guaranteed to contain the true label with high probability. Previous works usually employ temperature scaling to calibrate the classifier, assuming that confidence calibration can benefit conformal prediction. In this work, we first show that post-hoc calibration methods surprisingly lead to larger prediction sets with improved calibration, while over-confidence with small temperatures benefits the conformal prediction performance instead. Theoretically, we prove that high confidence reduces the probability of appending a new class in the prediction set. Inspired by the analysis, we propose a novel method, $\textbf{Conformal Temperature Scaling}$ (ConfTS), which rectifies the objective through the gap between the threshold and the non-conformity score of the ground-truth label. In this way, the new objective of ConfTS will optimize the temperature value toward an optimal set that satisfies the $\textit{marginal coverage}$. Experiments demonstrate that our method can effectively improve widely-used conformal prediction methods.
Conformal Prediction for Deep Classifier via Label Ranking
Oct 10, 2023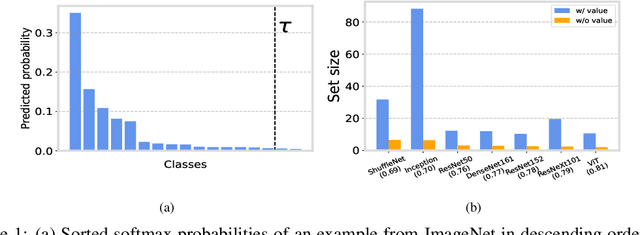
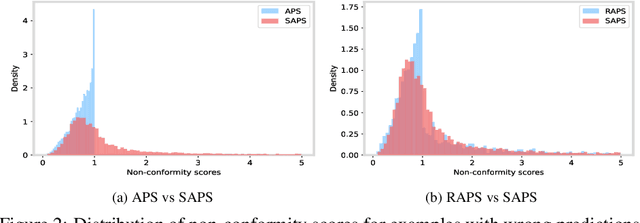
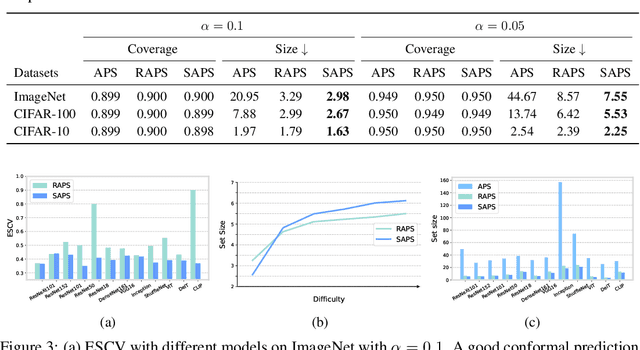
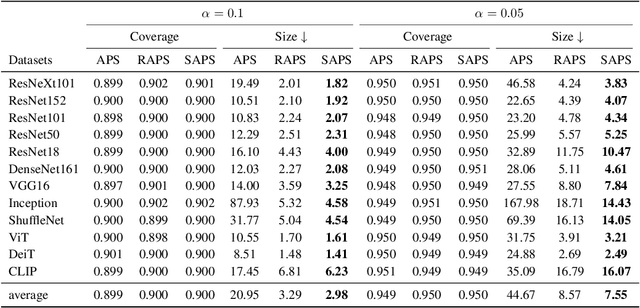
Abstract:Conformal prediction is a statistical framework that generates prediction sets containing ground-truth labels with a desired coverage guarantee. The predicted probabilities produced by machine learning models are generally miscalibrated, leading to large prediction sets in conformal prediction. In this paper, we empirically and theoretically show that disregarding the probabilities' value will mitigate the undesirable effect of miscalibrated probability values. Then, we propose a novel algorithm named $\textit{Sorted Adaptive prediction sets}$ (SAPS), which discards all the probability values except for the maximum softmax probability. The key idea behind SAPS is to minimize the dependence of the non-conformity score on the probability values while retaining the uncertainty information. In this manner, SAPS can produce sets of small size and communicate instance-wise uncertainty. Theoretically, we provide a finite-sample coverage guarantee of SAPS and show that the expected value of set size from SAPS is always smaller than APS. Extensive experiments validate that SAPS not only lessens the prediction sets but also broadly enhances the conditional coverage rate and adaptation of prediction sets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge