C-Adapter: Adapting Deep Classifiers for Efficient Conformal Prediction Sets

Conformal prediction, as an emerging uncertainty quantification technique, typically functions as post-hoc processing for the outputs of trained classifiers. To optimize the classifier for maximum predictive efficiency, Conformal Training rectifies the training objective with a regularization that minimizes the average prediction set size at a specific error rate. However, the regularization term inevitably deteriorates the classification accuracy and leads to suboptimal efficiency of conformal predictors. To address this issue, we introduce \textbf{Conformal Adapter} (C-Adapter), an adapter-based tuning method to enhance the efficiency of conformal predictors without sacrificing accuracy. In particular, we implement the adapter as a class of intra order-preserving functions and tune it with our proposed loss that maximizes the discriminability of non-conformity scores between correctly and randomly matched data-label pairs. Using C-Adapter, the model tends to produce extremely high non-conformity scores for incorrect labels, thereby enhancing the efficiency of prediction sets across different coverage rates. Extensive experiments demonstrate that C-Adapter can effectively adapt various classifiers for efficient prediction sets, as well as enhance the conformal training method.

IPEval: A Bilingual Intellectual Property Agency Consultation Evaluation Benchmark for Large Language Models

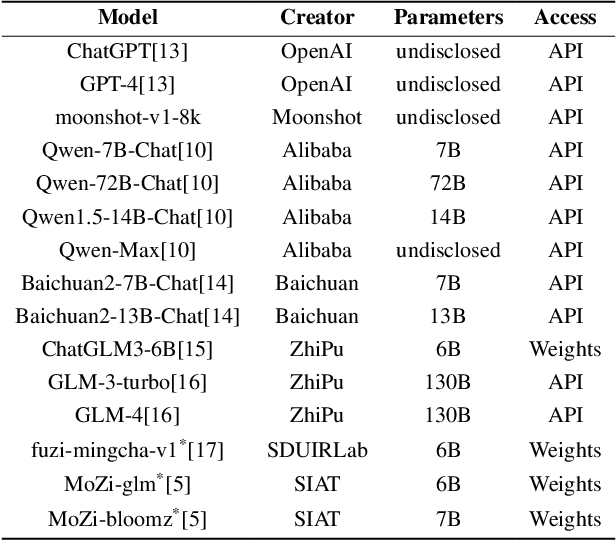
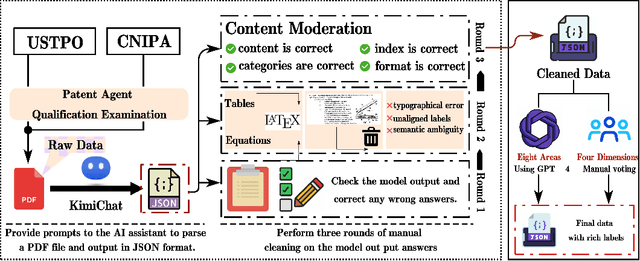
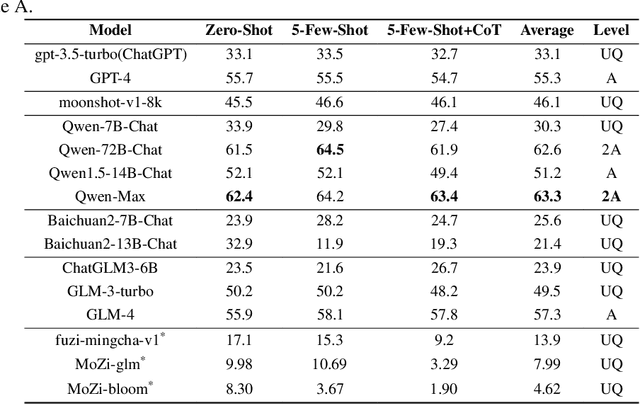
The rapid development of Large Language Models (LLMs) in vertical domains, including intellectual property (IP), lacks a specific evaluation benchmark for assessing their understanding, application, and reasoning abilities. To fill this gap, we introduce IPEval, the first evaluation benchmark tailored for IP agency and consulting tasks. IPEval comprises 2657 multiple-choice questions across four major dimensions: creation, application, protection, and management of IP. These questions span patent rights (inventions, utility models, designs), trademarks, copyrights, trade secrets, and other related laws. Evaluation methods include zero-shot, 5-few-shot, and Chain of Thought (CoT) for seven LLM types, predominantly in English or Chinese. Results show superior English performance by models like GPT series and Qwen series, while Chinese-centric LLMs excel in Chinese tests, albeit specialized IP LLMs lag behind general-purpose ones. Regional and temporal aspects of IP underscore the need for LLMs to grasp legal nuances and evolving laws. IPEval aims to accurately gauge LLM capabilities in IP and spur development of specialized models. Website: \url{https://ipeval.github.io/}

Similarity-Navigated Conformal Prediction for Graph Neural Networks

Graph Neural Networks have achieved remarkable accuracy in semi-supervised node classification tasks. However, these results lack reliable uncertainty estimates. Conformal prediction methods provide a theoretical guarantee for node classification tasks, ensuring that the conformal prediction set contains the ground-truth label with a desired probability (e.g., 95%). In this paper, we empirically show that for each node, aggregating the non-conformity scores of nodes with the same label can improve the efficiency of conformal prediction sets. This observation motivates us to propose a novel algorithm named Similarity-Navigated Adaptive Prediction Sets (SNAPS), which aggregates the non-conformity scores based on feature similarity and structural neighborhood. The key idea behind SNAPS is that nodes with high feature similarity or direct connections tend to have the same label. By incorporating adaptive similar nodes information, SNAPS can generate compact prediction sets and increase the singleton hit ratio (correct prediction sets of size one). Moreover, we theoretically provide a finite-sample coverage guarantee of SNAPS. Extensive experiments demonstrate the superiority of SNAPS, improving the efficiency of prediction sets and singleton hit ratio while maintaining valid coverage.

TorchCP: A Library for Conformal Prediction based on PyTorch

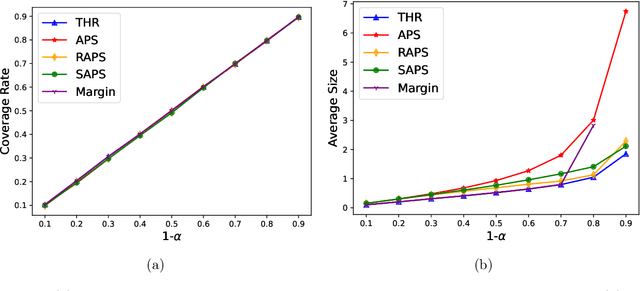
TorchCP is a Python toolbox for conformal prediction research on deep learning models. It contains various implementations for posthoc and training methods for classification and regression tasks (including multi-dimension output). TorchCP is built on PyTorch (Paszke et al., 2019) and leverages the advantages of matrix computation to provide concise and efficient inference implementations. The code is licensed under the LGPL license and is open-sourced at $\href{https://github.com/ml-stat-Sustech/TorchCP}{\text{this https URL}}$.

Does Confidence Calibration Help Conformal Prediction?

Conformal prediction, as an emerging uncertainty qualification technique, constructs prediction sets that are guaranteed to contain the true label with high probability. Previous works usually employ temperature scaling to calibrate the classifier, assuming that confidence calibration can benefit conformal prediction. In this work, we first show that post-hoc calibration methods surprisingly lead to larger prediction sets with improved calibration, while over-confidence with small temperatures benefits the conformal prediction performance instead. Theoretically, we prove that high confidence reduces the probability of appending a new class in the prediction set. Inspired by the analysis, we propose a novel method, $\textbf{Conformal Temperature Scaling}$ (ConfTS), which rectifies the objective through the gap between the threshold and the non-conformity score of the ground-truth label. In this way, the new objective of ConfTS will optimize the temperature value toward an optimal set that satisfies the $\textit{marginal coverage}$. Experiments demonstrate that our method can effectively improve widely-used conformal prediction methods.

Resolution invariant deep operator network for PDEs with complex geometries

Neural operators (NO) are discretization invariant deep learning methods with functional output and can approximate any continuous operator. NO have demonstrated the superiority of solving partial differential equations (PDEs) over other deep learning methods. However, the spatial domain of its input function needs to be identical to its output, which limits its applicability. For instance, the widely used Fourier neural operator (FNO) fails to approximate the operator that maps the boundary condition to the PDE solution. To address this issue, we propose a novel framework called resolution-invariant deep operator (RDO) that decouples the spatial domain of the input and output. RDO is motivated by the Deep operator network (DeepONet) and it does not require retraining the network when the input/output is changed compared with DeepONet. RDO takes functional input and its output is also functional so that it keeps the resolution invariant property of NO. It can also resolve PDEs with complex geometries whereas NO fail. Various numerical experiments demonstrate the advantage of our method over DeepONet and FNO.

Conformal Prediction for Deep Classifier via Label Ranking

Conformal prediction is a statistical framework that generates prediction sets containing ground-truth labels with a desired coverage guarantee. The predicted probabilities produced by machine learning models are generally miscalibrated, leading to large prediction sets in conformal prediction. In this paper, we empirically and theoretically show that disregarding the probabilities' value will mitigate the undesirable effect of miscalibrated probability values. Then, we propose a novel algorithm named $\textit{Sorted Adaptive prediction sets}$ (SAPS), which discards all the probability values except for the maximum softmax probability. The key idea behind SAPS is to minimize the dependence of the non-conformity score on the probability values while retaining the uncertainty information. In this manner, SAPS can produce sets of small size and communicate instance-wise uncertainty. Theoretically, we provide a finite-sample coverage guarantee of SAPS and show that the expected value of set size from SAPS is always smaller than APS. Extensive experiments validate that SAPS not only lessens the prediction sets but also broadly enhances the conditional coverage rate and adaptation of prediction sets.

Physics-informed invertible neural network for the Koopman operator learning

In Koopman operator theory, a finite-dimensional nonlinear system is transformed into an infinite but linear system using a set of observable functions. However, manually selecting observable functions that span the invariant subspace of the Koopman operator based on prior knowledge is inefficient and challenging, particularly when little or no information is available about the underlying systems. Furthermore, current methodologies tend to disregard the importance of the invertibility of observable functions, which leads to inaccurate results. To address these challenges, we propose the so-called FlowDMD, a Flow-based Dynamic Mode Decomposition that utilizes the Coupling Flow Invertible Neural Network (CF-INN) framework. FlowDMD leverages the intrinsically invertible characteristics of the CF-INN to learn the invariant subspaces of the Koopman operator and accurately reconstruct state variables. Numerical experiments demonstrate the superior performance of our algorithm compared to state-of-the-art methodologies.

Friedrichs Learning: Weak Solutions of Partial Differential Equations via Deep Learning

This paper proposes Friedrichs learning as a novel deep learning methodology that can learn the weak solutions of PDEs via a minmax formulation, which transforms the PDE problem into a minimax optimization problem to identify weak solutions. The name "Friedrichs learning" is for highlighting the close relationship between our learning strategy and Friedrichs theory on symmetric systems of PDEs. The weak solution and the test function in the weak formulation are parameterized as deep neural networks in a mesh-free manner, which are alternately updated to approach the optimal solution networks approximating the weak solution and the optimal test function, respectively. Extensive numerical results indicate that our mesh-free method can provide reasonably good solutions to a wide range of PDEs defined on regular and irregular domains in various dimensions, where classical numerical methods such as finite difference methods and finite element methods may be tedious or difficult to be applied.

Online dictionary learning for kernel LMS. Analysis and forward-backward splitting algorithm

Adaptive filtering algorithms operating in reproducing kernel Hilbert spaces have demonstrated superiority over their linear counterpart for nonlinear system identification. Unfortunately, an undesirable characteristic of these methods is that the order of the filters grows linearly with the number of input data. This dramatically increases the computational burden and memory requirement. A variety of strategies based on dictionary learning have been proposed to overcome this severe drawback. Few, if any, of these works analyze the problem of updating the dictionary in a time-varying environment. In this paper, we present an analytical study of the convergence behavior of the Gaussian least-mean-square algorithm in the case where the statistics of the dictionary elements only partially match the statistics of the input data. This allows us to emphasize the need for updating the dictionary in an online way, by discarding the obsolete elements and adding appropriate ones. We introduce a kernel least-mean-square algorithm with L1-norm regularization to automatically perform this task. The stability in the mean of this method is analyzed, and its performance is tested with experiments.