H-FEX: A Symbolic Learning Method for Hamiltonian Systems

Hamiltonian systems describe a broad class of dynamical systems governed by Hamiltonian functions, which encode the total energy and dictate the evolution of the system. Data-driven approaches, such as symbolic regression and neural network-based methods, provide a means to learn the governing equations of dynamical systems directly from observational data of Hamiltonian systems. However, these methods often struggle to accurately capture complex Hamiltonian functions while preserving energy conservation. To overcome this limitation, we propose the Finite Expression Method for learning Hamiltonian Systems (H-FEX), a symbolic learning method that introduces novel interaction nodes designed to capture intricate interaction terms effectively. Our experiments, including those on highly stiff dynamical systems, demonstrate that H-FEX can recover Hamiltonian functions of complex systems that accurately capture system dynamics and preserve energy over long time horizons. These findings highlight the potential of H-FEX as a powerful framework for discovering closed-form expressions of complex dynamical systems.

Identifying Unknown Stochastic Dynamics via Finite expression methods

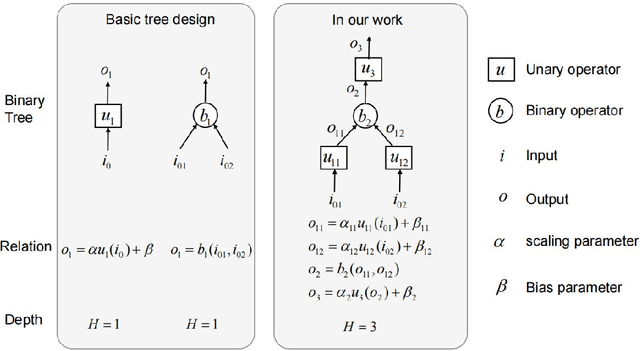
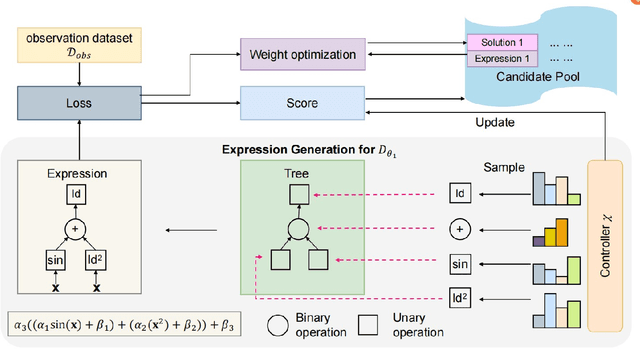
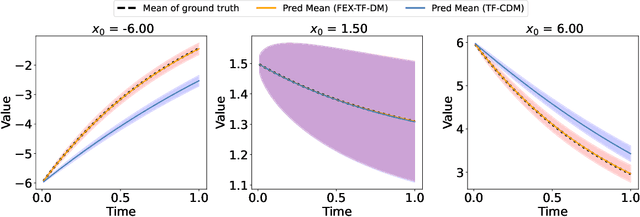
Modeling stochastic differential equations (SDEs) is crucial for understanding complex dynamical systems in various scientific fields. Recent methods often employ neural network-based models, which typically represent SDEs through a combination of deterministic and stochastic terms. However, these models usually lack interpretability and have difficulty generalizing beyond their training domain. This paper introduces the Finite Expression Method (FEX), a symbolic learning approach designed to derive interpretable mathematical representations of the deterministic component of SDEs. For the stochastic component, we integrate FEX with advanced generative modeling techniques to provide a comprehensive representation of SDEs. The numerical experiments on linear, nonlinear, and multidimensional SDEs demonstrate that FEX generalizes well beyond the training domain and delivers more accurate long-term predictions compared to neural network-based methods. The symbolic expressions identified by FEX not only improve prediction accuracy but also offer valuable scientific insights into the underlying dynamics of the systems, paving the way for new scientific discoveries.

Learning Epidemiological Dynamics via the Finite Expression Method

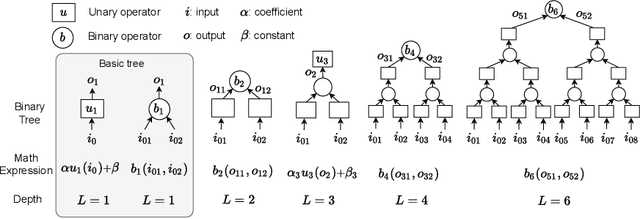
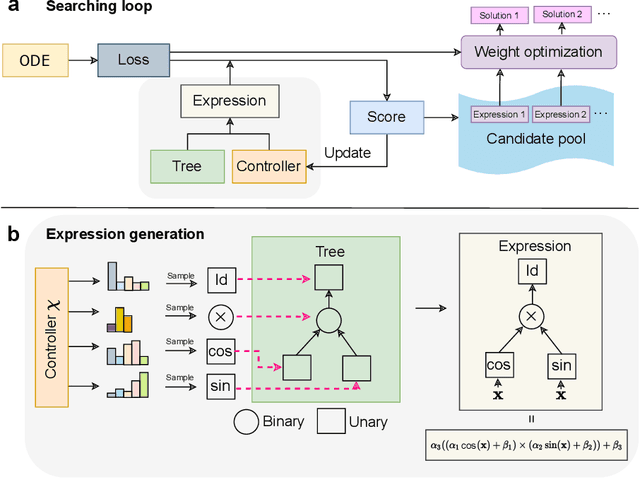
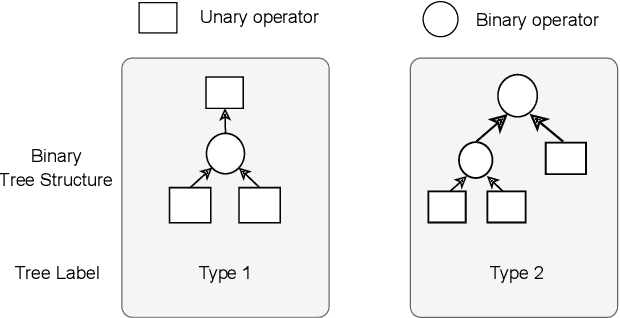
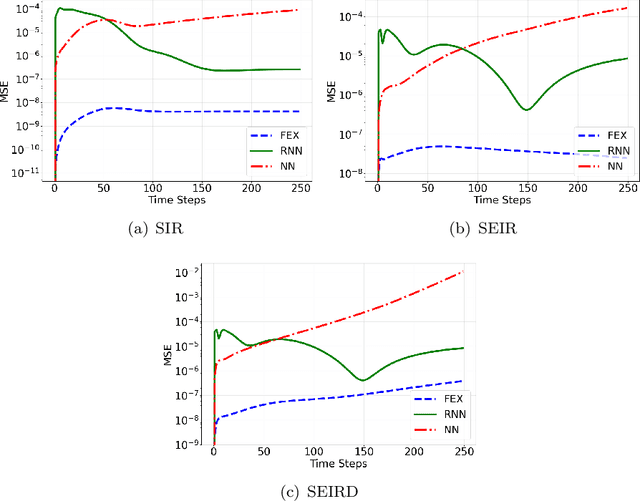
Modeling and forecasting the spread of infectious diseases is essential for effective public health decision-making. Traditional epidemiological models rely on expert-defined frameworks to describe complex dynamics, while neural networks, despite their predictive power, often lack interpretability due to their ``black-box" nature. This paper introduces the Finite Expression Method, a symbolic learning framework that leverages reinforcement learning to derive explicit mathematical expressions for epidemiological dynamics. Through numerical experiments on both synthetic and real-world datasets, FEX demonstrates high accuracy in modeling and predicting disease spread, while uncovering explicit relationships among epidemiological variables. These results highlight FEX as a powerful tool for infectious disease modeling, combining interpretability with strong predictive performance to support practical applications in public health.

Finite Expression Methods for Discovering Physical Laws from Data

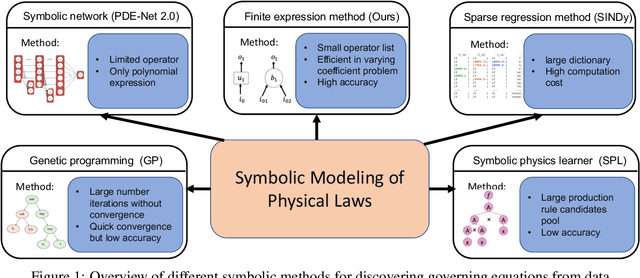
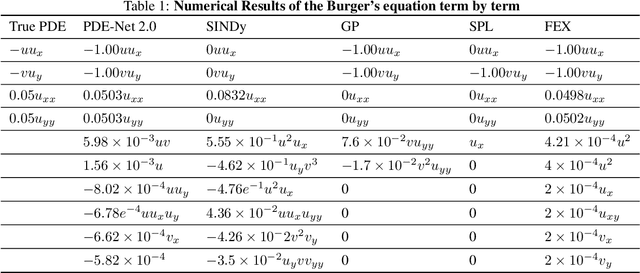
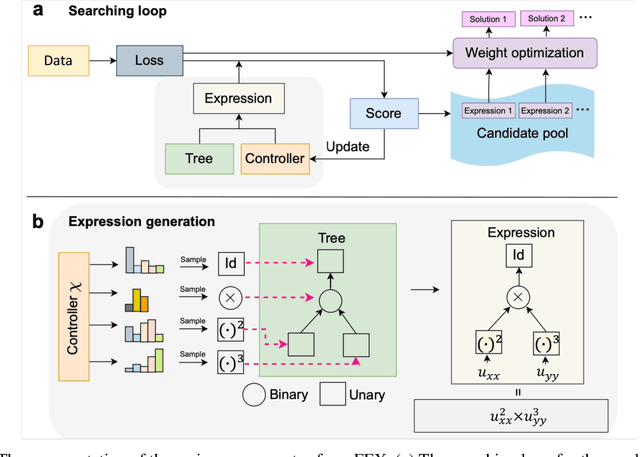
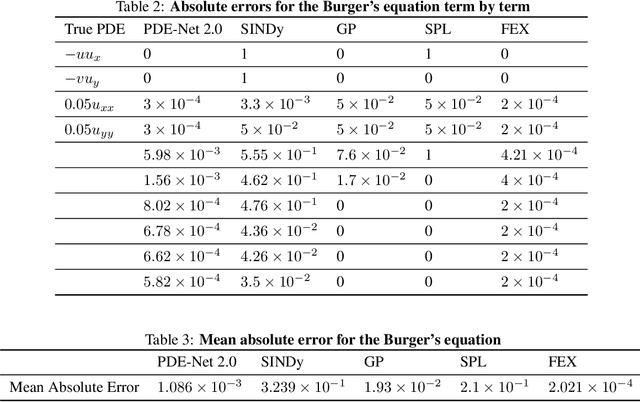
Nonlinear dynamics is a pervasive phenomenon observed in various scientific and engineering disciplines. However, uncovering analytical expressions that describe nonlinear dynamics from limited data remains a challenging and essential task. In this paper, we propose a new deep symbolic learning method called the ``finite expression method'' (FEX) to identify the governing equations within the space of functions containing a finite set of analytic expressions, based on observed dynamic data. The core idea is to leverage FEX to generate analytical expressions of the governing equations by learning the derivatives of partial differential equation (PDE) solutions using convolutions. Our numerical results demonstrate that FEX outperforms all existing methods (such as PDE-Net, SINDy, GP, and SPL) in terms of numerical performance across various problems, including time-dependent PDE problems and nonlinear dynamical systems with time-varying coefficients. Furthermore, the results highlight that FEX exhibits flexibility and expressive power in accurately approximating symbolic governing equations, while maintaining low memory and favorable time complexity.

Deep Operator Learning Lessens the Curse of Dimensionality for PDEs

Deep neural networks (DNNs) have seen tremendous success in many fields and their developments in PDE-related problems are rapidly growing. This paper provides an estimate for the generalization error of learning Lipschitz operators over Banach spaces using DNNs with applications to various PDE solution operators. The goal is to specify DNN width, depth, and the number of training samples needed to guarantee a certain testing error. Under mild assumptions on data distributions or operator structures, our analysis shows that deep operator learning can have a relaxed dependence on the discretization resolution of PDEs and, hence, lessen the curse of dimensionality in many PDE-related problems. We apply our results to various PDEs, including elliptic equations, parabolic equations, and Burgers equations.

Friedrichs Learning: Weak Solutions of Partial Differential Equations via Deep Learning

This paper proposes Friedrichs learning as a novel deep learning methodology that can learn the weak solutions of PDEs via a minmax formulation, which transforms the PDE problem into a minimax optimization problem to identify weak solutions. The name "Friedrichs learning" is for highlighting the close relationship between our learning strategy and Friedrichs theory on symmetric systems of PDEs. The weak solution and the test function in the weak formulation are parameterized as deep neural networks in a mesh-free manner, which are alternately updated to approach the optimal solution networks approximating the weak solution and the optimal test function, respectively. Extensive numerical results indicate that our mesh-free method can provide reasonably good solutions to a wide range of PDEs defined on regular and irregular domains in various dimensions, where classical numerical methods such as finite difference methods and finite element methods may be tedious or difficult to be applied.

Reproducing Activation Function for Deep Learning

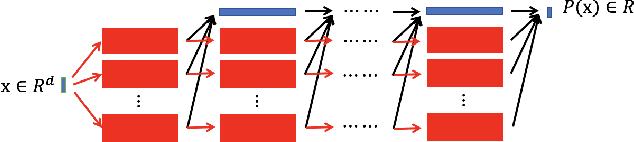
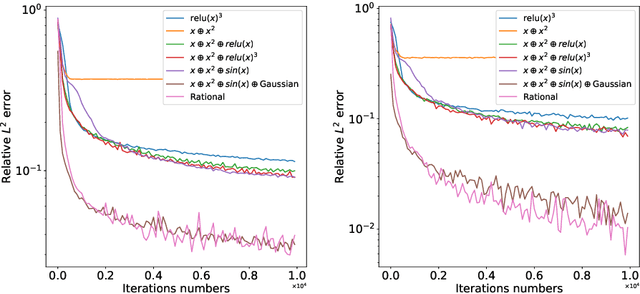
In this paper, we propose the reproducing activation function to improve deep learning accuracy for various applications ranging from computer vision problems to scientific computing problems. The idea of reproducing activation functions is to employ several basic functions and their learnable linear combination to construct neuron-wise data-driven activation functions for each neuron. Armed with such activation functions, deep neural networks can reproduce traditional approximation tools and, therefore, approximate target functions with a smaller number of parameters than traditional neural networks. In terms of training dynamics of deep learning, reproducing activation functions can generate neural tangent kernels with a better condition number than traditional activation functions lessening the spectral bias of deep learning. As demonstrated by extensive numerical tests, the proposed activation function can facilitate the convergence of deep learning optimization for a solution with higher accuracy than existing deep learning solvers for audio/image/video reconstruction, PDEs, and eigenvalue problems.