Finite Expression Methods for Discovering Physical Laws from Data

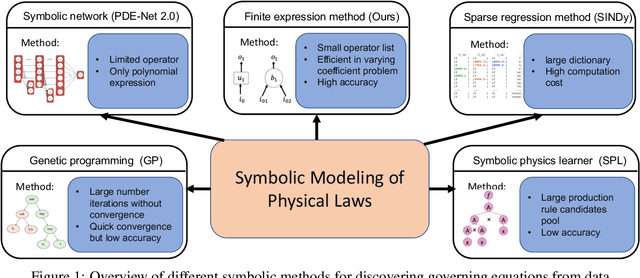
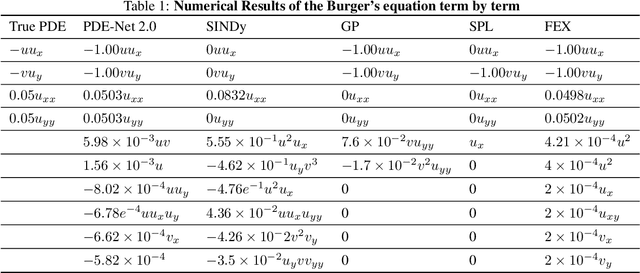
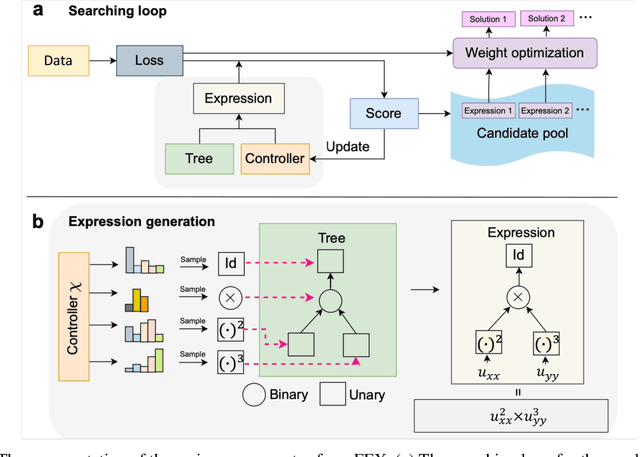
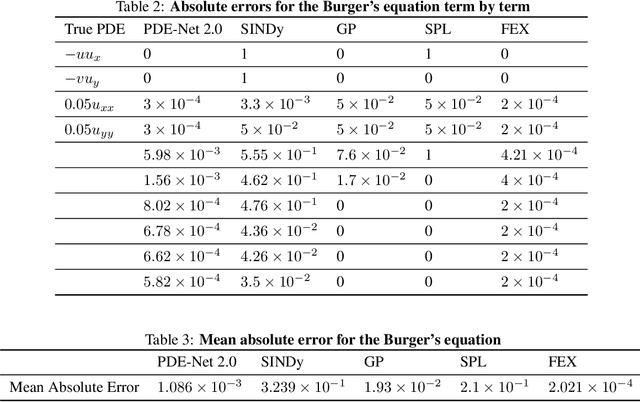
Nonlinear dynamics is a pervasive phenomenon observed in various scientific and engineering disciplines. However, uncovering analytical expressions that describe nonlinear dynamics from limited data remains a challenging and essential task. In this paper, we propose a new deep symbolic learning method called the ``finite expression method'' (FEX) to identify the governing equations within the space of functions containing a finite set of analytic expressions, based on observed dynamic data. The core idea is to leverage FEX to generate analytical expressions of the governing equations by learning the derivatives of partial differential equation (PDE) solutions using convolutions. Our numerical results demonstrate that FEX outperforms all existing methods (such as PDE-Net, SINDy, GP, and SPL) in terms of numerical performance across various problems, including time-dependent PDE problems and nonlinear dynamical systems with time-varying coefficients. Furthermore, the results highlight that FEX exhibits flexibility and expressive power in accurately approximating symbolic governing equations, while maintaining low memory and favorable time complexity.