Finite Expression Methods for Discovering Physical Laws from Data

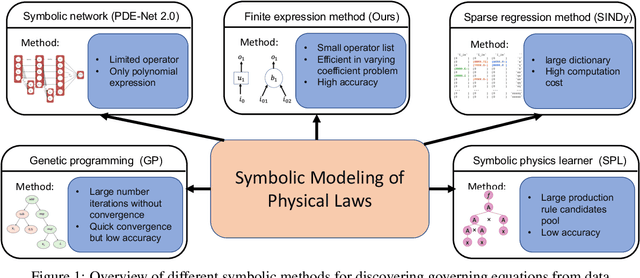
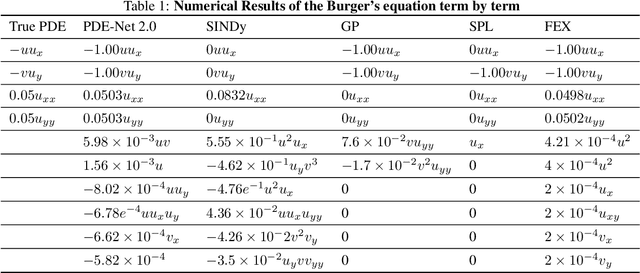
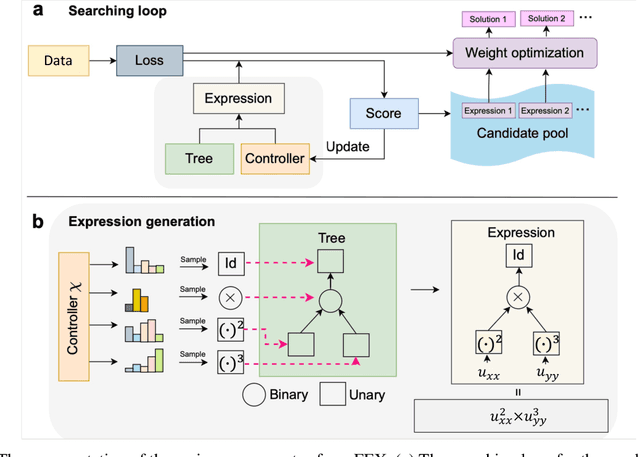
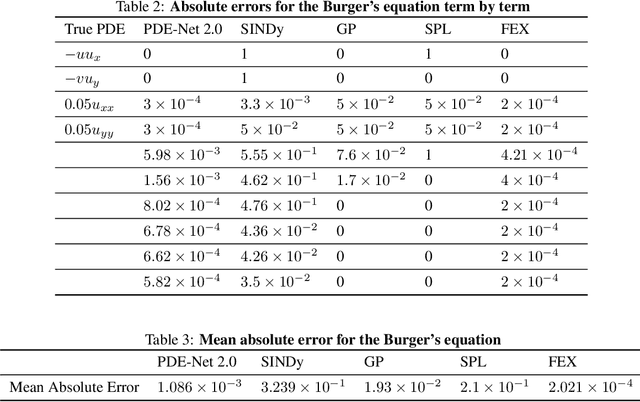
Nonlinear dynamics is a pervasive phenomenon observed in various scientific and engineering disciplines. However, uncovering analytical expressions that describe nonlinear dynamics from limited data remains a challenging and essential task. In this paper, we propose a new deep symbolic learning method called the ``finite expression method'' (FEX) to identify the governing equations within the space of functions containing a finite set of analytic expressions, based on observed dynamic data. The core idea is to leverage FEX to generate analytical expressions of the governing equations by learning the derivatives of partial differential equation (PDE) solutions using convolutions. Our numerical results demonstrate that FEX outperforms all existing methods (such as PDE-Net, SINDy, GP, and SPL) in terms of numerical performance across various problems, including time-dependent PDE problems and nonlinear dynamical systems with time-varying coefficients. Furthermore, the results highlight that FEX exhibits flexibility and expressive power in accurately approximating symbolic governing equations, while maintaining low memory and favorable time complexity.

Fourier-MIONet: Fourier-enhanced multiple-input neural operators for multiphase modeling of geological carbon sequestration

Geologic Carbon Storage (GCS) is an important technology that aims to reduce the amount of carbon dioxide in the atmosphere. Multiphase flow in porous media is essential to understand CO2 migration and pressure fields in the subsurface associated with GCS. However, numerical simulation for such problems in 4D is computationally challenging and expensive, due to the multiphysics and multiscale nature of the highly nonlinear governing partial differential equations (PDEs). It prevents us from considering multiple subsurface scenarios and conducting real-time optimization. Here, we develop a Fourier-enhanced multiple-input neural operator (Fourier-MIONet) to learn the solution operator of the problem of multiphase flow in porous media. Fourier-MIONet utilizes the recently developed framework of the multiple-input deep neural operators (MIONet) and incorporates the Fourier neural operator (FNO) in the network architecture. Once Fourier-MIONet is trained, it can predict the evolution of saturation and pressure of the multiphase flow under various reservoir conditions, such as permeability and porosity heterogeneity, anisotropy, injection configurations, and multiphase flow properties. Compared to the enhanced FNO (U-FNO), the proposed Fourier-MIONet has 90% fewer unknown parameters, and it can be trained in significantly less time (about 3.5 times faster) with much lower CPU memory (< 15%) and GPU memory (< 35%) requirements, to achieve similar prediction accuracy. In addition to the lower computational cost, Fourier-MIONet can be trained with only 6 snapshots of time to predict the PDE solutions for 30 years. The excellent generalizability of Fourier-MIONet is enabled by its adherence to the physical principle that the solution to a PDE is continuous over time.

MAF-GNN: Multi-adaptive Spatiotemporal-flow Graph Neural Network for Traffic Speed Forecasting

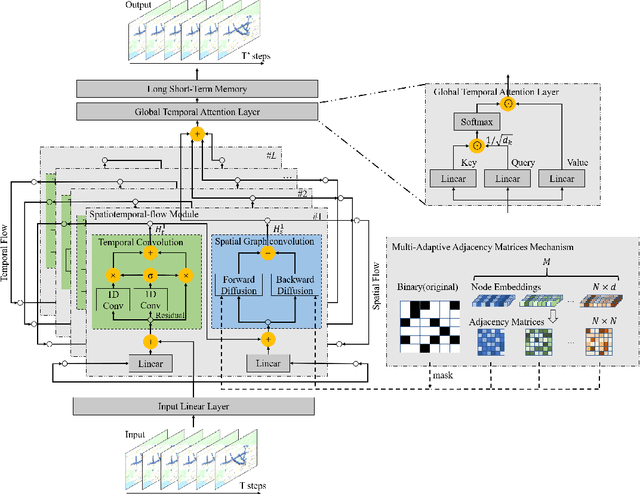
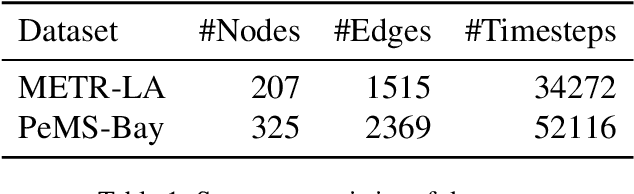
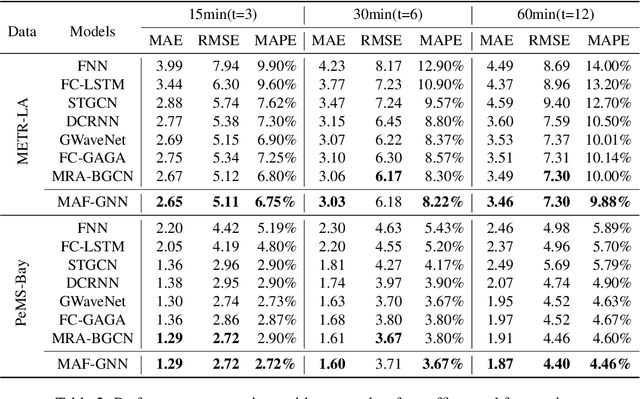
Traffic forecasting is a core element of intelligent traffic monitoring system. Approaches based on graph neural networks have been widely used in this task to effectively capture spatial and temporal dependencies of road networks. However, these approaches can not effectively define the complicated network topology. Besides, their cascade network structures have limitations in transmitting distinct features in the time and space dimensions. In this paper, we propose a Multi-adaptive Spatiotemporal-flow Graph Neural Network (MAF-GNN) for traffic speed forecasting. MAF-GNN introduces an effective Multi-adaptive Adjacency Matrices Mechanism to capture multiple latent spatial dependencies between traffic nodes. Additionally, we propose Spatiotemporal-flow Modules aiming to further enhance feature propagation in both time and space dimensions. MAF-GNN achieves better performance than other models on two real-world datasets of public traffic network, METR-LA and PeMS-Bay, demonstrating the effectiveness of the proposed approach.