Efficient and generalizable nested Fourier-DeepONet for three-dimensional geological carbon sequestration

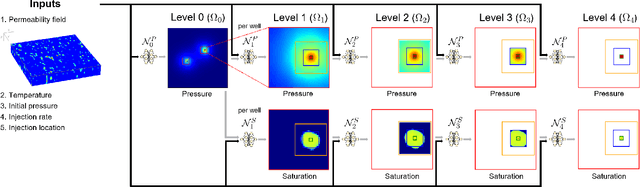
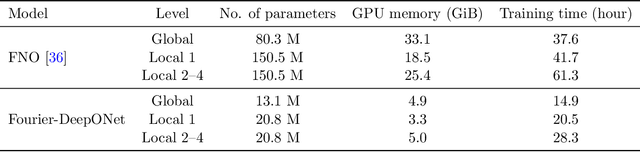
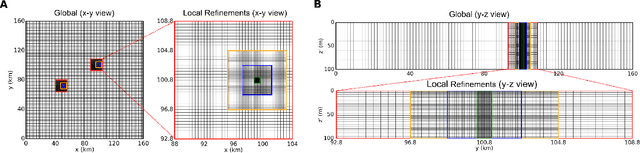
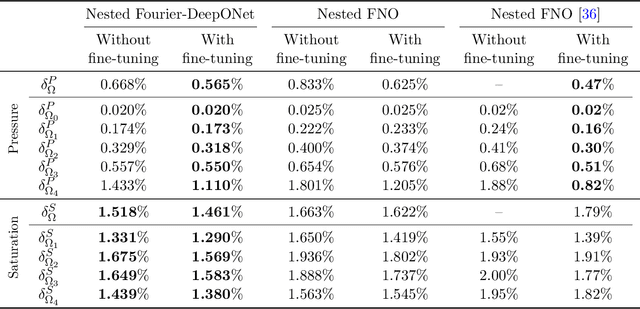
Geological carbon sequestration (GCS) involves injecting CO$_2$ into subsurface geological formations for permanent storage. Numerical simulations could guide decisions in GCS projects by predicting CO$_2$ migration pathways and the pressure distribution in storage formation. However, these simulations are often computationally expensive due to highly coupled physics and large spatial-temporal simulation domains. Surrogate modeling with data-driven machine learning has become a promising alternative to accelerate physics-based simulations. Among these, the Fourier neural operator (FNO) has been applied to three-dimensional synthetic subsurface models. Here, to further improve performance, we have developed a nested Fourier-DeepONet by combining the expressiveness of the FNO with the modularity of a deep operator network (DeepONet). This new framework is twice as efficient as a nested FNO for training and has at least 80% lower GPU memory requirement due to its flexibility to treat temporal coordinates separately. These performance improvements are achieved without compromising prediction accuracy. In addition, the generalization and extrapolation ability of nested Fourier-DeepONet beyond the training range has been thoroughly evaluated. Nested Fourier-DeepONet outperformed the nested FNO for extrapolation in time with more than 50% reduced error. It also exhibited good extrapolation accuracy beyond the training range in terms of reservoir properties, number of wells, and injection rate.

Fourier-MIONet: Fourier-enhanced multiple-input neural operators for multiphase modeling of geological carbon sequestration

Geologic Carbon Storage (GCS) is an important technology that aims to reduce the amount of carbon dioxide in the atmosphere. Multiphase flow in porous media is essential to understand CO2 migration and pressure fields in the subsurface associated with GCS. However, numerical simulation for such problems in 4D is computationally challenging and expensive, due to the multiphysics and multiscale nature of the highly nonlinear governing partial differential equations (PDEs). It prevents us from considering multiple subsurface scenarios and conducting real-time optimization. Here, we develop a Fourier-enhanced multiple-input neural operator (Fourier-MIONet) to learn the solution operator of the problem of multiphase flow in porous media. Fourier-MIONet utilizes the recently developed framework of the multiple-input deep neural operators (MIONet) and incorporates the Fourier neural operator (FNO) in the network architecture. Once Fourier-MIONet is trained, it can predict the evolution of saturation and pressure of the multiphase flow under various reservoir conditions, such as permeability and porosity heterogeneity, anisotropy, injection configurations, and multiphase flow properties. Compared to the enhanced FNO (U-FNO), the proposed Fourier-MIONet has 90% fewer unknown parameters, and it can be trained in significantly less time (about 3.5 times faster) with much lower CPU memory (< 15%) and GPU memory (< 35%) requirements, to achieve similar prediction accuracy. In addition to the lower computational cost, Fourier-MIONet can be trained with only 6 snapshots of time to predict the PDE solutions for 30 years. The excellent generalizability of Fourier-MIONet is enabled by its adherence to the physical principle that the solution to a PDE is continuous over time.