H-FEX: A Symbolic Learning Method for Hamiltonian Systems

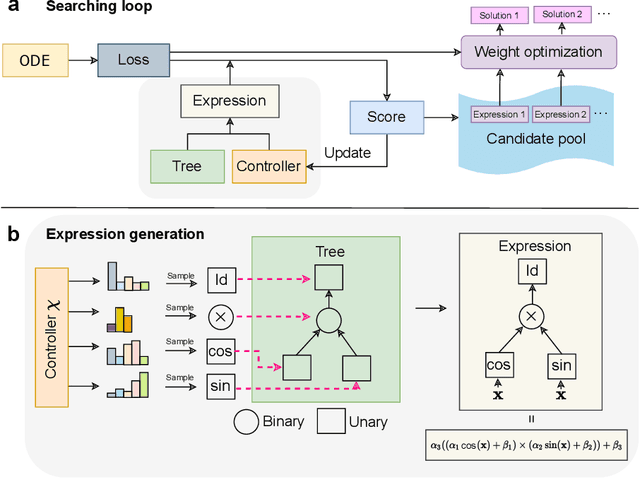
Hamiltonian systems describe a broad class of dynamical systems governed by Hamiltonian functions, which encode the total energy and dictate the evolution of the system. Data-driven approaches, such as symbolic regression and neural network-based methods, provide a means to learn the governing equations of dynamical systems directly from observational data of Hamiltonian systems. However, these methods often struggle to accurately capture complex Hamiltonian functions while preserving energy conservation. To overcome this limitation, we propose the Finite Expression Method for learning Hamiltonian Systems (H-FEX), a symbolic learning method that introduces novel interaction nodes designed to capture intricate interaction terms effectively. Our experiments, including those on highly stiff dynamical systems, demonstrate that H-FEX can recover Hamiltonian functions of complex systems that accurately capture system dynamics and preserve energy over long time horizons. These findings highlight the potential of H-FEX as a powerful framework for discovering closed-form expressions of complex dynamical systems.

Identifying Unknown Stochastic Dynamics via Finite expression methods

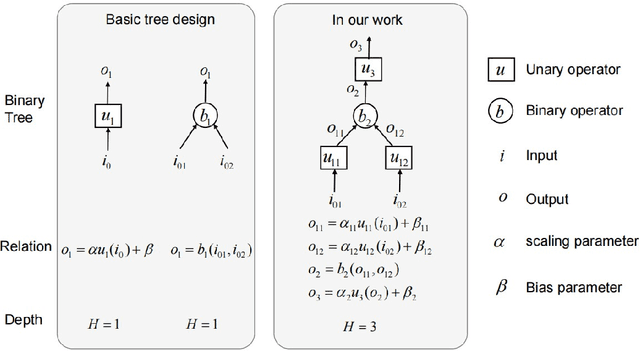
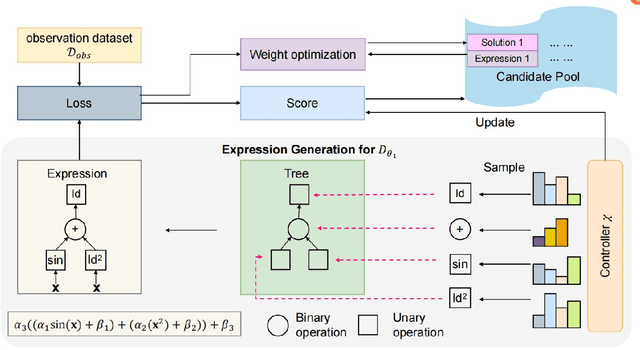
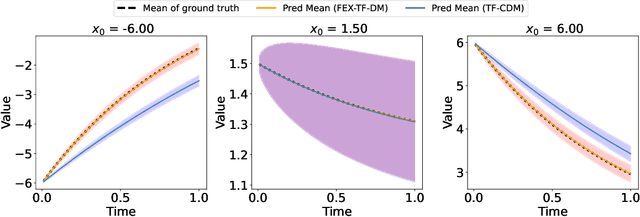
Modeling stochastic differential equations (SDEs) is crucial for understanding complex dynamical systems in various scientific fields. Recent methods often employ neural network-based models, which typically represent SDEs through a combination of deterministic and stochastic terms. However, these models usually lack interpretability and have difficulty generalizing beyond their training domain. This paper introduces the Finite Expression Method (FEX), a symbolic learning approach designed to derive interpretable mathematical representations of the deterministic component of SDEs. For the stochastic component, we integrate FEX with advanced generative modeling techniques to provide a comprehensive representation of SDEs. The numerical experiments on linear, nonlinear, and multidimensional SDEs demonstrate that FEX generalizes well beyond the training domain and delivers more accurate long-term predictions compared to neural network-based methods. The symbolic expressions identified by FEX not only improve prediction accuracy but also offer valuable scientific insights into the underlying dynamics of the systems, paving the way for new scientific discoveries.

Robust Multimodal Learning for Ophthalmic Disease Grading via Disentangled Representation

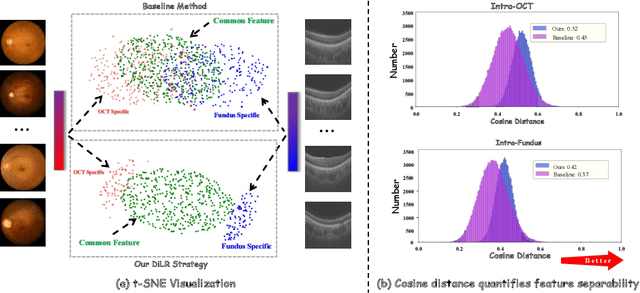
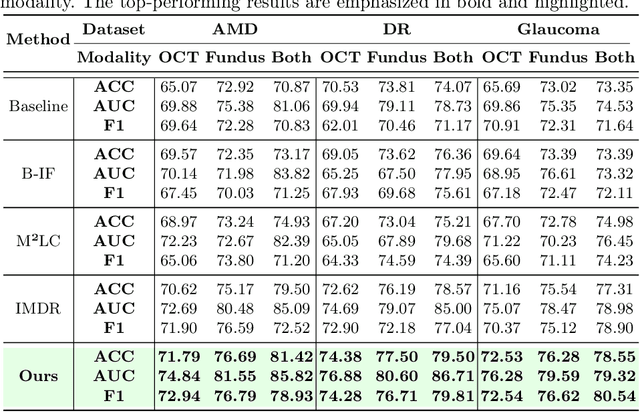
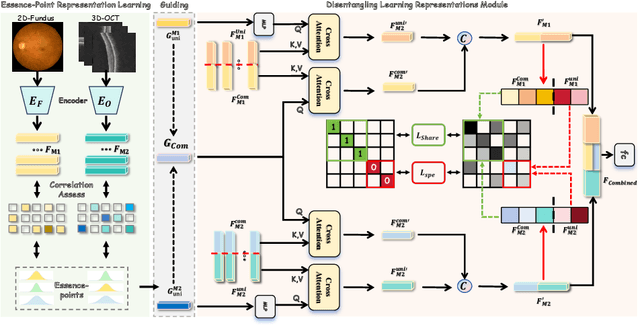
This paper discusses how ophthalmologists often rely on multimodal data to improve diagnostic accuracy. However, complete multimodal data is rare in real-world applications due to a lack of medical equipment and concerns about data privacy. Traditional deep learning methods typically address these issues by learning representations in latent space. However, the paper highlights two key limitations of these approaches: (i) Task-irrelevant redundant information (e.g., numerous slices) in complex modalities leads to significant redundancy in latent space representations. (ii) Overlapping multimodal representations make it difficult to extract unique features for each modality. To overcome these challenges, the authors propose the Essence-Point and Disentangle Representation Learning (EDRL) strategy, which integrates a self-distillation mechanism into an end-to-end framework to enhance feature selection and disentanglement for more robust multimodal learning. Specifically, the Essence-Point Representation Learning module selects discriminative features that improve disease grading performance. The Disentangled Representation Learning module separates multimodal data into modality-common and modality-unique representations, reducing feature entanglement and enhancing both robustness and interpretability in ophthalmic disease diagnosis. Experiments on multimodal ophthalmology datasets show that the proposed EDRL strategy significantly outperforms current state-of-the-art methods.

Learning Epidemiological Dynamics via the Finite Expression Method

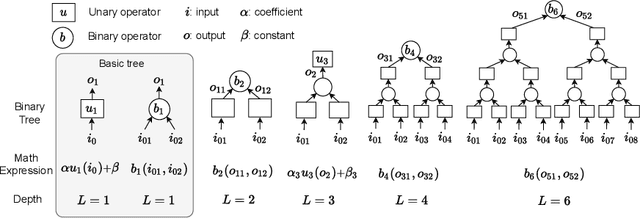
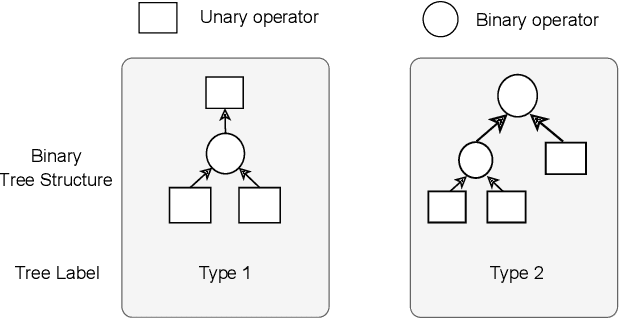
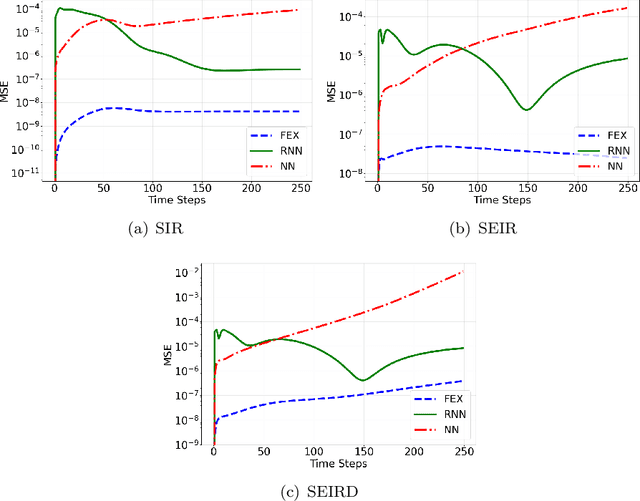
Modeling and forecasting the spread of infectious diseases is essential for effective public health decision-making. Traditional epidemiological models rely on expert-defined frameworks to describe complex dynamics, while neural networks, despite their predictive power, often lack interpretability due to their ``black-box" nature. This paper introduces the Finite Expression Method, a symbolic learning framework that leverages reinforcement learning to derive explicit mathematical expressions for epidemiological dynamics. Through numerical experiments on both synthetic and real-world datasets, FEX demonstrates high accuracy in modeling and predicting disease spread, while uncovering explicit relationships among epidemiological variables. These results highlight FEX as a powerful tool for infectious disease modeling, combining interpretability with strong predictive performance to support practical applications in public health.

Solving High-Dimensional Partial Integral Differential Equations: The Finite Expression Method

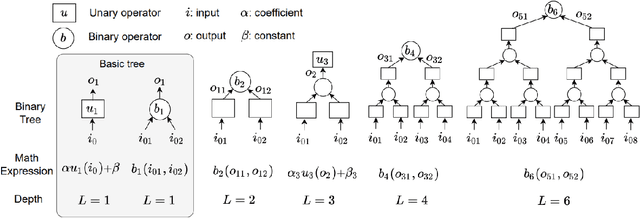
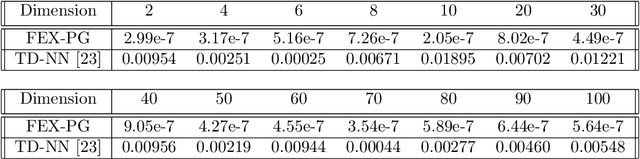
In this paper, we introduce a new finite expression method (FEX) to solve high-dimensional partial integro-differential equations (PIDEs). This approach builds upon the original FEX and its inherent advantages with new advances: 1) A novel method of parameter grouping is proposed to reduce the number of coefficients in high-dimensional function approximation; 2) A Taylor series approximation method is implemented to significantly improve the computational efficiency and accuracy of the evaluation of the integral terms of PIDEs. The new FEX based method, denoted FEX-PG to indicate the addition of the parameter grouping (PG) step to the algorithm, provides both high accuracy and interpretable numerical solutions, with the outcome being an explicit equation that facilitates intuitive understanding of the underlying solution structures. These features are often absent in traditional methods, such as finite element methods (FEM) and finite difference methods, as well as in deep learning-based approaches. To benchmark our method against recent advances, we apply the new FEX-PG to solve benchmark PIDEs in the literature. In high-dimensional settings, FEX-PG exhibits strong and robust performance, achieving relative errors on the order of single precision machine epsilon.

Learning nonlinear integral operators via Recurrent Neural Networks and its application in solving Integro-Differential Equations

In this paper, we propose using LSTM-RNNs (Long Short-Term Memory-Recurrent Neural Networks) to learn and represent nonlinear integral operators that appear in nonlinear integro-differential equations (IDEs). The LSTM-RNN representation of the nonlinear integral operator allows us to turn a system of nonlinear integro-differential equations into a system of ordinary differential equations for which many efficient solvers are available. Furthermore, because the use of LSTM-RNN representation of the nonlinear integral operator in an IDE eliminates the need to perform a numerical integration in each numerical time evolution step, the overall temporal cost of the LSTM-RNN-based IDE solver can be reduced to $O(n_T)$ from $O(n_T^2)$ if a $n_T$-step trajectory is to be computed. We illustrate the efficiency and robustness of this LSTM-RNN-based numerical IDE solver with a model problem. Additionally, we highlight the generalizability of the learned integral operator by applying it to IDEs driven by different external forces. As a practical application, we show how this methodology can effectively solve the Dyson's equation for quantum many-body systems.

Probing reaction channels via reinforcement learning

We propose a reinforcement learning based method to identify important configurations that connect reactant and product states along chemical reaction paths. By shooting multiple trajectories from these configurations, we can generate an ensemble of configurations that concentrate on the transition path ensemble. This configuration ensemble can be effectively employed in a neural network-based partial differential equation solver to obtain an approximation solution of a restricted Backward Kolmogorov equation, even when the dimension of the problem is very high. The resulting solution, known as the committor function, encodes mechanistic information for the reaction and can in turn be used to evaluate reaction rates.

Layer-wise Shared Attention Network on Dynamical System Perspective

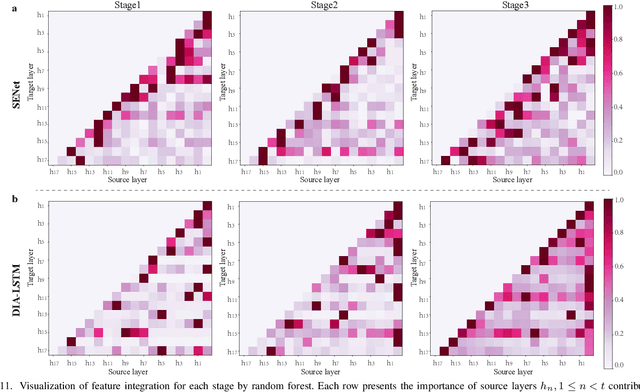
Attention networks have successfully boosted accuracy in various vision problems. Previous works lay emphasis on designing a new self-attention module and follow the traditional paradigm that individually plugs the modules into each layer of a network. However, such a paradigm inevitably increases the extra parameter cost with the growth of the number of layers. From the dynamical system perspective of the residual neural network, we find that the feature maps from the layers of the same stage are homogenous, which inspires us to propose a novel-and-simple framework, called the dense and implicit attention (DIA) unit, that shares a single attention module throughout different network layers. With our framework, the parameter cost is independent of the number of layers and we further improve the accuracy of existing popular self-attention modules with significant parameter reduction without any elaborated model crafting. Extensive experiments on benchmark datasets show that the DIA is capable of emphasizing layer-wise feature interrelation and thus leads to significant improvement in various vision tasks, including image classification, object detection, and medical application. Furthermore, the effectiveness of the DIA unit is demonstrated by novel experiments where we destabilize the model training by (1) removing the skip connection of the residual neural network, (2) removing the batch normalization of the model, and (3) removing all data augmentation during training. In these cases, we verify that DIA has a strong regularization ability to stabilize the training, i.e., the dense and implicit connections formed by our method can effectively recover and enhance the information communication across layers and the value of the gradient thus alleviate the training instability.

Accelerating Numerical Solvers for Large-Scale Simulation of Dynamical System via NeurVec

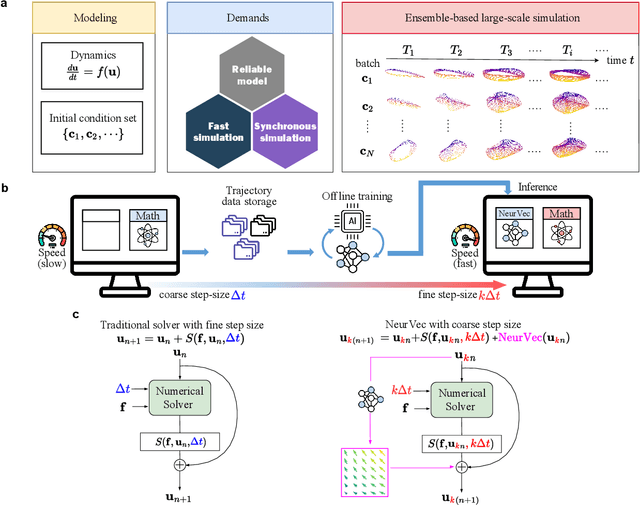
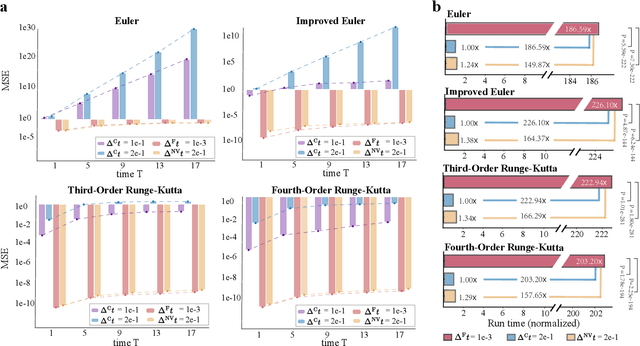
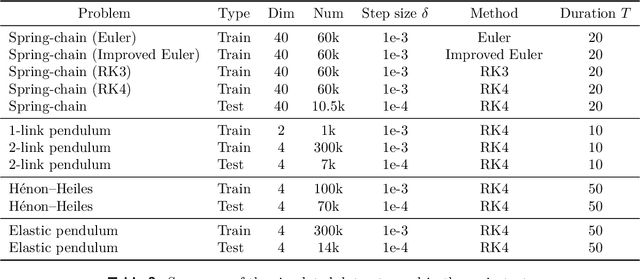
Ensemble-based large-scale simulation of dynamical systems is essential to a wide range of science and engineering problems. Conventional numerical solvers used in the simulation are significantly limited by the step size for time integration, which hampers efficiency and feasibility especially when high accuracy is desired. To overcome this limitation, we propose a data-driven corrector method that allows using large step sizes while compensating for the integration error for high accuracy. This corrector is represented in the form of a vector-valued function and is modeled by a neural network to regress the error in the phase space. Hence we name the corrector neural vector (NeurVec). We show that NeurVec can achieve the same accuracy as traditional solvers with much larger step sizes. We empirically demonstrate that NeurVec can accelerate a variety of numerical solvers significantly and overcome the stability restriction of these solvers. Our results on benchmark problems, ranging from high-dimensional problems to chaotic systems, suggest that NeurVec is capable of capturing the leading error term and maintaining the statistics of ensemble forecasts.

The Lottery Ticket Hypothesis for Self-attention in Convolutional Neural Network

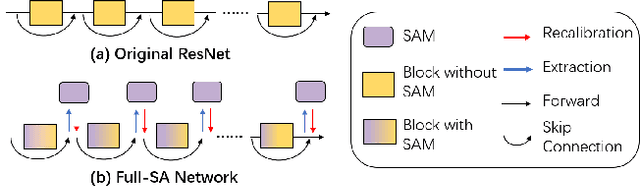
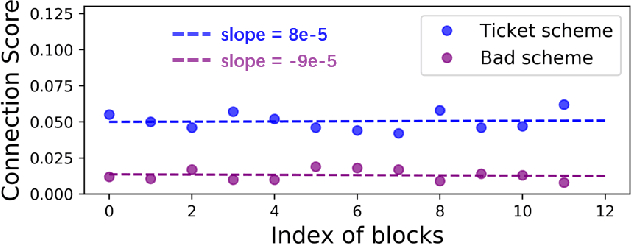
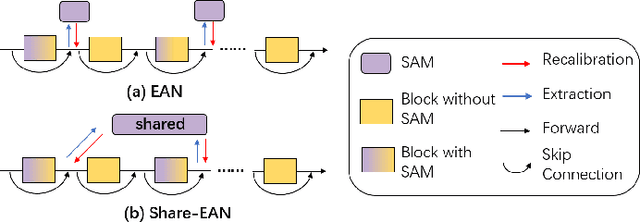
Recently many plug-and-play self-attention modules (SAMs) are proposed to enhance the model generalization by exploiting the internal information of deep convolutional neural networks (CNNs). In general, previous works ignore where to plug in the SAMs since they connect the SAMs individually with each block of the entire CNN backbone for granted, leading to incremental computational cost and the number of parameters with the growth of network depth. However, we empirically find and verify some counterintuitive phenomena that: (a) Connecting the SAMs to all the blocks may not always bring the largest performance boost, and connecting to partial blocks would be even better; (b) Adding the SAMs to a CNN may not always bring a performance boost, and instead it may even harm the performance of the original CNN backbone. Therefore, we articulate and demonstrate the Lottery Ticket Hypothesis for Self-attention Networks: a full self-attention network contains a subnetwork with sparse self-attention connections that can (1) accelerate inference, (2) reduce extra parameter increment, and (3) maintain accuracy. In addition to the empirical evidence, this hypothesis is also supported by our theoretical evidence. Furthermore, we propose a simple yet effective reinforcement-learning-based method to search the ticket, i.e., the connection scheme that satisfies the three above-mentioned conditions. Extensive experiments on widely-used benchmark datasets and popular self-attention networks show the effectiveness of our method. Besides, our experiments illustrate that our searched ticket has the capacity of transferring to some vision tasks, e.g., crowd counting and segmentation.