Hardeep Bassi
From noisy observables to accurate ground state energies: a quantum classical signal subspace approach with denoising
May 15, 2025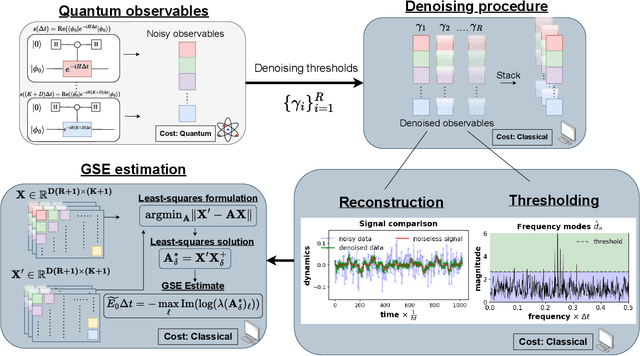
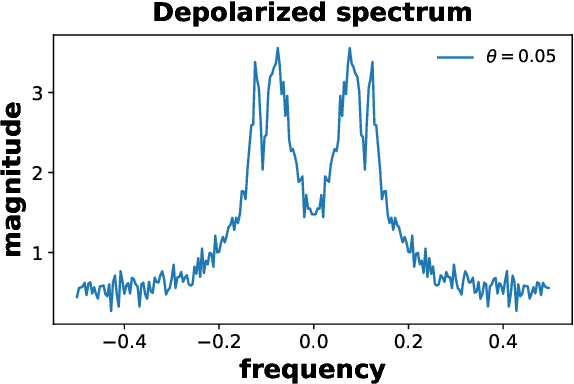
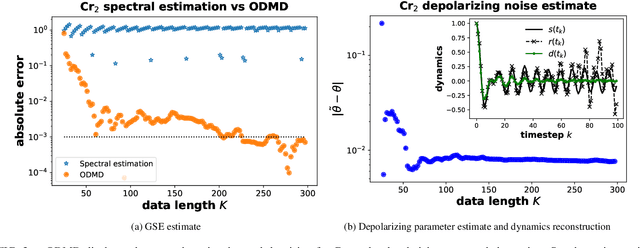
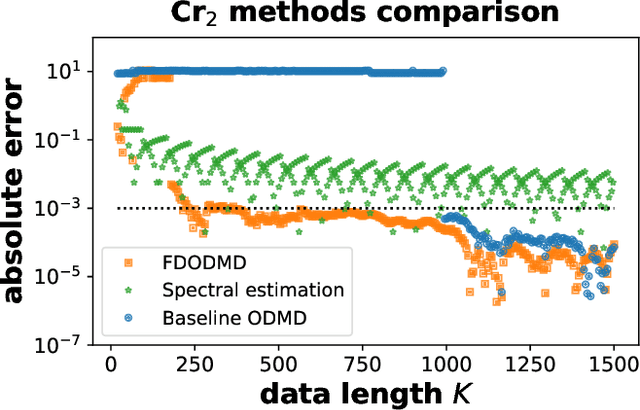
Abstract:We propose a hybrid quantum-classical algorithm for ground state energy (GSE) estimation that remains robust to highly noisy data and exhibits low sensitivity to hyperparameter tuning. Our approach -- Fourier Denoising Observable Dynamic Mode Decomposition (FDODMD) -- combines Fourier-based denoising thresholding to suppress spurious noise modes with observable dynamic mode decomposition (ODMD), a quantum-classical signal subspace method. By applying ODMD to an ensemble of denoised time-domain trajectories, FDODMD reliably estimates the system's eigenfrequencies. We also provide an error analysis of FDODMD. Numerical experiments on molecular systems demonstrate that FDODMD achieves convergence in high-noise regimes inaccessible to baseline methods under a limited quantum computational budget, while accelerating spectral estimation in intermediate-noise regimes. Importantly, this performance gain is entirely classical, requiring no additional quantum overhead and significantly reducing overall quantum resource demands.
Nonlinear Optimal Control of Electron Dynamics within Hartree-Fock Theory
Dec 04, 2024Abstract:Consider the problem of determining the optimal applied electric field to drive a molecule from an initial state to a desired target state. For even moderately sized molecules, solving this problem directly using the exact equations of motion -- the time-dependent Schr\"odinger equation (TDSE) -- is numerically intractable. We present a solution of this problem within time-dependent Hartree-Fock (TDHF) theory, a mean field approximation of the TDSE. Optimality is defined in terms of minimizing the total control effort while maximizing the overlap between desired and achieved target states. We frame this problem as an optimization problem constrained by the nonlinear TDHF equations; we solve it using trust region optimization with gradients computed via a custom-built adjoint state method. For three molecular systems, we show that with very small neural network parametrizations of the control, our method yields solutions that achieve desired targets within acceptable constraints and tolerances.
Learning nonlinear integral operators via Recurrent Neural Networks and its application in solving Integro-Differential Equations
Oct 13, 2023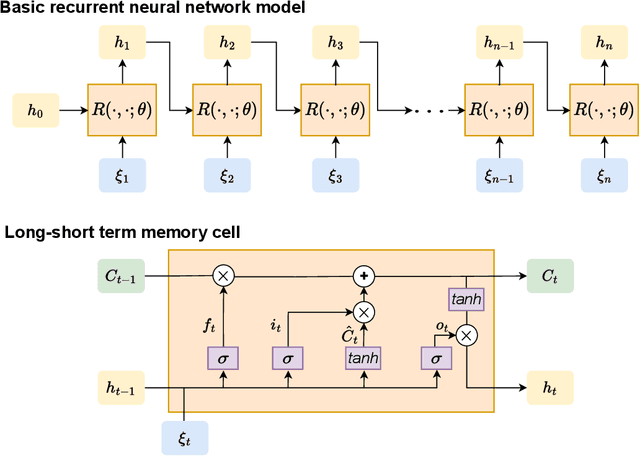

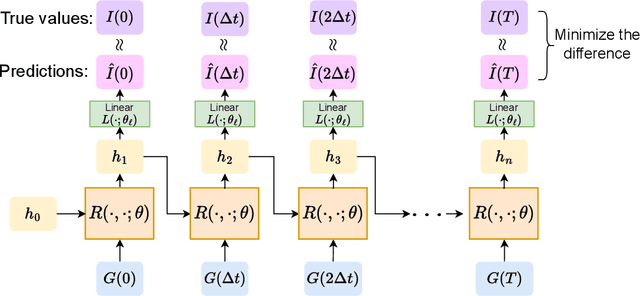
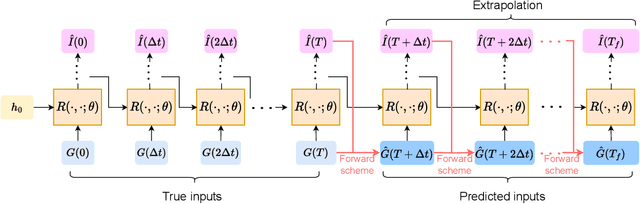
Abstract:In this paper, we propose using LSTM-RNNs (Long Short-Term Memory-Recurrent Neural Networks) to learn and represent nonlinear integral operators that appear in nonlinear integro-differential equations (IDEs). The LSTM-RNN representation of the nonlinear integral operator allows us to turn a system of nonlinear integro-differential equations into a system of ordinary differential equations for which many efficient solvers are available. Furthermore, because the use of LSTM-RNN representation of the nonlinear integral operator in an IDE eliminates the need to perform a numerical integration in each numerical time evolution step, the overall temporal cost of the LSTM-RNN-based IDE solver can be reduced to $O(n_T)$ from $O(n_T^2)$ if a $n_T$-step trajectory is to be computed. We illustrate the efficiency and robustness of this LSTM-RNN-based numerical IDE solver with a model problem. Additionally, we highlight the generalizability of the learned integral operator by applying it to IDEs driven by different external forces. As a practical application, we show how this methodology can effectively solve the Dyson's equation for quantum many-body systems.
Learning to predict synchronization of coupled oscillators on heterogeneous graphs
Dec 28, 2020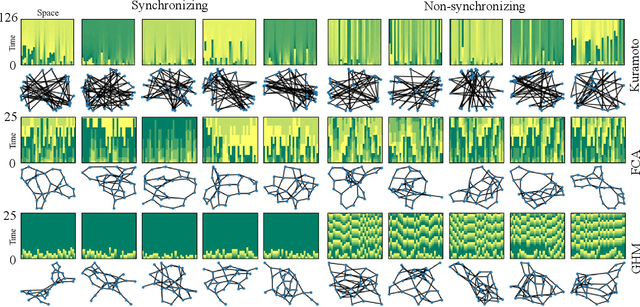
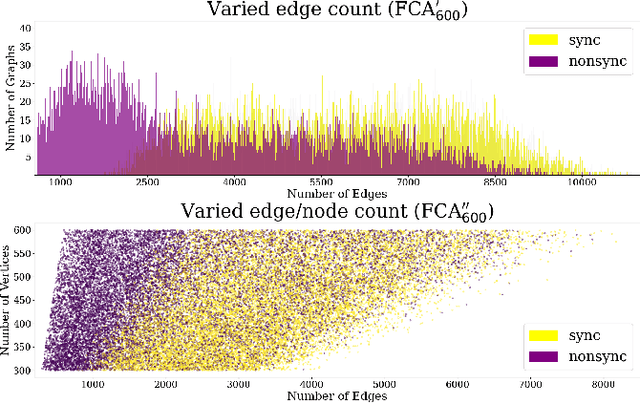
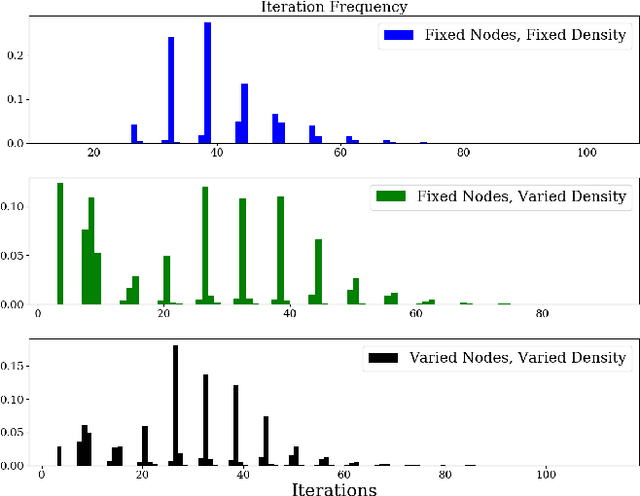
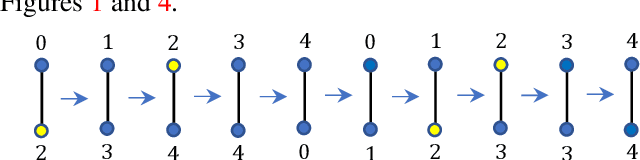
Abstract:Suppose we are given a system of coupled oscillators on an arbitrary graph along with the trajectory of the system during some period. Can we predict whether the system will eventually synchronize? This is an important but analytically intractable question especially when the structure of the underlying graph is highly varied. In this work, we take an entirely different approach that we call "learning to predict synchronization" (L2PSync), by viewing it as a classification problem for sets of graphs paired with initial dynamics into two classes: `synchronizing' or `non-synchronizing'. Our conclusion is that, once trained on large enough datasets of synchronizing and non-synchronizing dynamics on heterogeneous sets of graphs, a number of binary classification algorithms can successfully predict the future of an unknown system with surprising accuracy. We also propose an "ensemble prediction" algorithm that scales up our method to large graphs by training on dynamics observed from multiple random subgraphs. We find that in many instances, the first few iterations of the dynamics are far more important than the static features of the graphs. We demonstrate our method on three models of continuous and discrete coupled oscillators -- The Kuramoto model, the Firefly Cellular Automata, and the Greenberg-Hastings model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge