Learning to predict synchronization of coupled oscillators on heterogeneous graphs
Paper and Code
Dec 28, 2020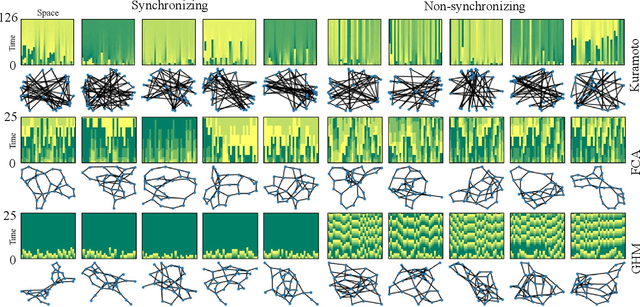
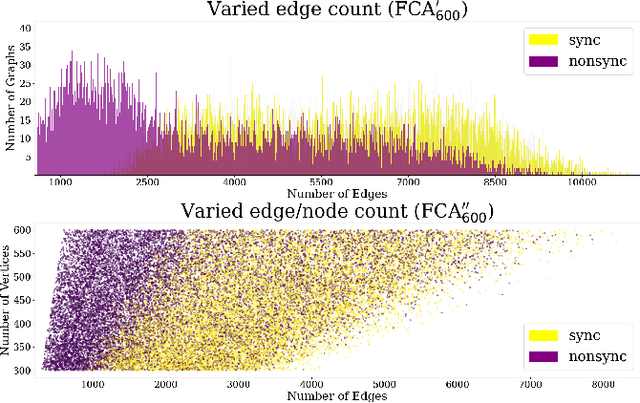
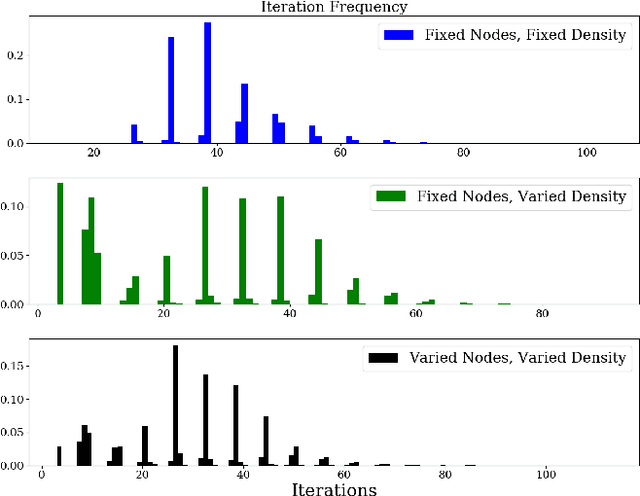
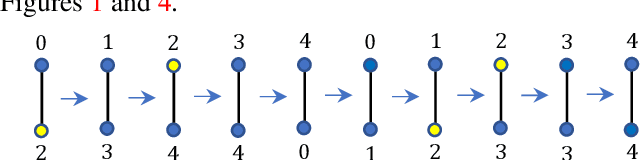
Suppose we are given a system of coupled oscillators on an arbitrary graph along with the trajectory of the system during some period. Can we predict whether the system will eventually synchronize? This is an important but analytically intractable question especially when the structure of the underlying graph is highly varied. In this work, we take an entirely different approach that we call "learning to predict synchronization" (L2PSync), by viewing it as a classification problem for sets of graphs paired with initial dynamics into two classes: `synchronizing' or `non-synchronizing'. Our conclusion is that, once trained on large enough datasets of synchronizing and non-synchronizing dynamics on heterogeneous sets of graphs, a number of binary classification algorithms can successfully predict the future of an unknown system with surprising accuracy. We also propose an "ensemble prediction" algorithm that scales up our method to large graphs by training on dynamics observed from multiple random subgraphs. We find that in many instances, the first few iterations of the dynamics are far more important than the static features of the graphs. We demonstrate our method on three models of continuous and discrete coupled oscillators -- The Kuramoto model, the Firefly Cellular Automata, and the Greenberg-Hastings model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge