Accelerating Numerical Solvers for Large-Scale Simulation of Dynamical System via NeurVec
Paper and Code
Aug 07, 2022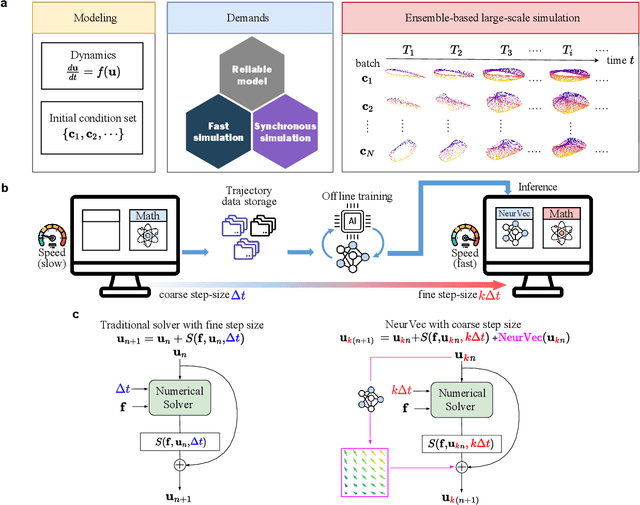

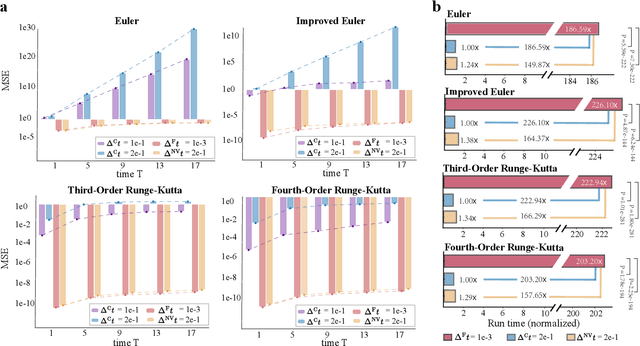
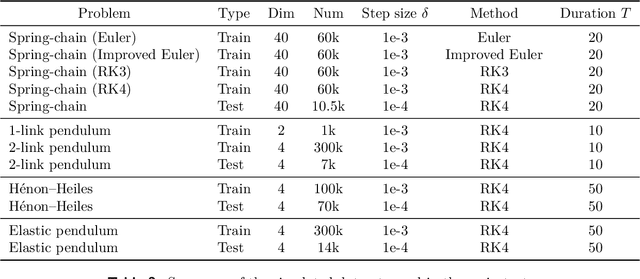
Ensemble-based large-scale simulation of dynamical systems is essential to a wide range of science and engineering problems. Conventional numerical solvers used in the simulation are significantly limited by the step size for time integration, which hampers efficiency and feasibility especially when high accuracy is desired. To overcome this limitation, we propose a data-driven corrector method that allows using large step sizes while compensating for the integration error for high accuracy. This corrector is represented in the form of a vector-valued function and is modeled by a neural network to regress the error in the phase space. Hence we name the corrector neural vector (NeurVec). We show that NeurVec can achieve the same accuracy as traditional solvers with much larger step sizes. We empirically demonstrate that NeurVec can accelerate a variety of numerical solvers significantly and overcome the stability restriction of these solvers. Our results on benchmark problems, ranging from high-dimensional problems to chaotic systems, suggest that NeurVec is capable of capturing the leading error term and maintaining the statistics of ensemble forecasts.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge