Probing reaction channels via reinforcement learning

We propose a reinforcement learning based method to identify important configurations that connect reactant and product states along chemical reaction paths. By shooting multiple trajectories from these configurations, we can generate an ensemble of configurations that concentrate on the transition path ensemble. This configuration ensemble can be effectively employed in a neural network-based partial differential equation solver to obtain an approximation solution of a restricted Backward Kolmogorov equation, even when the dimension of the problem is very high. The resulting solution, known as the committor function, encodes mechanistic information for the reaction and can in turn be used to evaluate reaction rates.

Reinforcement learning of rare diffusive dynamics

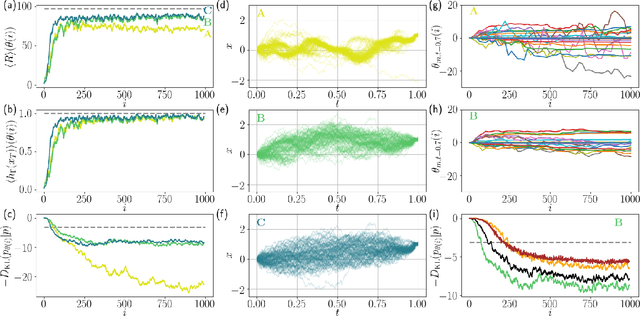
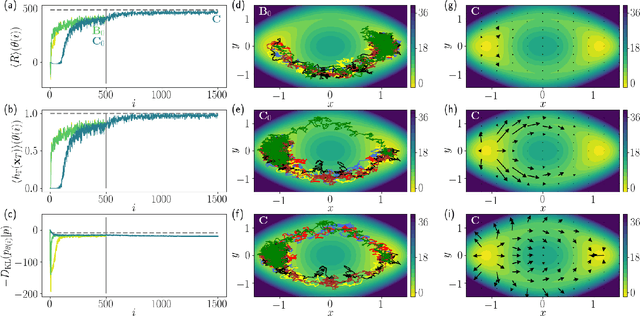
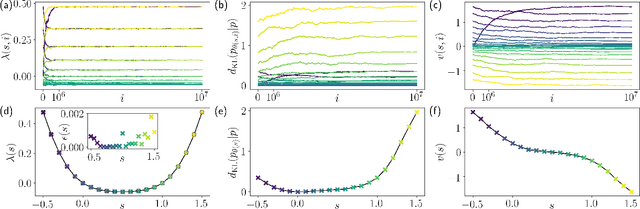
We present a method to probe rare molecular dynamics trajectories directly using reinforcement learning. We consider trajectories that are conditioned to transition between regions of configuration space in finite time, like those relevant in the study of reactive events, as well as trajectories exhibiting rare fluctuations of time-integrated quantities in the long time limit, like those relevant in the calculation of large deviation functions. In both cases, reinforcement learning techniques are used to optimize an added force that minimizes the Kullback-Leibler divergence between the conditioned trajectory ensemble and a driven one. Under the optimized added force, the system evolves the rare fluctuation as a typical one, affording a variational estimate of its likelihood in the original trajectory ensemble. Low variance gradients employing value functions are proposed to increase the convergence of the optimal force. The method we develop employing these gradients leads to efficient and accurate estimates of both the optimal force and the likelihood of the rare event for a variety of model systems.