Minibatch training of neural network ensembles via trajectory sampling

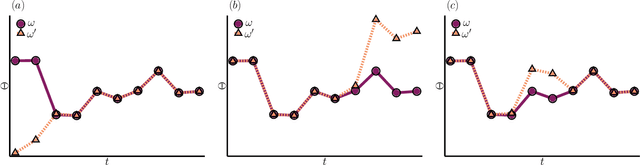
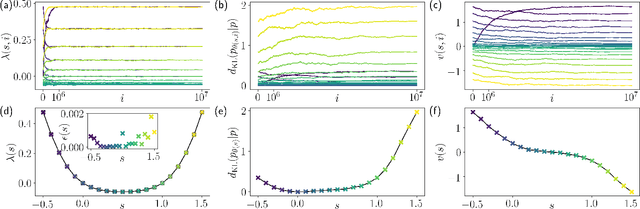
Most iterative neural network training methods use estimates of the loss function over small random subsets (or minibatches) of the data to update the parameters, which aid in decoupling the training time from the (often very large) size of the training datasets. Here, we show that a minibatch approach can also be used to train neural network ensembles (NNEs) via trajectory methods in a highly efficient manner. We illustrate this approach by training NNEs to classify images in the MNIST datasets. This method gives an improvement to the training times, allowing it to scale as the ratio of the size of the dataset to that of the average minibatch size which, in the case of MNIST, gives a computational improvement typically of two orders of magnitude. We highlight the advantage of using longer trajectories to represent NNEs, both for improved accuracy in inference and reduced update cost in terms of the samples needed in minibatch updates.

Reinforcement Learning with Tensor Networks: Application to Dynamical Large Deviations

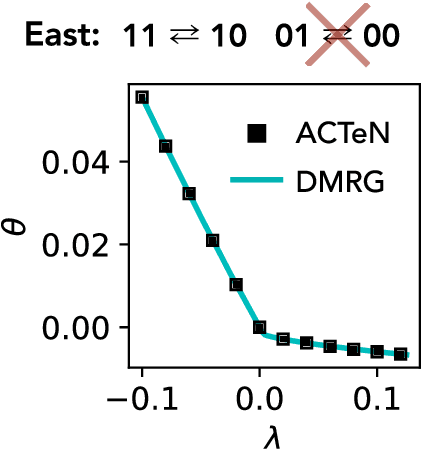
We present a framework to integrate tensor network (TN) methods with reinforcement learning (RL) for solving dynamical optimisation tasks. We consider the RL actor-critic method, a model-free approach for solving RL problems, and introduce TNs as the approximators for its policy and value functions. Our "actor-critic with tensor networks" (ACTeN) method is especially well suited to problems with large and factorisable state and action spaces. As an illustration of the applicability of ACTeN we solve the exponentially hard task of sampling rare trajectories in two paradigmatic stochastic models, the East model of glasses and the asymmetric simple exclusion process (ASEP), the latter being particularly challenging to other methods due to the absence of detailed balance. With substantial potential for further integration with the vast array of existing RL methods, the approach introduced here is promising both for applications in physics and to multi-agent RL problems more generally.

Training neural network ensembles via trajectory sampling

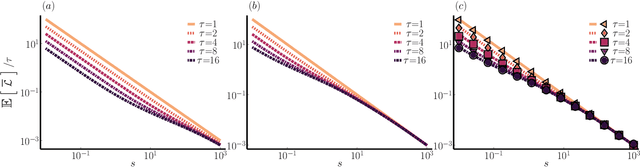
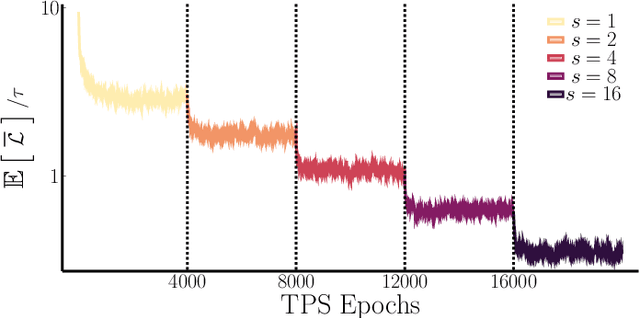
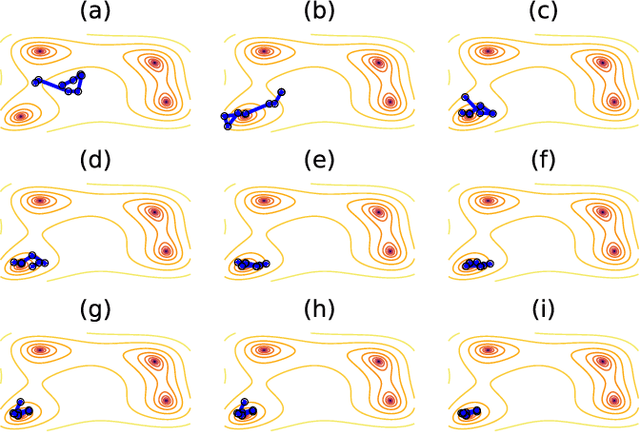
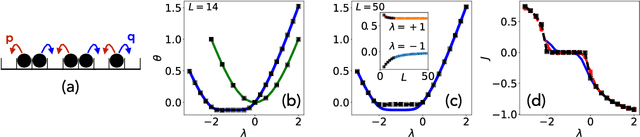
In machine learning, there is renewed interest in neural network ensembles (NNEs), whereby predictions are obtained as an aggregate from a diverse set of smaller models, rather than from a single larger model. Here, we show how to define and train a NNE using techniques from the study of rare trajectories in stochastic systems. We define an NNE in terms of the trajectory of the model parameters under a simple, and discrete in time, diffusive dynamics, and train the NNE by biasing these trajectories towards a small time-integrated loss, as controlled by appropriate counting fields which act as hyperparameters. We demonstrate the viability of this technique on a range of simple supervised learning tasks. We discuss potential advantages of our trajectory sampling approach compared with more conventional gradient based methods.

Reinforcement learning of rare diffusive dynamics

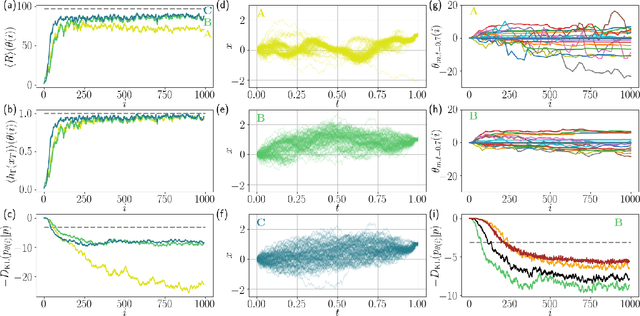
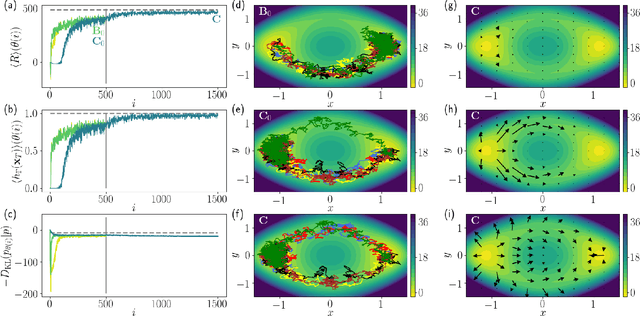
We present a method to probe rare molecular dynamics trajectories directly using reinforcement learning. We consider trajectories that are conditioned to transition between regions of configuration space in finite time, like those relevant in the study of reactive events, as well as trajectories exhibiting rare fluctuations of time-integrated quantities in the long time limit, like those relevant in the calculation of large deviation functions. In both cases, reinforcement learning techniques are used to optimize an added force that minimizes the Kullback-Leibler divergence between the conditioned trajectory ensemble and a driven one. Under the optimized added force, the system evolves the rare fluctuation as a typical one, affording a variational estimate of its likelihood in the original trajectory ensemble. Low variance gradients employing value functions are proposed to increase the convergence of the optimal force. The method we develop employing these gradients leads to efficient and accurate estimates of both the optimal force and the likelihood of the rare event for a variety of model systems.

A reinforcement learning approach to rare trajectory sampling

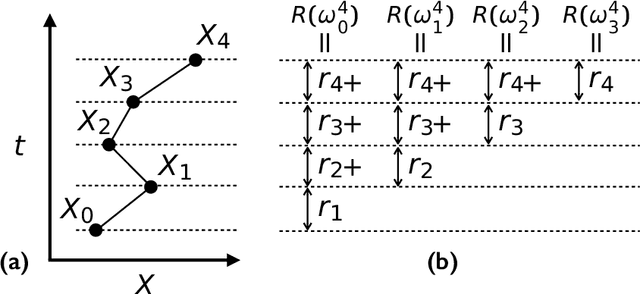
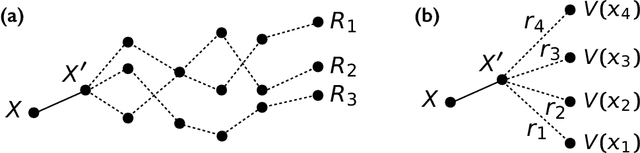
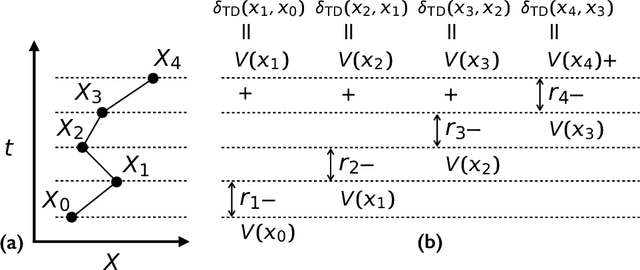
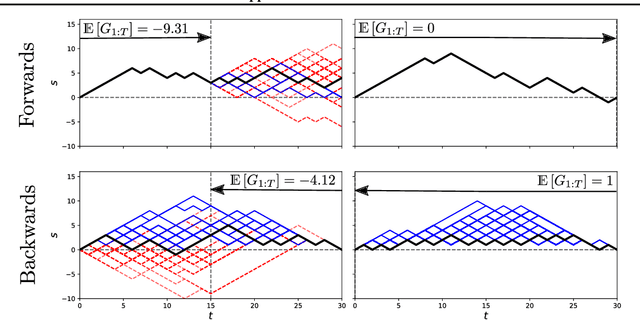
Very often when studying non-equilibrium systems one is interested in analysing dynamical behaviour that occurs with very low probability, so called rare events. In practice, since rare events are by definition atypical, they are often difficult to access in a statistically significant way. What are required are strategies to "make rare events typical" so that they can be generated on demand. Here we present such a general approach to adaptively construct a dynamics that efficiently samples atypical events. We do so by exploiting the methods of reinforcement learning (RL), which refers to the set of machine learning techniques aimed at finding the optimal behaviour to maximise a reward associated with the dynamics. We consider the general perspective of dynamical trajectory ensembles, whereby rare events are described in terms of ensemble reweighting. By minimising the distance between a reweighted ensemble and that of a suitably parametrised controlled dynamics we arrive at a set of methods similar to those of RL to numerically approximate the optimal dynamics that realises the rare behaviour of interest. As simple illustrations we consider in detail the problem of excursions of a random walker, for the case of rare events with a finite time horizon; and the problem of a studying current statistics of a particle hopping in a ring geometry, for the case of an infinite time horizon. We discuss natural extensions of the ideas presented here, including to continuous-time Markov systems, first passage time problems and non-Markovian dynamics.

A Tensor Network Approach to Finite Markov Decision Processes

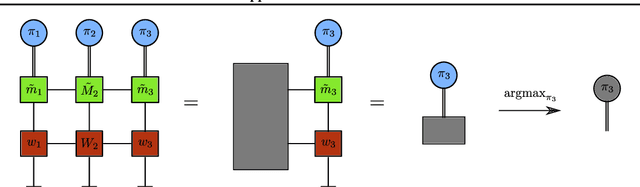
Tensor network (TN) techniques - often used in the context of quantum many-body physics - have shown promise as a tool for tackling machine learning (ML) problems. The application of TNs to ML, however, has mostly focused on supervised and unsupervised learning. Yet, with their direct connection to hidden Markov chains, TNs are also naturally suited to Markov decision processes (MDPs) which provide the foundation for reinforcement learning (RL). Here we introduce a general TN formulation of finite, episodic and discrete MDPs. We show how this formulation allows us to exploit algorithms developed for TNs for policy optimisation, the key aim of RL. As an application we consider the issue - formulated as an RL problem - of finding a stochastic evolution that satisfies specific dynamical conditions, using the simple example of random walk excursions as an illustration.