Minibatch training of neural network ensembles via trajectory sampling

Most iterative neural network training methods use estimates of the loss function over small random subsets (or minibatches) of the data to update the parameters, which aid in decoupling the training time from the (often very large) size of the training datasets. Here, we show that a minibatch approach can also be used to train neural network ensembles (NNEs) via trajectory methods in a highly efficient manner. We illustrate this approach by training NNEs to classify images in the MNIST datasets. This method gives an improvement to the training times, allowing it to scale as the ratio of the size of the dataset to that of the average minibatch size which, in the case of MNIST, gives a computational improvement typically of two orders of magnitude. We highlight the advantage of using longer trajectories to represent NNEs, both for improved accuracy in inference and reduced update cost in terms of the samples needed in minibatch updates.

Training neural network ensembles via trajectory sampling

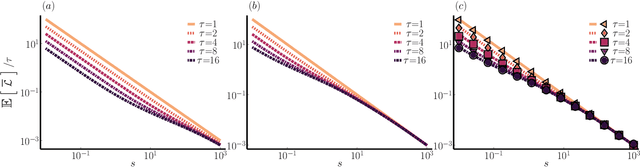
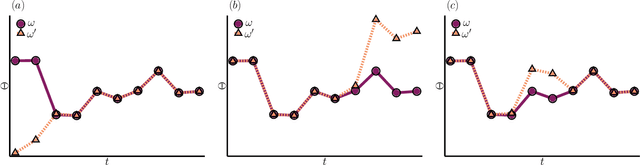
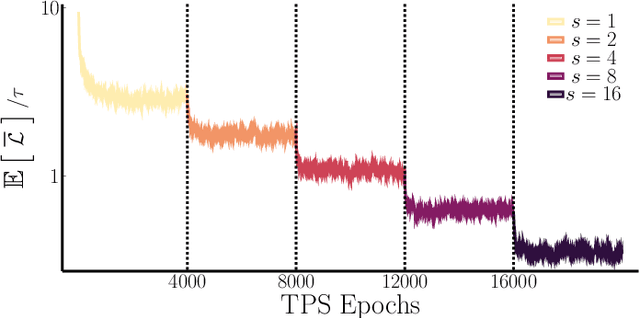
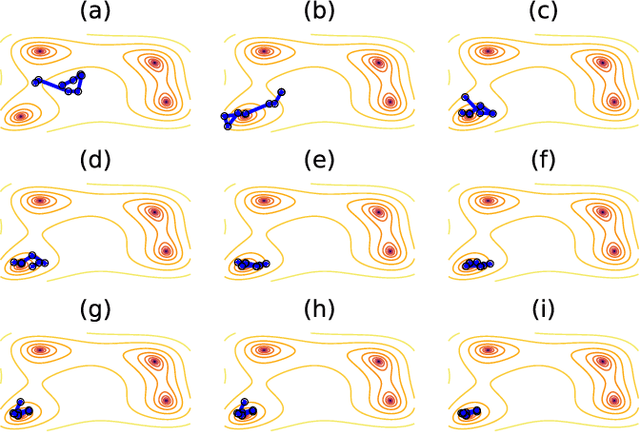
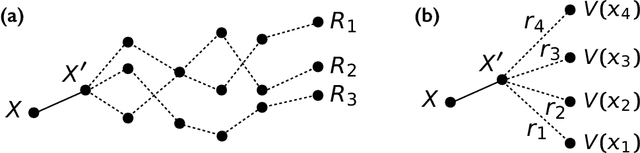
In machine learning, there is renewed interest in neural network ensembles (NNEs), whereby predictions are obtained as an aggregate from a diverse set of smaller models, rather than from a single larger model. Here, we show how to define and train a NNE using techniques from the study of rare trajectories in stochastic systems. We define an NNE in terms of the trajectory of the model parameters under a simple, and discrete in time, diffusive dynamics, and train the NNE by biasing these trajectories towards a small time-integrated loss, as controlled by appropriate counting fields which act as hyperparameters. We demonstrate the viability of this technique on a range of simple supervised learning tasks. We discuss potential advantages of our trajectory sampling approach compared with more conventional gradient based methods.

A reinforcement learning approach to rare trajectory sampling

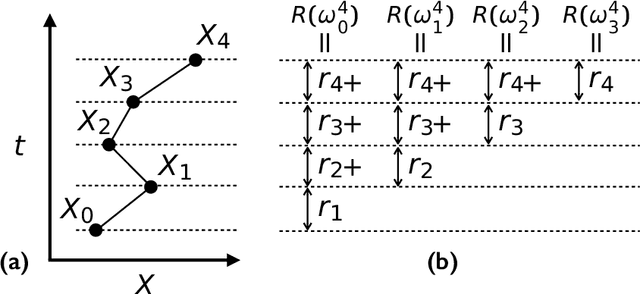
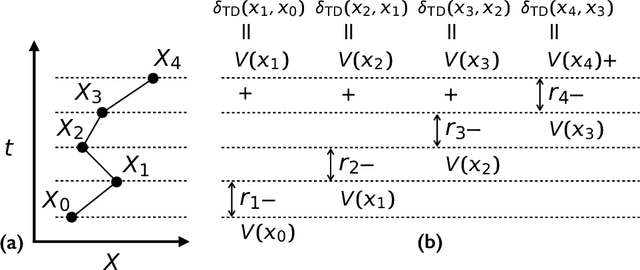
Very often when studying non-equilibrium systems one is interested in analysing dynamical behaviour that occurs with very low probability, so called rare events. In practice, since rare events are by definition atypical, they are often difficult to access in a statistically significant way. What are required are strategies to "make rare events typical" so that they can be generated on demand. Here we present such a general approach to adaptively construct a dynamics that efficiently samples atypical events. We do so by exploiting the methods of reinforcement learning (RL), which refers to the set of machine learning techniques aimed at finding the optimal behaviour to maximise a reward associated with the dynamics. We consider the general perspective of dynamical trajectory ensembles, whereby rare events are described in terms of ensemble reweighting. By minimising the distance between a reweighted ensemble and that of a suitably parametrised controlled dynamics we arrive at a set of methods similar to those of RL to numerically approximate the optimal dynamics that realises the rare behaviour of interest. As simple illustrations we consider in detail the problem of excursions of a random walker, for the case of rare events with a finite time horizon; and the problem of a studying current statistics of a particle hopping in a ring geometry, for the case of an infinite time horizon. We discuss natural extensions of the ideas presented here, including to continuous-time Markov systems, first passage time problems and non-Markovian dynamics.