On the generalization ability of coarse-grained molecular dynamics models for non-equilibrium processes

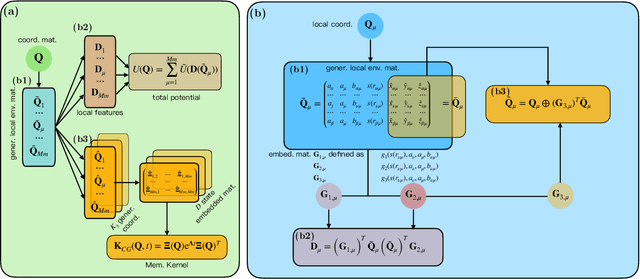
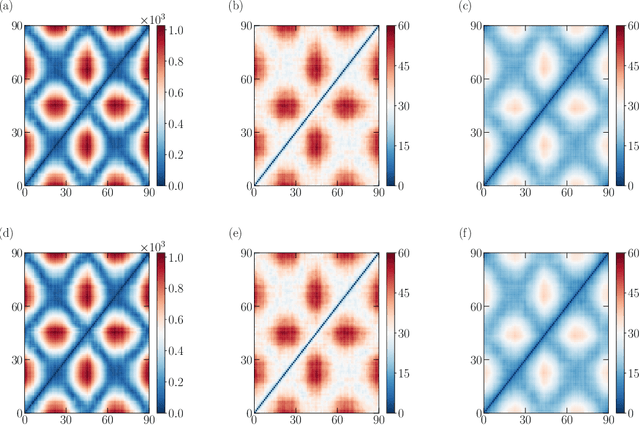
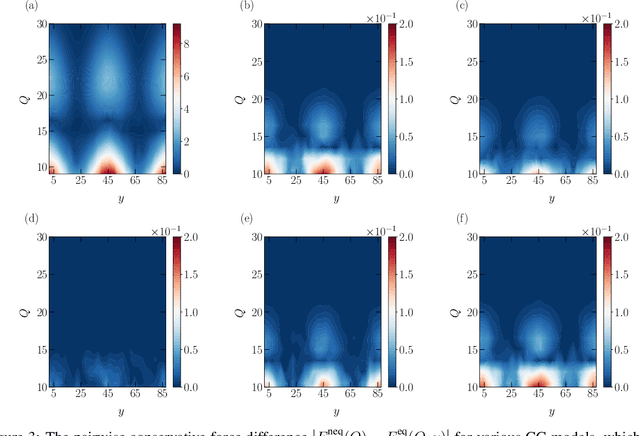
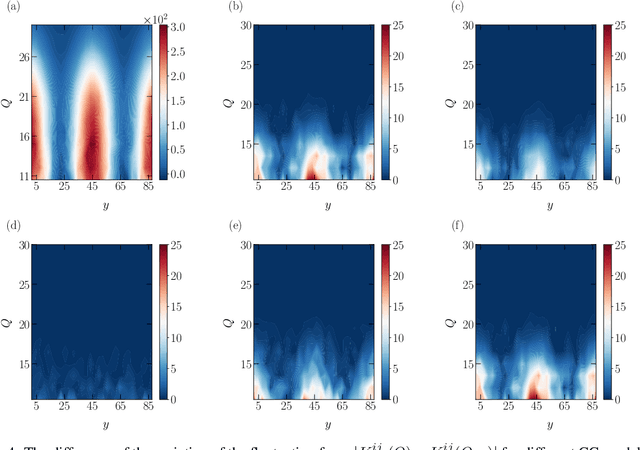
One essential goal of constructing coarse-grained molecular dynamics (CGMD) models is to accurately predict non-equilibrium processes beyond the atomistic scale. While a CG model can be constructed by projecting the full dynamics onto a set of resolved variables, the dynamics of the CG variables can recover the full dynamics only when the conditional distribution of the unresolved variables is close to the one associated with the particular projection operator. In particular, the model's applicability to various non-equilibrium processes is generally unwarranted due to the inconsistency in the conditional distribution. Here, we present a data-driven approach for constructing CGMD models that retain certain generalization ability for non-equilibrium processes. Unlike the conventional CG models based on pre-selected CG variables (e.g., the center of mass), the present CG model seeks a set of auxiliary CG variables based on the time-lagged independent component analysis to minimize the entropy contribution of the unresolved variables. This ensures the distribution of the unresolved variables under a broad range of non-equilibrium conditions approaches the one under equilibrium. Numerical results of a polymer melt system demonstrate the significance of this broadly-overlooked metric for the model's generalization ability, and the effectiveness of the present CG model for predicting the complex viscoelastic responses under various non-equilibrium flows.

Consensus-based construction of high-dimensional free energy surface

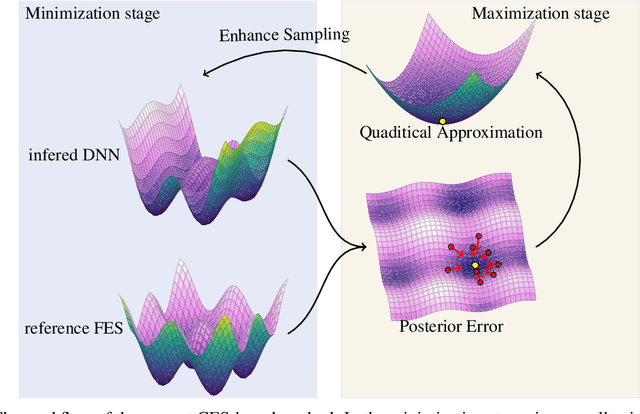
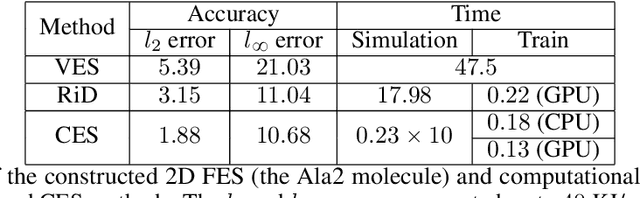
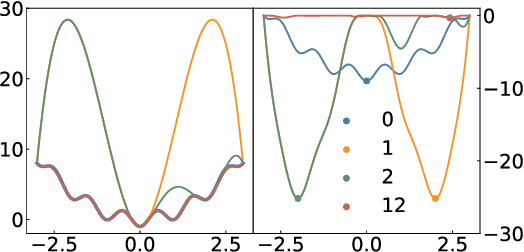
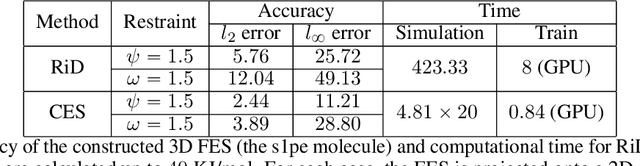
One essential problem in quantifying the collective behaviors of molecular systems lies in the accurate construction of free energy surfaces (FESs). The main challenges arise from the prevalence of energy barriers and the high dimensionality. Existing approaches are often based on sophisticated enhanced sampling methods to establish efficient exploration of the full-phase space. On the other hand, the collection of optimal sample points for the numerical approximation of FESs remains largely under-explored, where the discretization error could become dominant for systems with a large number of collective variables (CVs). We propose a consensus sampling-based approach by reformulating the construction as a minimax problem which simultaneously optimizes the function representation and the training set. In particular, the maximization step establishes a stochastic interacting particle system to achieve the adaptive sampling of the max-residue regime by modulating the exploitation of the Laplace approximation of the current loss function and the exploration of the uncharted phase space; the minimization step updates the FES approximation with the new training set. By iteratively solving the minimax problem, the present method essentially achieves an adversarial learning of the FESs with unified tasks for both phase space exploration and posterior error-enhanced sampling. We demonstrate the method by constructing the FESs of molecular systems with a number of CVs up to 30.

Reproducing Activation Function for Deep Learning

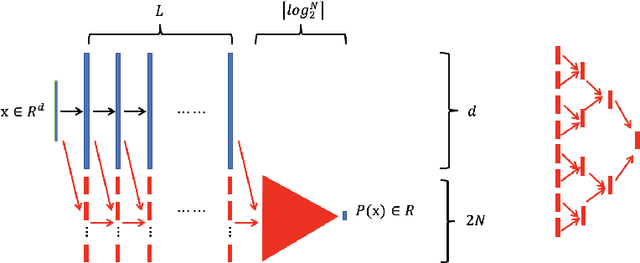
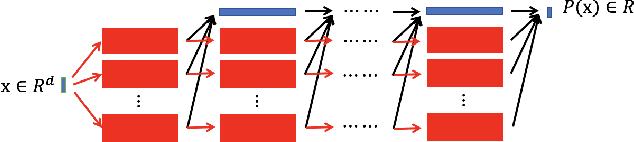
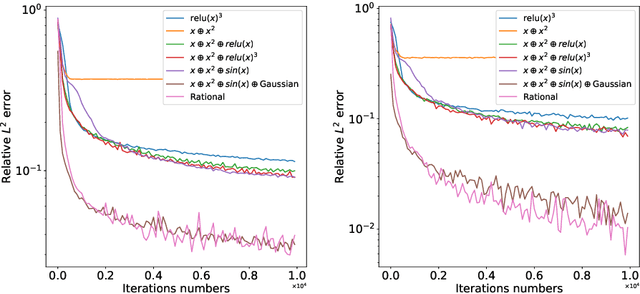
In this paper, we propose the reproducing activation function to improve deep learning accuracy for various applications ranging from computer vision problems to scientific computing problems. The idea of reproducing activation functions is to employ several basic functions and their learnable linear combination to construct neuron-wise data-driven activation functions for each neuron. Armed with such activation functions, deep neural networks can reproduce traditional approximation tools and, therefore, approximate target functions with a smaller number of parameters than traditional neural networks. In terms of training dynamics of deep learning, reproducing activation functions can generate neural tangent kernels with a better condition number than traditional activation functions lessening the spectral bias of deep learning. As demonstrated by extensive numerical tests, the proposed activation function can facilitate the convergence of deep learning optimization for a solution with higher accuracy than existing deep learning solvers for audio/image/video reconstruction, PDEs, and eigenvalue problems.

Quasi-Monte Carlo sampling for machine-learning partial differential equations

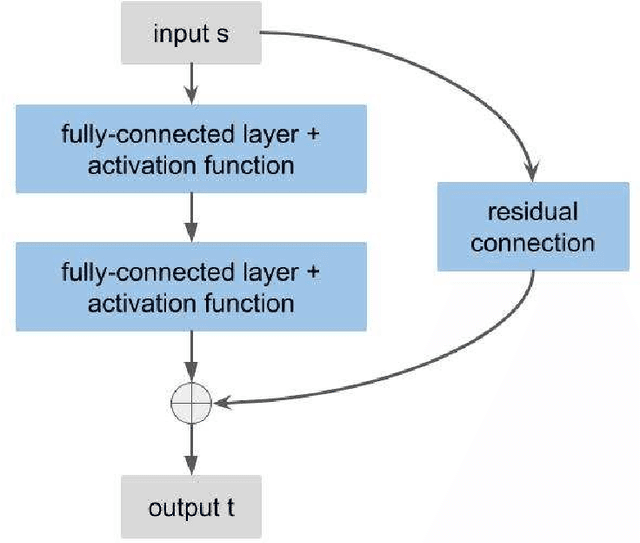
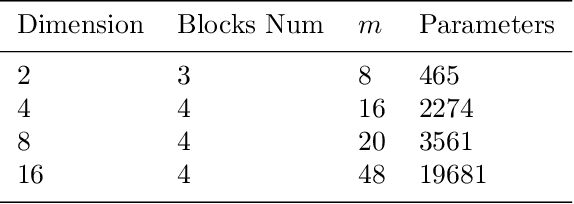
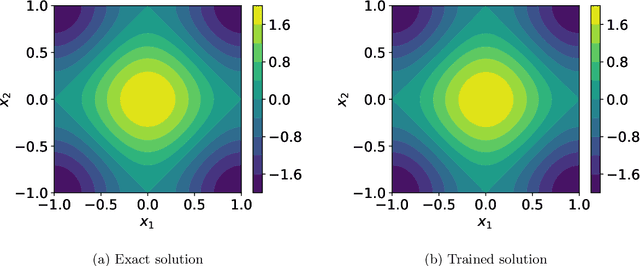
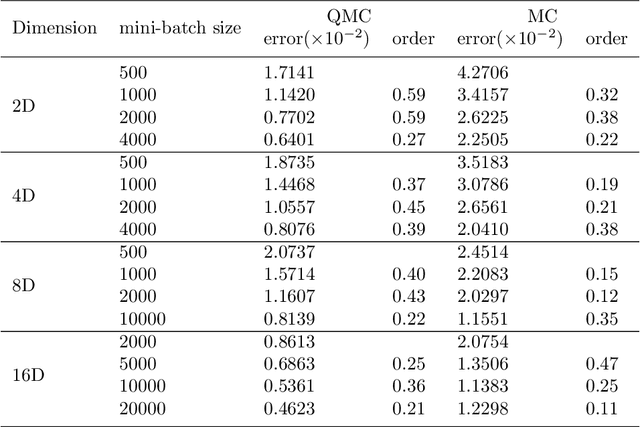
Solving partial differential equations in high dimensions by deep neural network has brought significant attentions in recent years. In many scenarios, the loss function is defined as an integral over a high-dimensional domain. Monte-Carlo method, together with the deep neural network, is used to overcome the curse of dimensionality, while classical methods fail. Often, a deep neural network outperforms classical numerical methods in terms of both accuracy and efficiency. In this paper, we propose to use quasi-Monte Carlo sampling, instead of Monte-Carlo method to approximate the loss function. To demonstrate the idea, we conduct numerical experiments in the framework of deep Ritz method proposed by Weinan E and Bing Yu. For the same accuracy requirement, it is observed that quasi-Monte Carlo sampling reduces the size of training data set by more than two orders of magnitude compared to that of MC method. Under some assumptions, we prove that quasi-Monte Carlo sampling together with the deep neural network generates a convergent series with rate proportional to the approximation accuracy of quasi-Monte Carlo method for numerical integration. Numerically the fitted convergence rate is a bit smaller, but the proposed approach always outperforms Monte Carlo method. It is worth mentioning that the convergence analysis is generic whenever a loss function is approximated by the quasi-Monte Carlo method, although observations here are based on deep Ritz method.

Connecting exciton diffusion with surface roughness via deep learning

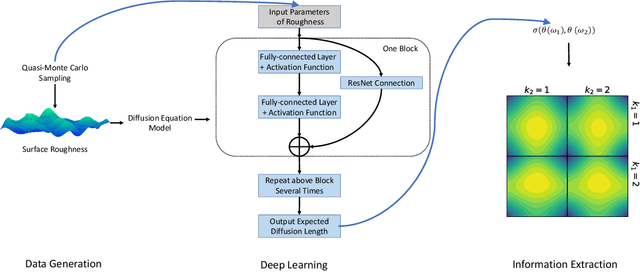
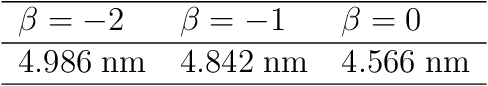
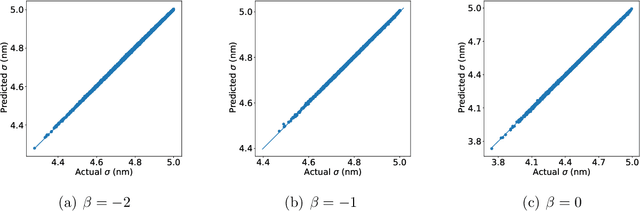
Exciton diffusion plays a vital role in the function of many organic semiconducting opto-electronic devices, where an accurate description requires precise control of heterojunctions. This poses a challenging problem because the parameterization of heterojunctions in high-dimensional random space is far beyond the capability of classical simulation tools. Here, we develop a novel method based on deep neural network to extract a function for exciton diffusion length on surface roughness with high accuracy and unprecedented efficiency, yielding an abundance of information over the entire parameter space. Our method provides a new strategy to analyze the impact of interfacial ordering on exciton diffusion and is expected to assist experimental design with tailored opto-electronic functionalities.