Xinyu AI Search: Enhanced Relevance and Comprehensive Results with Rich Answer Presentations

Traditional search engines struggle to synthesize fragmented information for complex queries, while generative AI search engines face challenges in relevance, comprehensiveness, and presentation. To address these limitations, we introduce Xinyu AI Search, a novel system that incorporates a query-decomposition graph to dynamically break down complex queries into sub-queries, enabling stepwise retrieval and generation. Our retrieval pipeline enhances diversity through multi-source aggregation and query expansion, while filtering and re-ranking strategies optimize passage relevance. Additionally, Xinyu AI Search introduces a novel approach for fine-grained, precise built-in citation and innovates in result presentation by integrating timeline visualization and textual-visual choreography. Evaluated on recent real-world queries, Xinyu AI Search outperforms eight existing technologies in human assessments, excelling in relevance, comprehensiveness, and insightfulness. Ablation studies validate the necessity of its key sub-modules. Our work presents the first comprehensive framework for generative AI search engines, bridging retrieval, generation, and user-centric presentation.

Physics-informed Temporal Alignment for Auto-regressive PDE Foundation Models

Auto-regressive partial differential equation (PDE) foundation models have shown great potential in handling time-dependent data. However, these models suffer from the shortcut problem deeply rooted in auto-regressive prediction, causing error accumulation. The challenge becomes particularly evident for out-of-distribution data, as the pretraining performance may approach random model initialization for downstream tasks with long-term dynamics. To deal with this problem, we propose physics-informed temporal alignment (PITA), a self-supervised learning framework inspired by inverse problem solving. Specifically, PITA aligns the physical dynamics discovered at different time steps on each given PDE trajectory by integrating physics-informed constraints into the self-supervision signal. The alignment is derived from observation data without relying on known physics priors, indicating strong generalization ability to the out-of-distribution data. Extensive experiments show that PITA significantly enhances the accuracy and robustness of existing foundation models on diverse time-dependent PDE data. The code is available at https://github.com/SCAILab-USTC/PITA.

STSA: Spatial-Temporal Semantic Alignment for Visual Dubbing

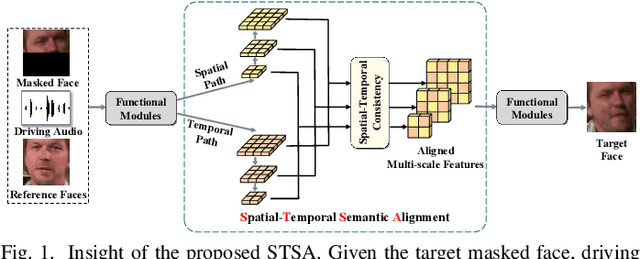
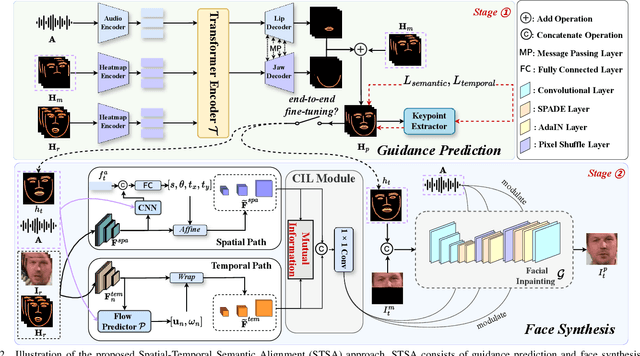
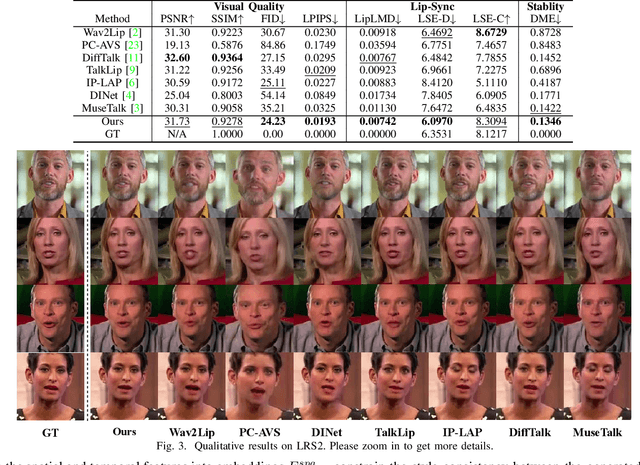
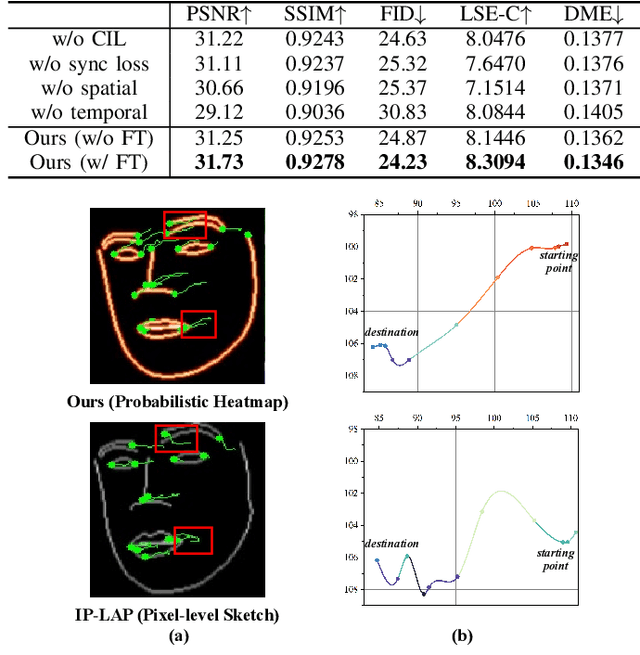
Existing audio-driven visual dubbing methods have achieved great success. Despite this, we observe that the semantic ambiguity between spatial and temporal domains significantly degrades the synthesis stability for the dynamic faces. We argue that aligning the semantic features from spatial and temporal domains is a promising approach to stabilizing facial motion. To achieve this, we propose a Spatial-Temporal Semantic Alignment (STSA) method, which introduces a dual-path alignment mechanism and a differentiable semantic representation. The former leverages a Consistent Information Learning (CIL) module to maximize the mutual information at multiple scales, thereby reducing the manifold differences between spatial and temporal domains. The latter utilizes probabilistic heatmap as ambiguity-tolerant guidance to avoid the abnormal dynamics of the synthesized faces caused by slight semantic jittering. Extensive experimental results demonstrate the superiority of the proposed STSA, especially in terms of image quality and synthesis stability. Pre-trained weights and inference code are available at https://github.com/SCAILab-USTC/STSA.

Solving multiscale elliptic problems by sparse radial basis function neural networks

Machine learning has been successfully applied to various fields of scientific computing in recent years. In this work, we propose a sparse radial basis function neural network method to solve elliptic partial differential equations (PDEs) with multiscale coefficients. Inspired by the deep mixed residual method, we rewrite the second-order problem into a first-order system and employ multiple radial basis function neural networks (RBFNNs) to approximate unknown functions in the system. To aviod the overfitting due to the simplicity of RBFNN, an additional regularization is introduced in the loss function. Thus the loss function contains two parts: the $L_2$ loss for the residual of the first-order system and boundary conditions, and the $\ell_1$ regularization term for the weights of radial basis functions (RBFs). An algorithm for optimizing the specific loss function is introduced to accelerate the training process. The accuracy and effectiveness of the proposed method are demonstrated through a collection of multiscale problems with scale separation, discontinuity and multiple scales from one to three dimensions. Notably, the $\ell_1$ regularization can achieve the goal of representing the solution by fewer RBFs. As a consequence, the total number of RBFs scales like $\mathcal{O}(\varepsilon^{-n\tau})$, where $\varepsilon$ is the smallest scale, $n$ is the dimensionality, and $\tau$ is typically smaller than $1$. It is worth mentioning that the proposed method not only has the numerical convergence and thus provides a reliable numerical solution in three dimensions when a classical method is typically not affordable, but also outperforms most other available machine learning methods in terms of accuracy and robustness.

Exploring the Optimal Choice for Generative Processes in Diffusion Models: Ordinary vs Stochastic Differential Equations

The diffusion model has shown remarkable success in computer vision, but it remains unclear whether ODE-based probability flow or SDE-based diffusion models are superior and under what circumstances. Comparing the two is challenging due to dependencies on data distribution, score training, and other numerical factors. In this paper, we examine the problem mathematically by examining two limiting scenarios: the ODE case and the large diffusion case. We first introduce a pulse-shape error to perturb the score function and analyze error accumulation, with a generalization to arbitrary error. Our findings indicate that when the perturbation occurs at the end of the generative process, the ODE model outperforms the SDE model (with a large diffusion coefficient). However, when the perturbation occurs earlier, the SDE model outperforms the ODE model, and we demonstrate that the error of sample generation due to pulse-shape error can be exponentially suppressed as the diffusion term's magnitude increases to infinity. Numerical validation of this phenomenon is provided using toy models such as Gaussian, Gaussian mixture models, and Swiss roll. Finally, we experiment with MNIST and observe that varying the diffusion coefficient can improve sample quality even when the score function is not well trained.

Quasi-Monte Carlo sampling for machine-learning partial differential equations

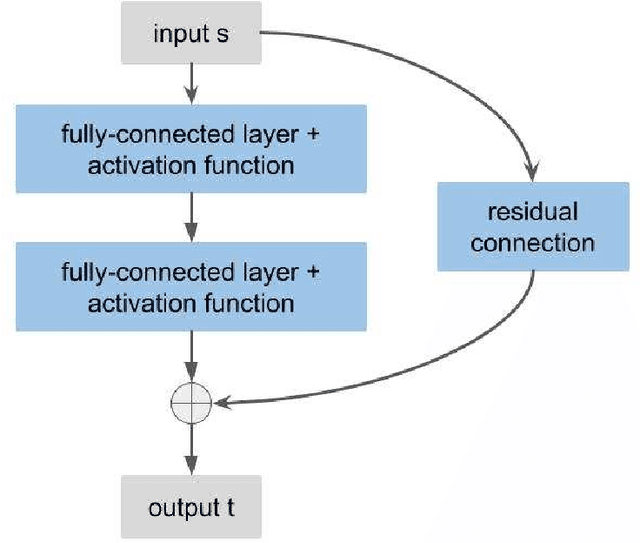
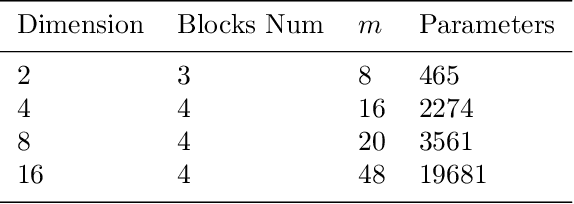
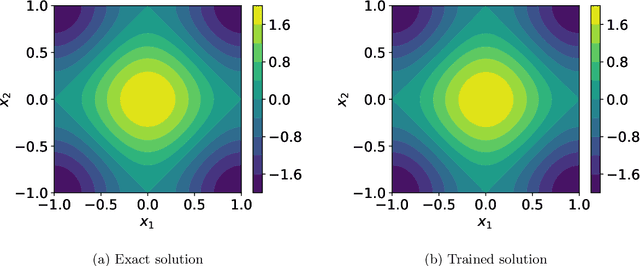
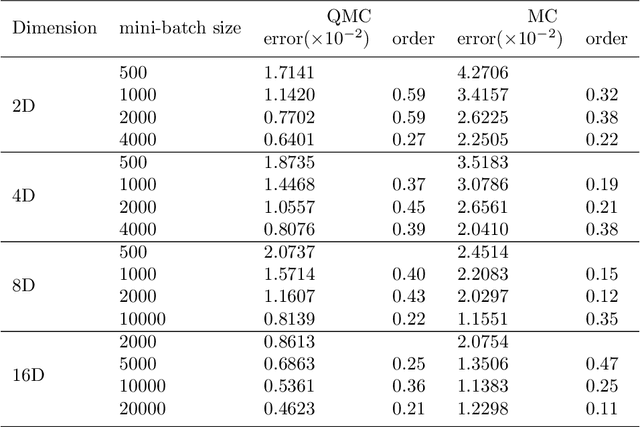
Solving partial differential equations in high dimensions by deep neural network has brought significant attentions in recent years. In many scenarios, the loss function is defined as an integral over a high-dimensional domain. Monte-Carlo method, together with the deep neural network, is used to overcome the curse of dimensionality, while classical methods fail. Often, a deep neural network outperforms classical numerical methods in terms of both accuracy and efficiency. In this paper, we propose to use quasi-Monte Carlo sampling, instead of Monte-Carlo method to approximate the loss function. To demonstrate the idea, we conduct numerical experiments in the framework of deep Ritz method proposed by Weinan E and Bing Yu. For the same accuracy requirement, it is observed that quasi-Monte Carlo sampling reduces the size of training data set by more than two orders of magnitude compared to that of MC method. Under some assumptions, we prove that quasi-Monte Carlo sampling together with the deep neural network generates a convergent series with rate proportional to the approximation accuracy of quasi-Monte Carlo method for numerical integration. Numerically the fitted convergence rate is a bit smaller, but the proposed approach always outperforms Monte Carlo method. It is worth mentioning that the convergence analysis is generic whenever a loss function is approximated by the quasi-Monte Carlo method, although observations here are based on deep Ritz method.

Connecting exciton diffusion with surface roughness via deep learning

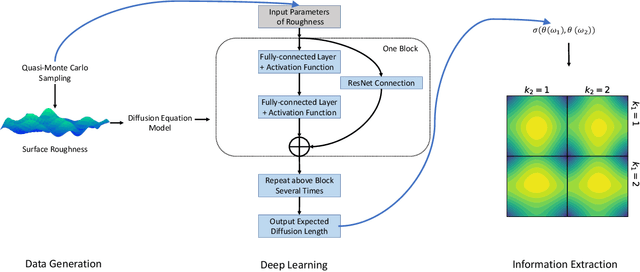
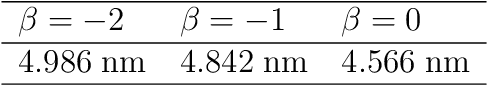
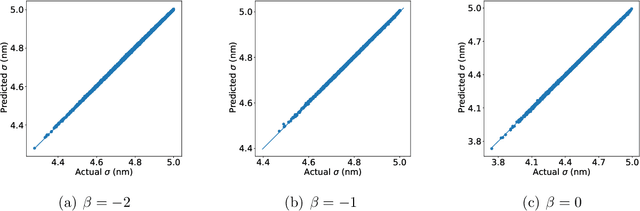
Exciton diffusion plays a vital role in the function of many organic semiconducting opto-electronic devices, where an accurate description requires precise control of heterojunctions. This poses a challenging problem because the parameterization of heterojunctions in high-dimensional random space is far beyond the capability of classical simulation tools. Here, we develop a novel method based on deep neural network to extract a function for exciton diffusion length on surface roughness with high accuracy and unprecedented efficiency, yielding an abundance of information over the entire parameter space. Our method provides a new strategy to analyze the impact of interfacial ordering on exciton diffusion and is expected to assist experimental design with tailored opto-electronic functionalities.