Quasi-Monte Carlo sampling for machine-learning partial differential equations
Paper and Code
Nov 05, 2019
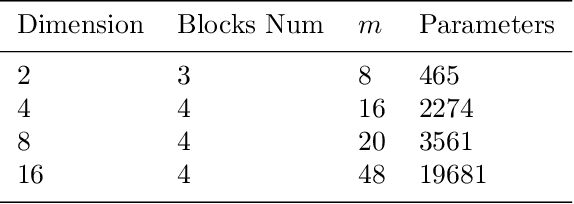
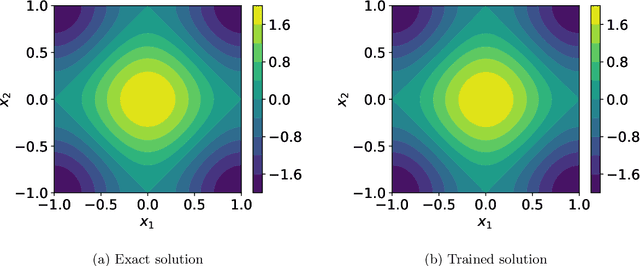
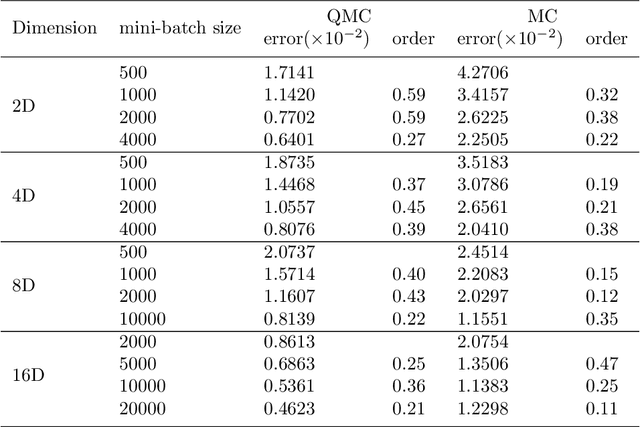
Solving partial differential equations in high dimensions by deep neural network has brought significant attentions in recent years. In many scenarios, the loss function is defined as an integral over a high-dimensional domain. Monte-Carlo method, together with the deep neural network, is used to overcome the curse of dimensionality, while classical methods fail. Often, a deep neural network outperforms classical numerical methods in terms of both accuracy and efficiency. In this paper, we propose to use quasi-Monte Carlo sampling, instead of Monte-Carlo method to approximate the loss function. To demonstrate the idea, we conduct numerical experiments in the framework of deep Ritz method proposed by Weinan E and Bing Yu. For the same accuracy requirement, it is observed that quasi-Monte Carlo sampling reduces the size of training data set by more than two orders of magnitude compared to that of MC method. Under some assumptions, we prove that quasi-Monte Carlo sampling together with the deep neural network generates a convergent series with rate proportional to the approximation accuracy of quasi-Monte Carlo method for numerical integration. Numerically the fitted convergence rate is a bit smaller, but the proposed approach always outperforms Monte Carlo method. It is worth mentioning that the convergence analysis is generic whenever a loss function is approximated by the quasi-Monte Carlo method, although observations here are based on deep Ritz method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge