On the generalization ability of coarse-grained molecular dynamics models for non-equilibrium processes
Paper and Code
Sep 17, 2024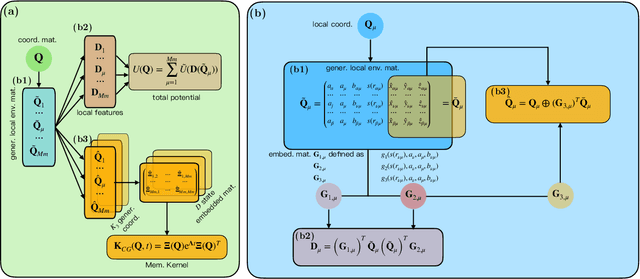
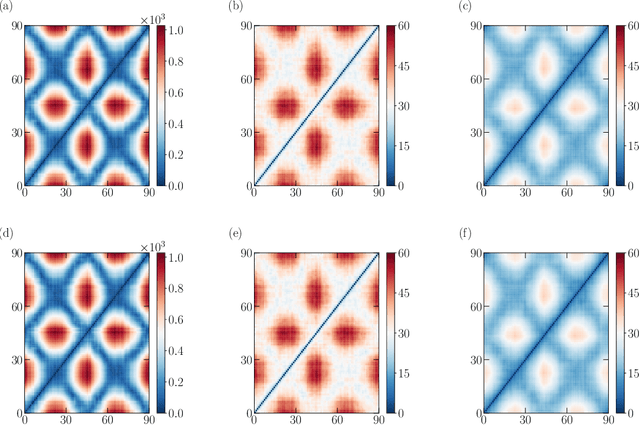
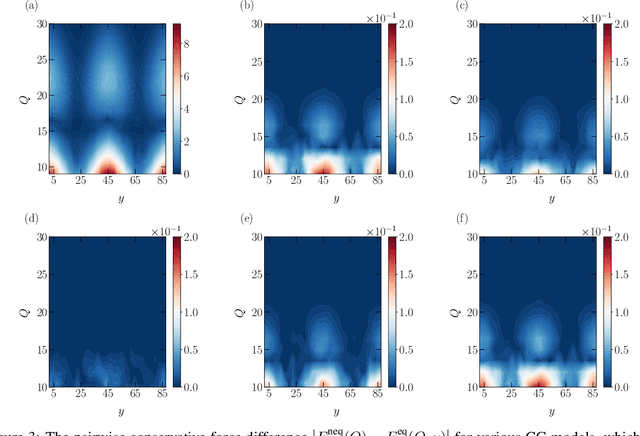
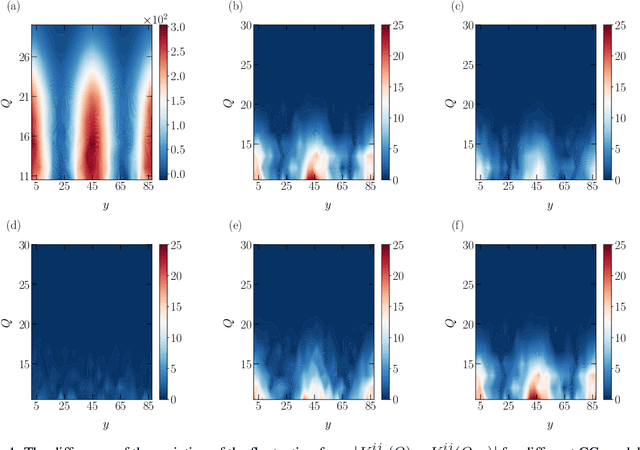
One essential goal of constructing coarse-grained molecular dynamics (CGMD) models is to accurately predict non-equilibrium processes beyond the atomistic scale. While a CG model can be constructed by projecting the full dynamics onto a set of resolved variables, the dynamics of the CG variables can recover the full dynamics only when the conditional distribution of the unresolved variables is close to the one associated with the particular projection operator. In particular, the model's applicability to various non-equilibrium processes is generally unwarranted due to the inconsistency in the conditional distribution. Here, we present a data-driven approach for constructing CGMD models that retain certain generalization ability for non-equilibrium processes. Unlike the conventional CG models based on pre-selected CG variables (e.g., the center of mass), the present CG model seeks a set of auxiliary CG variables based on the time-lagged independent component analysis to minimize the entropy contribution of the unresolved variables. This ensures the distribution of the unresolved variables under a broad range of non-equilibrium conditions approaches the one under equilibrium. Numerical results of a polymer melt system demonstrate the significance of this broadly-overlooked metric for the model's generalization ability, and the effectiveness of the present CG model for predicting the complex viscoelastic responses under various non-equilibrium flows.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge