A Statistical Assessment of Amortized Inference Under Signal-to-Noise Variation and Distribution Shift

Since the turn of the century, approximate Bayesian inference has steadily evolved as new computational techniques have been incorporated to handle increasingly complex and large-scale predictive problems. The recent success of deep neural networks and foundation models has now given rise to a new paradigm in statistical modeling, in which Bayesian inference can be amortized through large-scale learned predictors. In amortized inference, substantial computation is invested upfront to train a neural network that can subsequently produce approximate posterior or predictions at negligible marginal cost across a wide range of tasks. At deployment, amortized inference offers substantial computational savings compared with traditional Bayesian procedures, which generally require repeated likelihood evaluations or Monte Carlo simulations for predictions for each new dataset. Despite the growing popularity of amortized inference, its statistical interpretation and its role within Bayesian inference remain poorly understood. This paper presents statistical perspectives on the working principles of several major neural architectures, including feedforward networks, Deep Sets, and Transformers, and examines how these architectures naturally support amortized Bayesian inference. We discuss how these models perform structured approximation and probabilistic reasoning in ways that yield controlled generalization error across a wide range of deployment scenarios, and how these properties can be harnessed for Bayesian computation. Through simulation studies, we evaluate the accuracy, robustness, and uncertainty quantification of amortized inference under varying signal-to-noise ratios and distributional shifts, highlighting both its strengths and its limitations.

Empirical Bayes Estimation with Side Information: A Nonparametric Integrative Tweedie Approach

We investigate the problem of compound estimation of normal means while accounting for the presence of side information. Leveraging the empirical Bayes framework, we develop a nonparametric integrative Tweedie (NIT) approach that incorporates structural knowledge encoded in multivariate auxiliary data to enhance the precision of compound estimation. Our approach employs convex optimization tools to estimate the gradient of the log-density directly, enabling the incorporation of structural constraints. We conduct theoretical analyses of the asymptotic risk of NIT and establish the rate at which NIT converges to the oracle estimator. As the dimension of the auxiliary data increases, we accurately quantify the improvements in estimation risk and the associated deterioration in convergence rate. The numerical performance of NIT is illustrated through the analysis of both simulated and real data, demonstrating its superiority over existing methods.

Bootstrapped Edge Count Tests for Nonparametric Two-Sample Inference Under Heterogeneity

Nonparametric two-sample testing is a classical problem in inferential statistics. While modern two-sample tests, such as the edge count test and its variants, can handle multivariate and non-Euclidean data, contemporary gargantuan datasets often exhibit heterogeneity due to the presence of latent subpopulations. Direct application of these tests, without regulating for such heterogeneity, may lead to incorrect statistical decisions. We develop a new nonparametric testing procedure that accurately detects differences between the two samples in the presence of unknown heterogeneity in the data generation process. Our framework handles this latent heterogeneity through a composite null that entertains the possibility that the two samples arise from a mixture distribution with identical component distributions but with possibly different mixing weights. In this regime, we study the asymptotic behavior of weighted edge count test statistic and show that it can be effectively re-calibrated to detect arbitrary deviations from the composite null. For practical implementation we propose a Bootstrapped Weighted Edge Count test which involves a bootstrap-based calibration procedure that can be easily implemented across a wide range of heterogeneous regimes. A comprehensive simulation study and an application to detecting aberrant user behaviors in online games demonstrates the excellent non-asymptotic performance of the proposed test.

Structured Dynamic Pricing: Optimal Regret in a Global Shrinkage Model

We consider dynamic pricing strategies in a streamed longitudinal data set-up where the objective is to maximize, over time, the cumulative profit across a large number of customer segments. We consider a dynamic probit model with the consumers' preferences as well as price sensitivity varying over time. Building on the well-known finding that consumers sharing similar characteristics act in similar ways, we consider a global shrinkage structure, which assumes that the consumers' preferences across the different segments can be well approximated by a spatial autoregressive (SAR) model. In such a streamed longitudinal set-up, we measure the performance of a dynamic pricing policy via regret, which is the expected revenue loss compared to a clairvoyant that knows the sequence of model parameters in advance. We propose a pricing policy based on penalized stochastic gradient descent (PSGD) and explicitly characterize its regret as functions of time, the temporal variability in the model parameters as well as the strength of the auto-correlation network structure spanning the varied customer segments. Our regret analysis results not only demonstrate asymptotic optimality of the proposed policy but also show that for policy planning it is essential to incorporate available structural information as policies based on unshrunken models are highly sub-optimal in the aforementioned set-up.

Large-Scale Shrinkage Estimation under Markovian Dependence

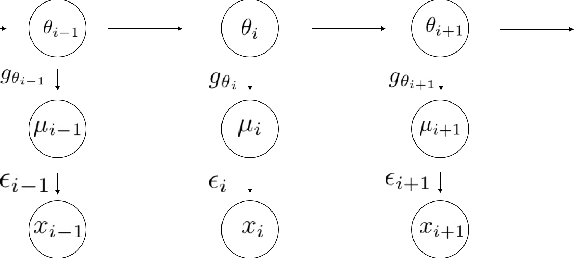
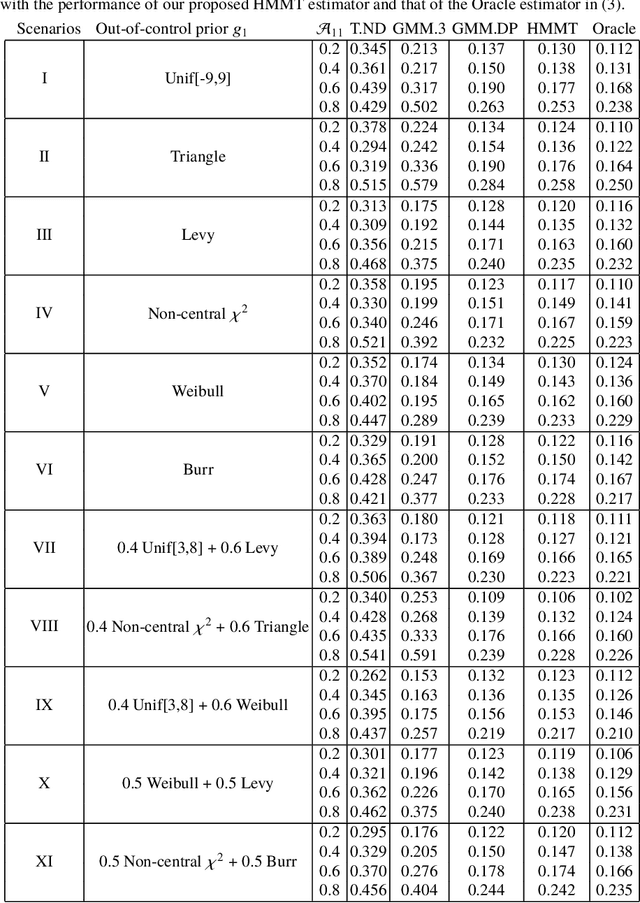
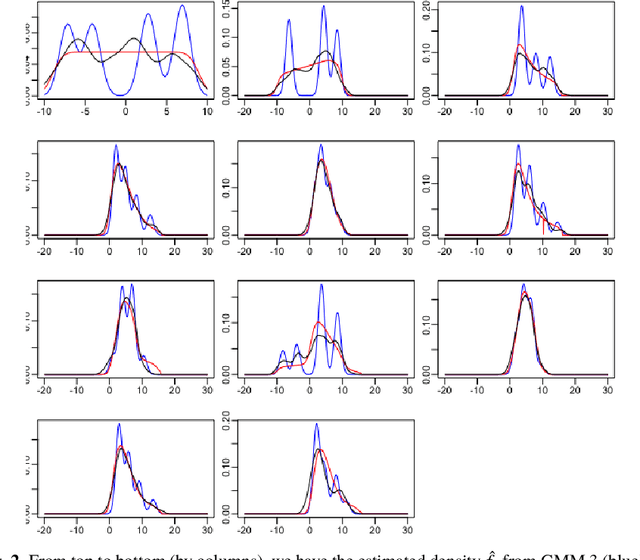
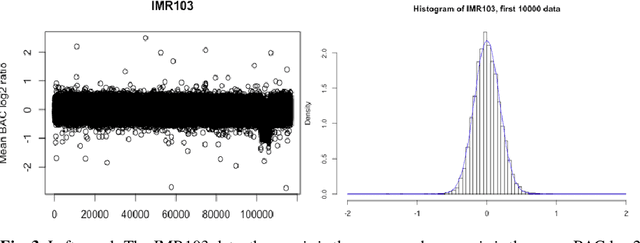
We consider the problem of simultaneous estimation of a sequence of dependent parameters that are generated from a hidden Markov model. Based on observing a noise contaminated vector of observations from such a sequence model, we consider simultaneous estimation of all the parameters irrespective of their hidden states under square error loss. We study the roles of statistical shrinkage for improved estimation of these dependent parameters. Being completely agnostic on the distributional properties of the unknown underlying Hidden Markov model, we develop a novel non-parametric shrinkage algorithm. Our proposed method elegantly combines \textit{Tweedie}-based non-parametric shrinkage ideas with efficient estimation of the hidden states under Markovian dependence. Based on extensive numerical experiments, we establish superior performance our our proposed algorithm compared to non-shrinkage based state-of-the-art parametric as well as non-parametric algorithms used in hidden Markov models. We provide decision theoretic properties of our methodology and exhibit its enhanced efficacy over popular shrinkage methods built under independence. We demonstrate the application of our methodology on real-world datasets for analyzing of temporally dependent social and economic indicators such as search trends and unemployment rates as well as estimating spatially dependent Copy Number Variations.