SAT: Data-light Uncertainty Set Merging via Synthetics, Aggregation, and Test Inversion

The integration of uncertainty sets has diverse applications but also presents challenges, particularly when only initial sets and their control levels are available, along with potential dependencies. Examples include merging confidence sets from different distributed sites with communication constraints, as well as combining conformal prediction sets generated by different learning algorithms or data splits. In this article, we introduce an efficient and flexible Synthetic, Aggregation, and Test inversion (SAT) approach to merge various potentially dependent uncertainty sets into a single set. The proposed method constructs a novel class of synthetic test statistics, aggregates them, and then derives merged sets through test inversion. Our approach leverages the duality between set estimation and hypothesis testing, ensuring reliable coverage in dependent scenarios. The procedure is data-light, meaning it relies solely on initial sets and control levels without requiring raw data, and it adapts to any user-specified initial uncertainty sets, accommodating potentially varying coverage levels. Theoretical analyses and numerical experiments confirm that SAT provides finite-sample coverage guarantees and achieves small set sizes.

Large-Scale Shrinkage Estimation under Markovian Dependence

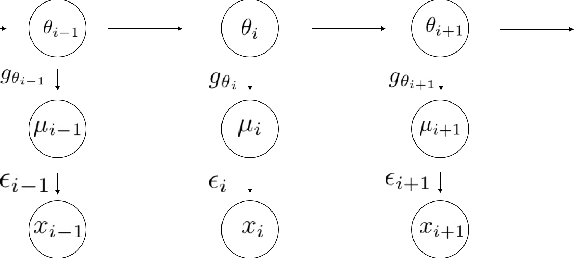
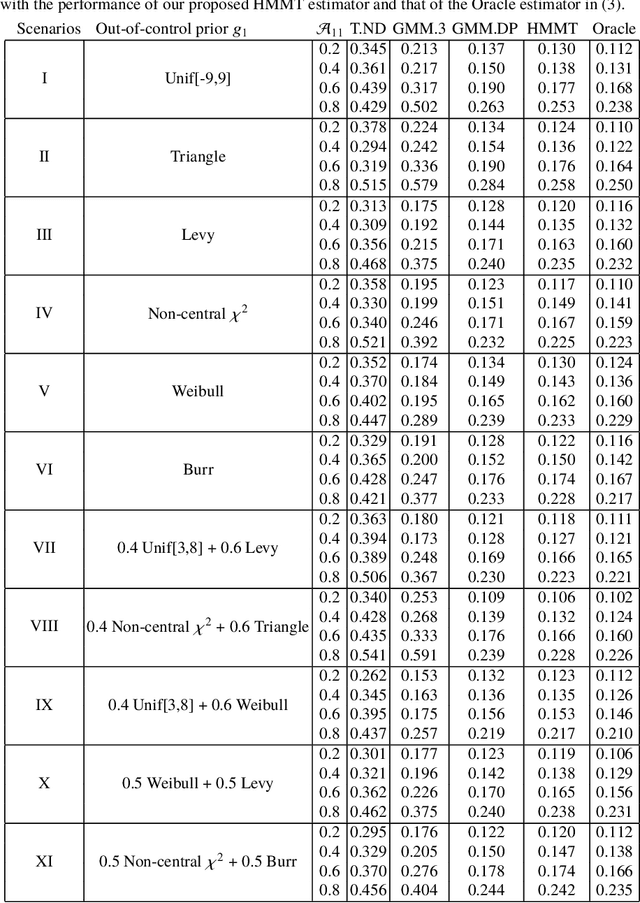
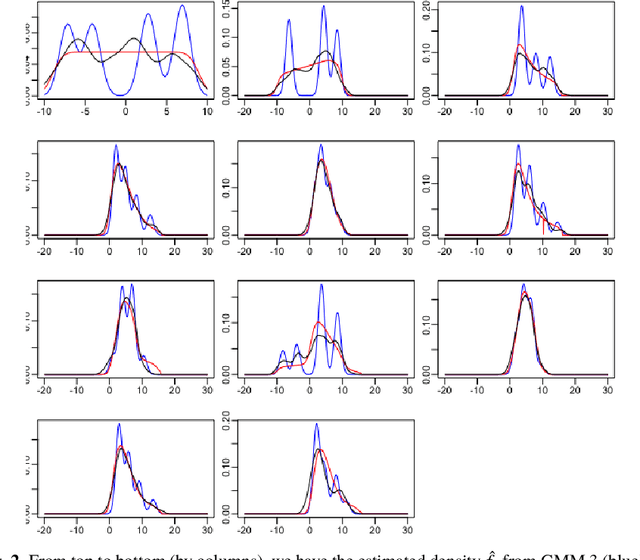
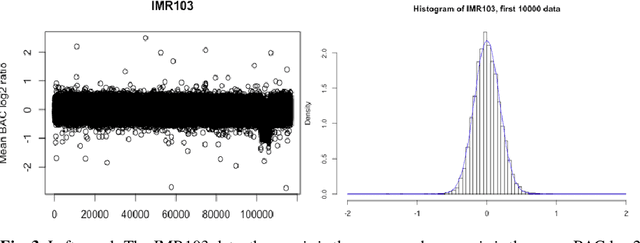
We consider the problem of simultaneous estimation of a sequence of dependent parameters that are generated from a hidden Markov model. Based on observing a noise contaminated vector of observations from such a sequence model, we consider simultaneous estimation of all the parameters irrespective of their hidden states under square error loss. We study the roles of statistical shrinkage for improved estimation of these dependent parameters. Being completely agnostic on the distributional properties of the unknown underlying Hidden Markov model, we develop a novel non-parametric shrinkage algorithm. Our proposed method elegantly combines \textit{Tweedie}-based non-parametric shrinkage ideas with efficient estimation of the hidden states under Markovian dependence. Based on extensive numerical experiments, we establish superior performance our our proposed algorithm compared to non-shrinkage based state-of-the-art parametric as well as non-parametric algorithms used in hidden Markov models. We provide decision theoretic properties of our methodology and exhibit its enhanced efficacy over popular shrinkage methods built under independence. We demonstrate the application of our methodology on real-world datasets for analyzing of temporally dependent social and economic indicators such as search trends and unemployment rates as well as estimating spatially dependent Copy Number Variations.

Structure-Adaptive Sequential Testing for Online False Discovery Rate Control

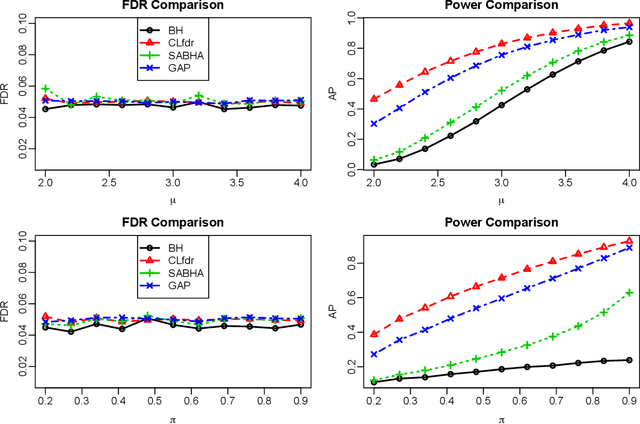
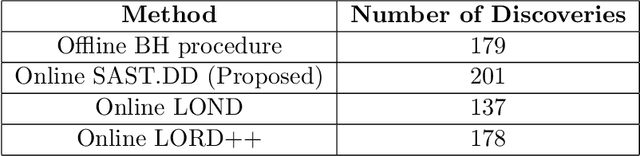
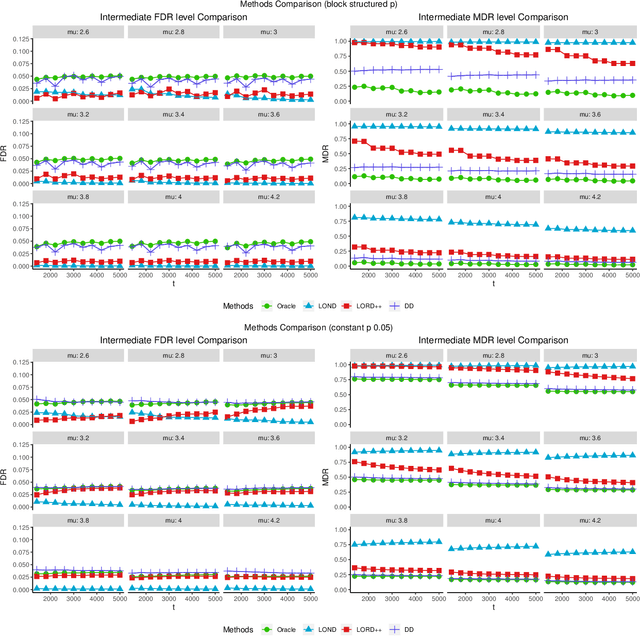
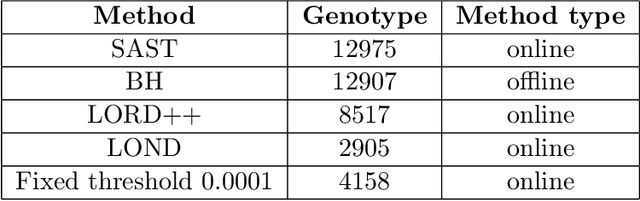
Consider the online testing of a stream of hypotheses where a real--time decision must be made before the next data point arrives. The error rate is required to be controlled at {all} decision points. Conventional \emph{simultaneous testing rules} are no longer applicable due to the more stringent error constraints and absence of future data. Moreover, the online decision--making process may come to a halt when the total error budget, or alpha--wealth, is exhausted. This work develops a new class of structure--adaptive sequential testing (SAST) rules for online false discover rate (FDR) control. A key element in our proposal is a new alpha--investment algorithm that precisely characterizes the gains and losses in sequential decision making. SAST captures time varying structures of the data stream, learns the optimal threshold adaptively in an ongoing manner and optimizes the alpha-wealth allocation across different time periods. We present theory and numerical results to show that the proposed method is valid for online FDR control and achieves substantial power gain over existing online testing rules.