GAEA: A Geolocation Aware Conversational Model

Image geolocalization, in which, traditionally, an AI model predicts the precise GPS coordinates of an image is a challenging task with many downstream applications. However, the user cannot utilize the model to further their knowledge other than the GPS coordinate; the model lacks an understanding of the location and the conversational ability to communicate with the user. In recent days, with tremendous progress of large multimodal models (LMMs) proprietary and open-source researchers have attempted to geolocalize images via LMMs. However, the issues remain unaddressed; beyond general tasks, for more specialized downstream tasks, one of which is geolocalization, LMMs struggle. In this work, we propose to solve this problem by introducing a conversational model GAEA that can provide information regarding the location of an image, as required by a user. No large-scale dataset enabling the training of such a model exists. Thus we propose a comprehensive dataset GAEA with 800K images and around 1.6M question answer pairs constructed by leveraging OpenStreetMap (OSM) attributes and geographical context clues. For quantitative evaluation, we propose a diverse benchmark comprising 4K image-text pairs to evaluate conversational capabilities equipped with diverse question types. We consider 11 state-of-the-art open-source and proprietary LMMs and demonstrate that GAEA significantly outperforms the best open-source model, LLaVA-OneVision by 25.69% and the best proprietary model, GPT-4o by 8.28%. Our dataset, model and codes are available

Kolmogorov-Arnold Attention: Is Learnable Attention Better For Vision Transformers?

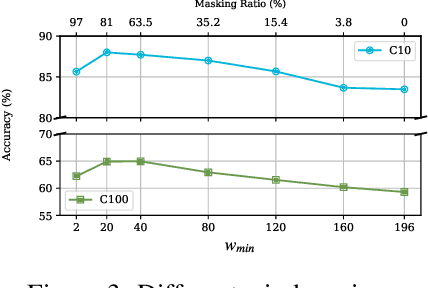
Kolmogorov-Arnold networks (KANs) are a remarkable innovation consisting of learnable activation functions with the potential to capture more complex relationships from data. Although KANs are useful in finding symbolic representations and continual learning of one-dimensional functions, their effectiveness in diverse machine learning (ML) tasks, such as vision, remains questionable. Presently, KANs are deployed by replacing multilayer perceptrons (MLPs) in deep network architectures, including advanced architectures such as vision Transformers (ViTs). In this paper, we are the first to design a general learnable Kolmogorov-Arnold Attention (KArAt) for vanilla ViTs that can operate on any choice of basis. However, the computing and memory costs of training them motivated us to propose a more modular version, and we designed particular learnable attention, called Fourier-KArAt. Fourier-KArAt and its variants either outperform their ViT counterparts or show comparable performance on CIFAR-10, CIFAR-100, and ImageNet-1K datasets. We dissect these architectures' performance and generalization capacity by analyzing their loss landscapes, weight distributions, optimizer path, attention visualization, and spectral behavior, and contrast them with vanilla ViTs. The goal of this paper is not to produce parameter- and compute-efficient attention, but to encourage the community to explore KANs in conjunction with more advanced architectures that require a careful understanding of learnable activations. Our open-source code and implementation details are available on: https://subhajitmaity.me/KArAt

Fibottention: Inceptive Visual Representation Learning with Diverse Attention Across Heads

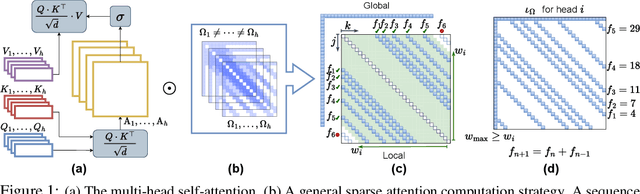
Visual perception tasks are predominantly solved by Vision Transformer (ViT) architectures, which, despite their effectiveness, encounter a computational bottleneck due to the quadratic complexity of computing self-attention. This inefficiency is largely due to the self-attention heads capturing redundant token interactions, reflecting inherent redundancy within visual data. Many works have aimed to reduce the computational complexity of self-attention in ViTs, leading to the development of efficient and sparse transformer architectures. In this paper, viewing through the efficiency lens, we realized that introducing any sparse self-attention strategy in ViTs can keep the computational overhead low. However, these strategies are sub-optimal as they often fail to capture fine-grained visual details. This observation leads us to propose a general, efficient, sparse architecture, named Fibottention, for approximating self-attention with superlinear complexity that is built upon Fibonacci sequences. The key strategies in Fibottention include: it excludes proximate tokens to reduce redundancy, employs structured sparsity by design to decrease computational demands, and incorporates inception-like diversity across attention heads. This diversity ensures the capture of complementary information through non-overlapping token interactions, optimizing both performance and resource utilization in ViTs for visual representation learning. We embed our Fibottention mechanism into multiple state-of-the-art transformer architectures dedicated to visual tasks. Leveraging only 2-6% of the elements in the self-attention heads, Fibottention in conjunction with ViT and its variants, consistently achieves significant performance boosts compared to standard ViTs in nine datasets across three domains $\unicode{x2013}$ image classification, video understanding, and robot learning tasks.

Towards Multi-modal Transformers in Federated Learning

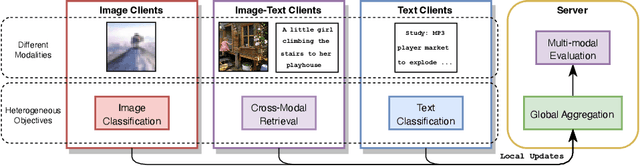
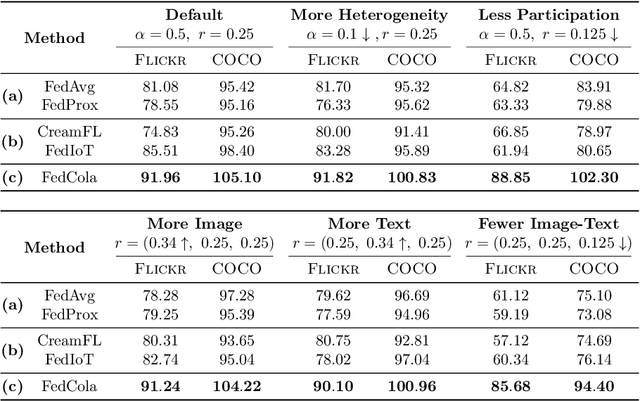
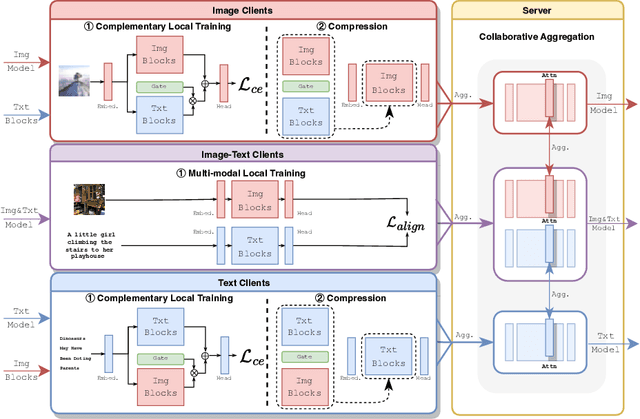
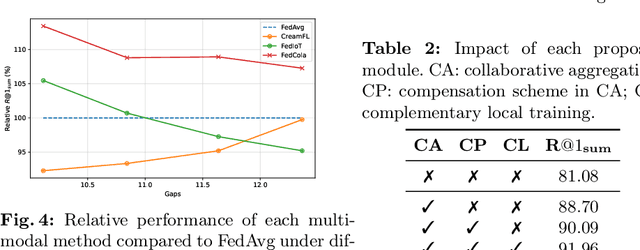
Multi-modal transformers mark significant progress in different domains, but siloed high-quality data hinders their further improvement. To remedy this, federated learning (FL) has emerged as a promising privacy-preserving paradigm for training models without direct access to the raw data held by different clients. Despite its potential, a considerable research direction regarding the unpaired uni-modal clients and the transformer architecture in FL remains unexplored. To fill this gap, this paper explores a transfer multi-modal federated learning (MFL) scenario within the vision-language domain, where clients possess data of various modalities distributed across different datasets. We systematically evaluate the performance of existing methods when a transformer architecture is utilized and introduce a novel framework called Federated modality complementary and collaboration (FedCola) by addressing the in-modality and cross-modality gaps among clients. Through extensive experiments across various FL settings, FedCola demonstrates superior performance over previous approaches, offering new perspectives on future federated training of multi-modal transformers.

Robust Multi-Modal Image Stitching for Improved Scene Understanding

Multi-modal image stitching can be a difficult feat. That's why, in this paper, we've devised a unique and comprehensive image-stitching pipeline that taps into OpenCV's stitching module. Our approach integrates feature-based matching, transformation estimation, and blending techniques to bring about panoramic views that are of top-tier quality - irrespective of lighting, scale or orientation differences between images. We've put our pipeline to the test with a varied dataset and found that it's very effective in enhancing scene understanding and finding real-world applications.

Multiview Aerial Visual Recognition (MAVREC): Can Multi-view Improve Aerial Visual Perception?

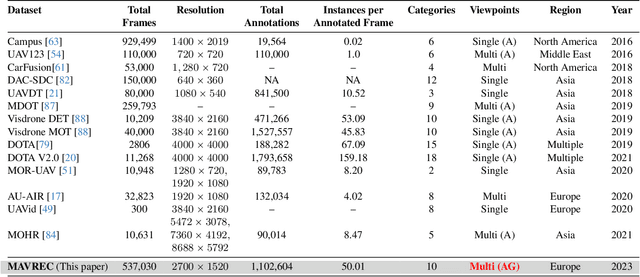
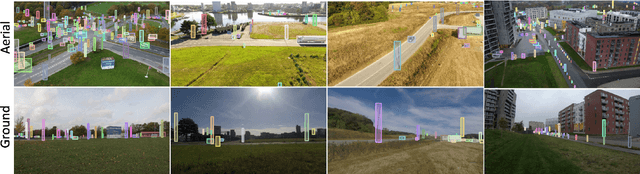
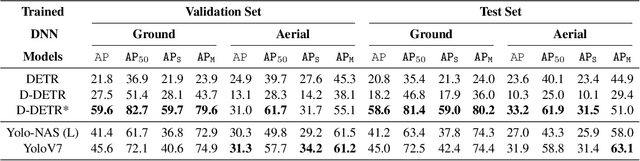
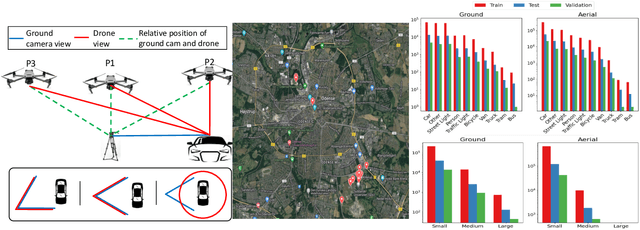
Despite the commercial abundance of UAVs, aerial data acquisition remains challenging, and the existing Asia and North America-centric open-source UAV datasets are small-scale or low-resolution and lack diversity in scene contextuality. Additionally, the color content of the scenes, solar-zenith angle, and population density of different geographies influence the data diversity. These two factors conjointly render suboptimal aerial-visual perception of the deep neural network (DNN) models trained primarily on the ground-view data, including the open-world foundational models. To pave the way for a transformative era of aerial detection, we present Multiview Aerial Visual RECognition or MAVREC, a video dataset where we record synchronized scenes from different perspectives -- ground camera and drone-mounted camera. MAVREC consists of around 2.5 hours of industry-standard 2.7K resolution video sequences, more than 0.5 million frames, and 1.1 million annotated bounding boxes. This makes MAVREC the largest ground and aerial-view dataset, and the fourth largest among all drone-based datasets across all modalities and tasks. Through our extensive benchmarking on MAVREC, we recognize that augmenting object detectors with ground-view images from the corresponding geographical location is a superior pre-training strategy for aerial detection. Building on this strategy, we benchmark MAVREC with a curriculum-based semi-supervised object detection approach that leverages labeled (ground and aerial) and unlabeled (only aerial) images to enhance the aerial detection. We publicly release the MAVREC dataset: https://mavrec.github.io.

Demystifying the Myths and Legends of Nonconvex Convergence of SGD

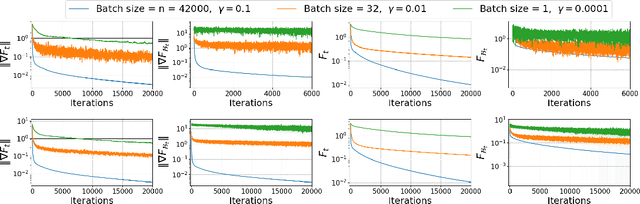
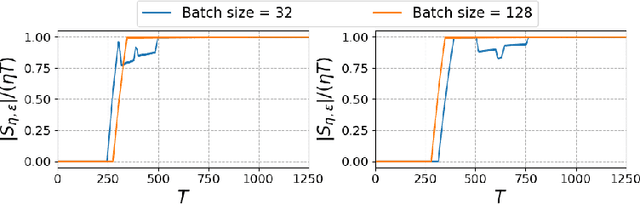
Stochastic gradient descent (SGD) and its variants are the main workhorses for solving large-scale optimization problems with nonconvex objective functions. Although the convergence of SGDs in the (strongly) convex case is well-understood, their convergence for nonconvex functions stands on weak mathematical foundations. Most existing studies on the nonconvex convergence of SGD show the complexity results based on either the minimum of the expected gradient norm or the functional sub-optimality gap (for functions with extra structural property) by searching the entire range of iterates. Hence the last iterations of SGDs do not necessarily maintain the same complexity guarantee. This paper shows that an $\epsilon$-stationary point exists in the final iterates of SGDs, given a large enough total iteration budget, $T$, not just anywhere in the entire range of iterates -- a much stronger result than the existing one. Additionally, our analyses allow us to measure the density of the $\epsilon$-stationary points in the final iterates of SGD, and we recover the classical $O(\frac{1}{\sqrt{T}})$ asymptotic rate under various existing assumptions on the objective function and the bounds on the stochastic gradient. As a result of our analyses, we addressed certain myths and legends related to the nonconvex convergence of SGD and posed some thought-provoking questions that could set new directions for research.

A Note on Randomized Kaczmarz Algorithm for Solving Doubly-Noisy Linear Systems

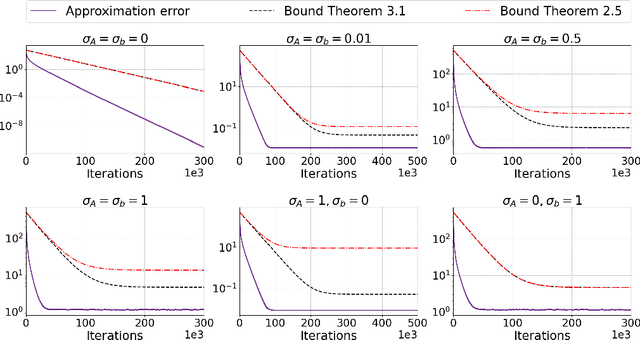
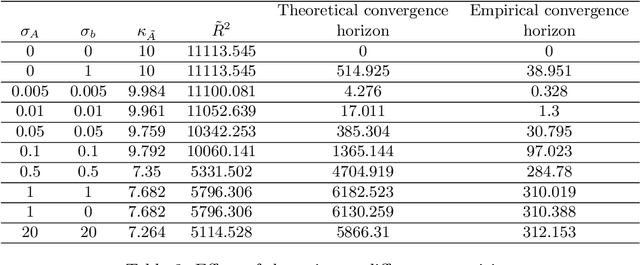
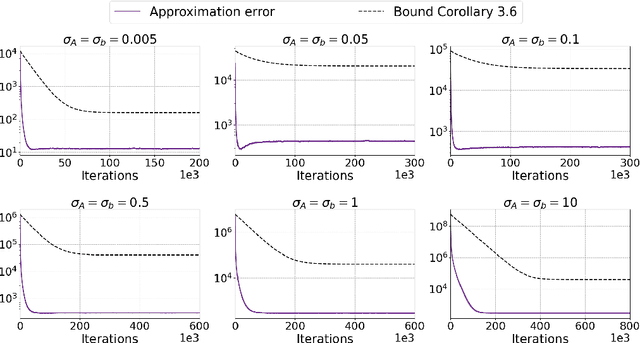
Large-scale linear systems, $Ax=b$, frequently arise in practice and demand effective iterative solvers. Often, these systems are noisy due to operational errors or faulty data-collection processes. In the past decade, the randomized Kaczmarz (RK) algorithm has been studied extensively as an efficient iterative solver for such systems. However, the convergence study of RK in the noisy regime is limited and considers measurement noise in the right-hand side vector, $b$. Unfortunately, in practice, that is not always the case; the coefficient matrix $A$ can also be noisy. In this paper, we analyze the convergence of RK for noisy linear systems when the coefficient matrix, $A$, is corrupted with both additive and multiplicative noise, along with the noisy vector, $b$. In our analyses, the quantity $\tilde R=\| \tilde A^{\dagger} \|_2^2 \|\tilde A \|_F^2$ influences the convergence of RK, where $\tilde A$ represents a noisy version of $A$. We claim that our analysis is robust and realistically applicable, as we do not require information about the noiseless coefficient matrix, $A$, and considering different conditions on noise, we can control the convergence of RK. We substantiate our theoretical findings by performing comprehensive numerical experiments.

Personalized Federated Learning with Communication Compression

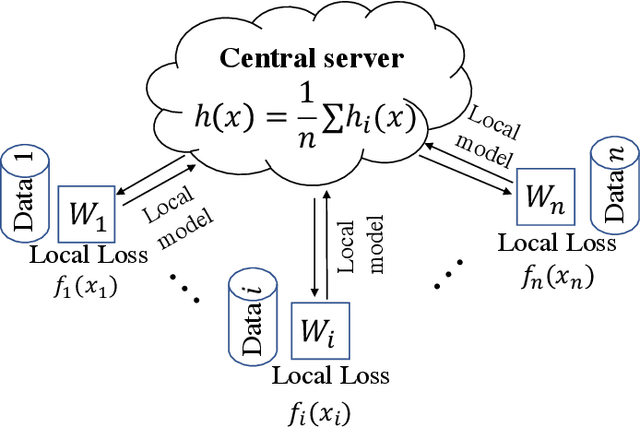
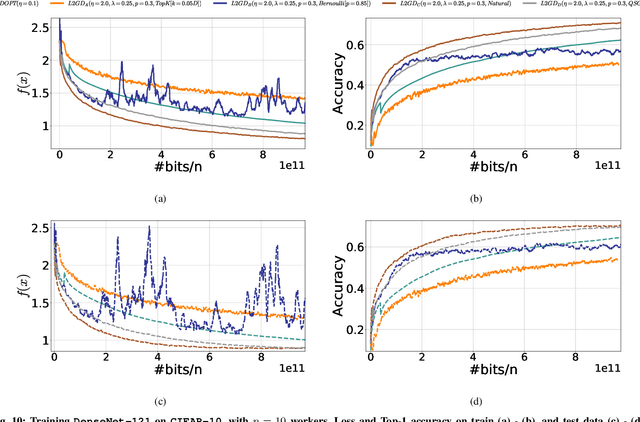
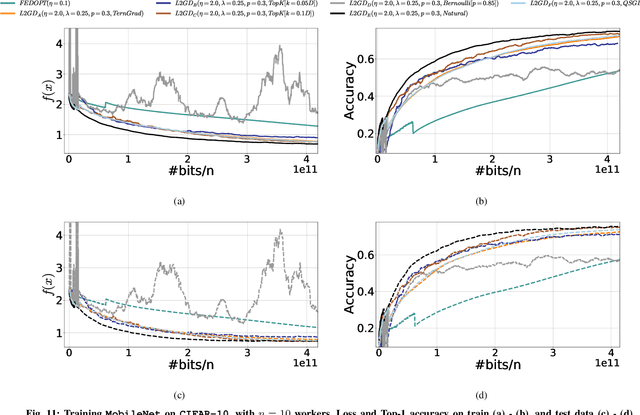
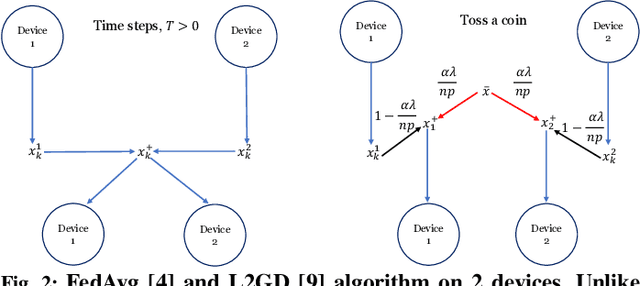
In contrast to training traditional machine learning (ML) models in data centers, federated learning (FL) trains ML models over local datasets contained on resource-constrained heterogeneous edge devices. Existing FL algorithms aim to learn a single global model for all participating devices, which may not be helpful to all devices participating in the training due to the heterogeneity of the data across the devices. Recently, Hanzely and Richt\'{a}rik (2020) proposed a new formulation for training personalized FL models aimed at balancing the trade-off between the traditional global model and the local models that could be trained by individual devices using their private data only. They derived a new algorithm, called Loopless Gradient Descent (L2GD), to solve it and showed that this algorithms leads to improved communication complexity guarantees in regimes when more personalization is required. In this paper, we equip their L2GD algorithm with a bidirectional compression mechanism to further reduce the communication bottleneck between the local devices and the server. Unlike other compression-based algorithms used in the FL-setting, our compressed L2GD algorithm operates on a probabilistic communication protocol, where communication does not happen on a fixed schedule. Moreover, our compressed L2GD algorithm maintains a similar convergence rate as vanilla SGD without compression. To empirically validate the efficiency of our algorithm, we perform diverse numerical experiments on both convex and non-convex problems and using various compression techniques.

Rethinking gradient sparsification as total error minimization

Gradient compression is a widely-established remedy to tackle the communication bottleneck in distributed training of large deep neural networks (DNNs). Under the error-feedback framework, Top-$k$ sparsification, sometimes with $k$ as little as $0.1\%$ of the gradient size, enables training to the same model quality as the uncompressed case for a similar iteration count. From the optimization perspective, we find that Top-$k$ is the communication-optimal sparsifier given a per-iteration $k$ element budget. We argue that to further the benefits of gradient sparsification, especially for DNNs, a different perspective is necessary -- one that moves from per-iteration optimality to consider optimality for the entire training. We identify that the total error -- the sum of the compression errors for all iterations -- encapsulates sparsification throughout training. Then, we propose a communication complexity model that minimizes the total error under a communication budget for the entire training. We find that the hard-threshold sparsifier, a variant of the Top-$k$ sparsifier with $k$ determined by a constant hard-threshold, is the optimal sparsifier for this model. Motivated by this, we provide convex and non-convex convergence analyses for the hard-threshold sparsifier with error-feedback. Unlike with Top-$k$ sparsifier, we show that hard-threshold has the same asymptotic convergence and linear speedup property as SGD in the convex case and has no impact on the data-heterogeneity in the non-convex case. Our diverse experiments on various DNNs and a logistic regression model demonstrated that the hard-threshold sparsifier is more communication-efficient than Top-$k$.