Exploring Pessimism and Optimism Dynamics in Deep Reinforcement Learning

Off-policy actor-critic algorithms have shown promise in deep reinforcement learning for continuous control tasks. Their success largely stems from leveraging pessimistic state-action value function updates, which effectively address function approximation errors and improve performance. However, such pessimism can lead to under-exploration, constraining the agent's ability to explore/refine its policies. Conversely, optimism can counteract under-exploration, but it also carries the risk of excessive risk-taking and poor convergence if not properly balanced. Based on these insights, we introduce Utility Soft Actor-Critic (USAC), a novel framework within the actor-critic paradigm that enables independent control over the degree of pessimism/optimism for both the actor and the critic via interpretable parameters. USAC adapts its exploration strategy based on the uncertainty of critics through a utility function that allows us to balance between pessimism and optimism separately. By going beyond binary choices of optimism and pessimism, USAC represents a significant step towards achieving balance within off-policy actor-critic algorithms. Our experiments across various continuous control problems show that the degree of pessimism or optimism depends on the nature of the task. Furthermore, we demonstrate that USAC can outperform state-of-the-art algorithms for appropriately configured pessimism/optimism parameters.

Probabilistic Actor-Critic: Learning to Explore with PAC-Bayes Uncertainty

We introduce Probabilistic Actor-Critic (PAC), a novel reinforcement learning algorithm with improved continuous control performance thanks to its ability to mitigate the exploration-exploitation trade-off. PAC achieves this by seamlessly integrating stochastic policies and critics, creating a dynamic synergy between the estimation of critic uncertainty and actor training. The key contribution of our PAC algorithm is that it explicitly models and infers epistemic uncertainty in the critic through Probably Approximately Correct-Bayesian (PAC-Bayes) analysis. This incorporation of critic uncertainty enables PAC to adapt its exploration strategy as it learns, guiding the actor's decision-making process. PAC compares favorably against fixed or pre-scheduled exploration schemes of the prior art. The synergy between stochastic policies and critics, guided by PAC-Bayes analysis, represents a fundamental step towards a more adaptive and effective exploration strategy in deep reinforcement learning. We report empirical evaluations demonstrating PAC's enhanced stability and improved performance over the state of the art in diverse continuous control problems.

Demystifying the Myths and Legends of Nonconvex Convergence of SGD

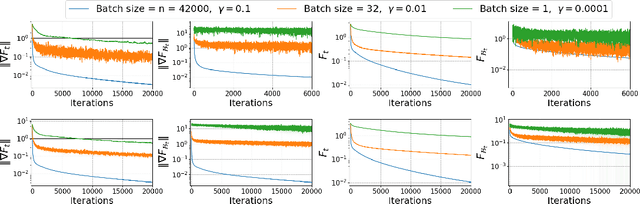
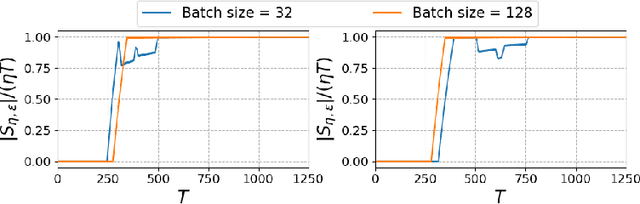
Stochastic gradient descent (SGD) and its variants are the main workhorses for solving large-scale optimization problems with nonconvex objective functions. Although the convergence of SGDs in the (strongly) convex case is well-understood, their convergence for nonconvex functions stands on weak mathematical foundations. Most existing studies on the nonconvex convergence of SGD show the complexity results based on either the minimum of the expected gradient norm or the functional sub-optimality gap (for functions with extra structural property) by searching the entire range of iterates. Hence the last iterations of SGDs do not necessarily maintain the same complexity guarantee. This paper shows that an $\epsilon$-stationary point exists in the final iterates of SGDs, given a large enough total iteration budget, $T$, not just anywhere in the entire range of iterates -- a much stronger result than the existing one. Additionally, our analyses allow us to measure the density of the $\epsilon$-stationary points in the final iterates of SGD, and we recover the classical $O(\frac{1}{\sqrt{T}})$ asymptotic rate under various existing assumptions on the objective function and the bounds on the stochastic gradient. As a result of our analyses, we addressed certain myths and legends related to the nonconvex convergence of SGD and posed some thought-provoking questions that could set new directions for research.

BOF-UCB: A Bayesian-Optimistic Frequentist Algorithm for Non-Stationary Contextual Bandits

We propose a novel Bayesian-Optimistic Frequentist Upper Confidence Bound (BOF-UCB) algorithm for stochastic contextual linear bandits in non-stationary environments. This unique combination of Bayesian and frequentist principles enhances adaptability and performance in dynamic settings. The BOF-UCB algorithm utilizes sequential Bayesian updates to infer the posterior distribution of the unknown regression parameter, and subsequently employs a frequentist approach to compute the Upper Confidence Bound (UCB) by maximizing the expected reward over the posterior distribution. We provide theoretical guarantees of BOF-UCB's performance and demonstrate its effectiveness in balancing exploration and exploitation on synthetic datasets and classical control tasks in a reinforcement learning setting. Our results show that BOF-UCB outperforms existing methods, making it a promising solution for sequential decision-making in non-stationary environments.

Learning from time-dependent streaming data with online stochastic algorithms

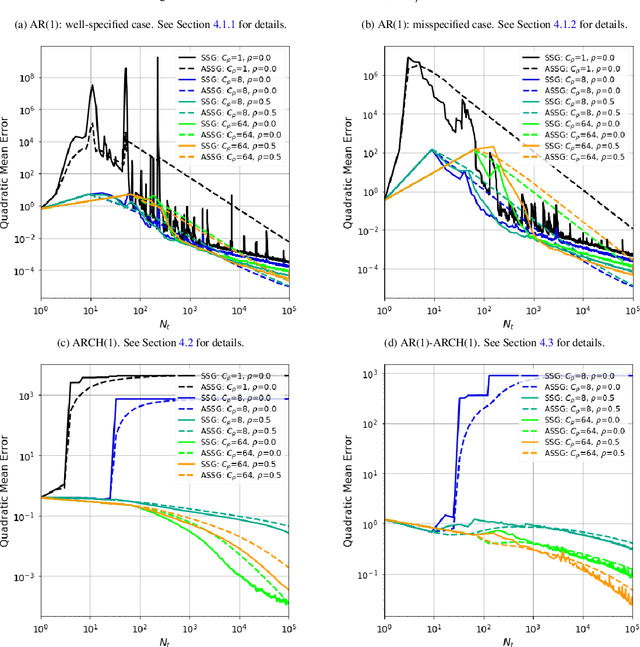
We study stochastic algorithms in a streaming framework, trained on samples coming from a dependent data source. In this streaming framework, we analyze the convergence of Stochastic Gradient (SG) methods in a non-asymptotic manner; this includes various SG methods such as the well-known stochastic gradient descent (i.e., Robbins-Monro algorithm), mini-batch SG methods, together with their averaged estimates (i.e., Polyak-Ruppert averaged). Our results form a heuristic by linking the level of dependency and convexity to the rest of the model parameters. This heuristic provides new insights into choosing the optimal learning rate, which can help increase the stability of SGbased methods; these investigations suggest large streaming batches with slow decaying learning rates for highly dependent data sources.

Non-Asymptotic Analysis of Stochastic Approximation Algorithms for Streaming Data

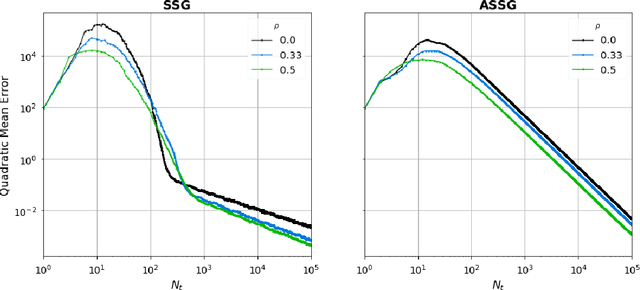
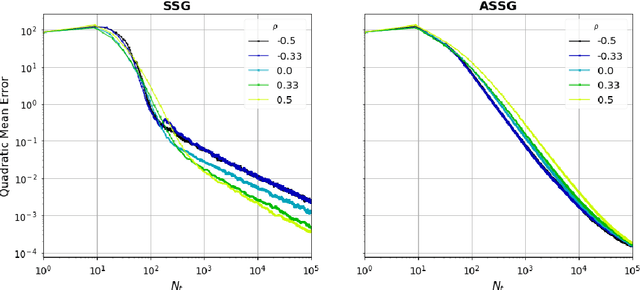
Motivated by the high-frequency data streams continuously generated, real-time learning is becoming increasingly important. These data streams should be processed sequentially with the property that the stream may change over time. In this streaming setting, we propose techniques for minimizing a convex objective through unbiased estimates of its gradients, commonly referred to as stochastic approximation problems. Our methods rely on stochastic approximation algorithms due to their computationally advantage as they only use the previous iterate as a parameter estimate. The reasoning includes iterate averaging that guarantees optimal statistical efficiency under classical conditions. Our non-asymptotic analysis shows accelerated convergence by selecting the learning rate according to the expected data streams. We show that the average estimate converges optimally and robustly to any data stream rate. In addition, noise reduction can be achieved by processing the data in a specific pattern, which is advantageous for large-scale machine learning. These theoretical results are illustrated for various data streams, showing the effectiveness of the proposed algorithms.

Predicting Risk-adjusted Returns using an Asset Independent Regime-switching Model

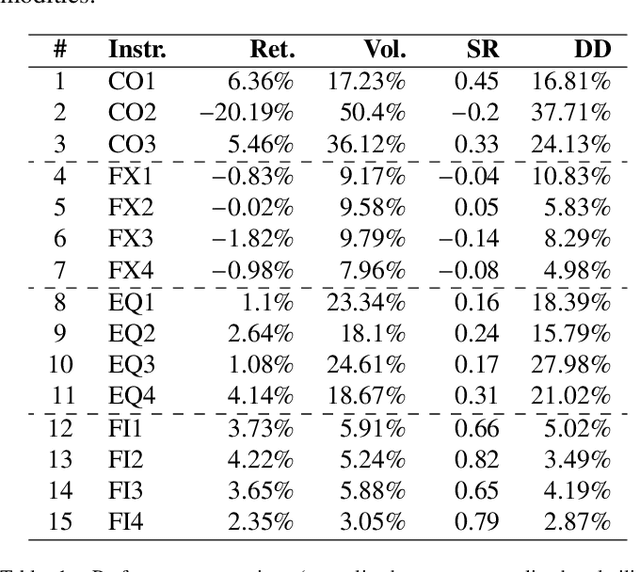
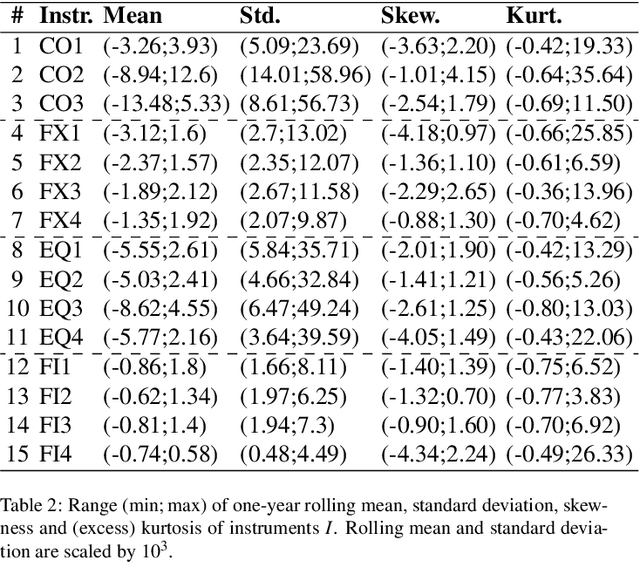
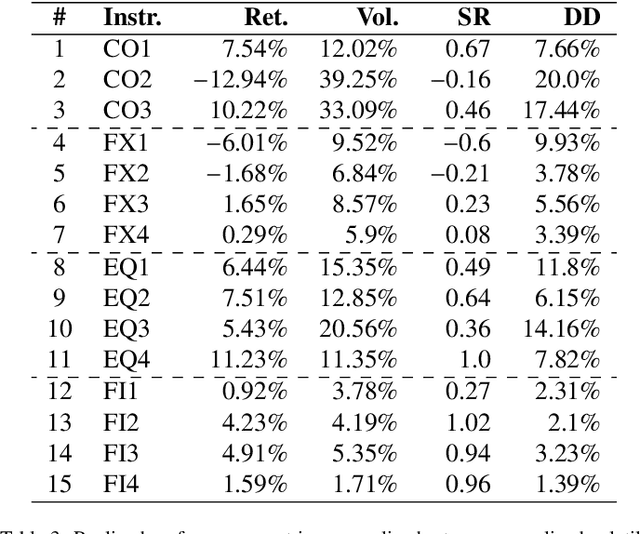
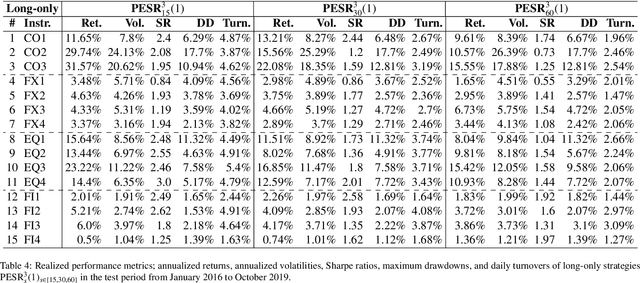
Financial markets tend to switch between various market regimes over time, making stationarity-based models unsustainable. We construct a regime-switching model independent of asset classes for risk-adjusted return predictions based on hidden Markov models. This framework can distinguish between market regimes in a wide range of financial markets such as the commodity, currency, stock, and fixed income market. The proposed method employs sticky features that directly affect the regime stickiness and thereby changing turnover levels. An investigation of our metric for risk-adjusted return predictions is conducted by analyzing daily financial market changes for almost twenty years. Empirical demonstrations of out-of-sample observations obtain an accurate detection of bull, bear, and high volatility periods, improving risk-adjusted returns while keeping a preferable turnover level.

An Adaptive Recursive Volatility Prediction Method

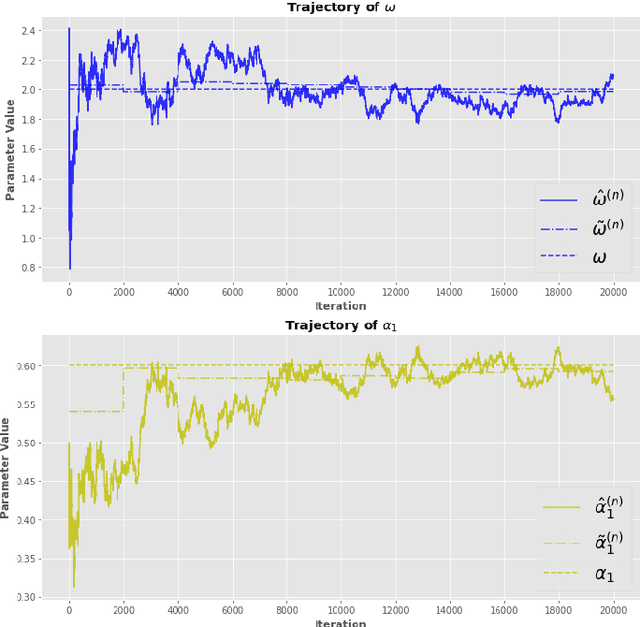
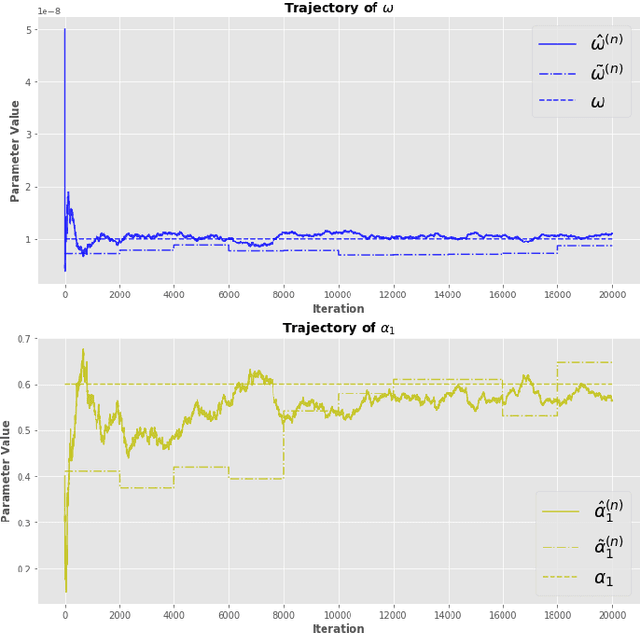
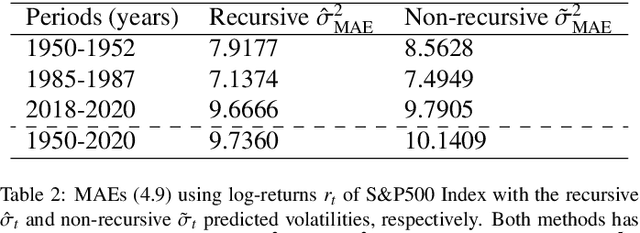
The Quasi-Maximum Likelihood (QML) procedure is widely used for statistical inference due to its robustness against overdisper-sion. However, while there are extensive references on non-recursive QML estimation, recursive QML estimation has attracted little attention until recently. In this paper, we investigate the convergence properties of the QML procedure in a general conditionally heteroscedastic time series model, extending the classical offline optimization routines to recursive approximation. We propose an adaptive recursive estimation routine for GARCH models using the technique of Variance Targeting Estimation (VTE) to alleviate the convergence difficulties encountered in the usual QML estimation. Finally, empirical results demonstrate a favorable trade-off between the ability to adapt to time-varying estimates and stability of the estimation routine.